噪声对相干衍射成像重构物体图像的影响

马子琦，刘 凯，潘子萌，廖 青

光学信息与模式识别湖北省重点实验室（武汉工程大学），湖北 武汉 430205

随着纳米技术的发展，人们对高分辨率成像有了迫切的需求。传统光学成像的分辨率受到透镜衍射极限的限制，为了突破透镜的衍射极限，相干衍射成像作为一种无透镜高分辨率成像方式应势而生。相干衍射成像（coherentdiffractiveimaging，CDI）是一种通过物体的远场衍射数据获得完整的光波场信息的无透镜成像方式，由于没有用到透镜，因此成像分辨率不受光学像差的限制，可以突破透镜的衍射极限［1-2］。自1999年华人学者Jianwei Miao首次通过实验验证了相干衍射成像以来［3-4］，超短光源和各种迭代算法的发展推动了相干衍射成像的快速发展和应用。相干衍射成像的核心问题是相位恢复问题，目前已经据此发展出多种相关的相位恢复算法，2004年Rodenburg等首次提出了叠层扫描相干衍射成像算法（ptychographic interactive engine，PIE），叠层扫描意指采用交叠式扫描，相邻的光斑扫描区域有大部分重叠，信息高度冗余，该算法极大的提高了数据的收敛速度［5］。2009年，Maiden和Rodenburg又拓展了PIE算法，使之可以在光探针信息未知的情况下恢复出目标函数的相位，该算法被称作扩展叠层迭代引擎（extended ptychographic iterative engine，ePIE）算法［6-8］。理想情况下相干衍射成像仅受到光源波长的限制，但在实际中，实验室可获得的数值孔径会受到噪声的限制，从而限制了可获得的分辨率［9-11］。

本文考虑用ePIE算法在MATLAB上重构物体图像，设置不同透射率的图像，在衍射过程中分别加入泊松噪声和高斯噪声来模拟实验，探究不同种类噪声对相干衍射成像重构不同透射率物体图像的影响。

1 叠层扫描相干衍射成像迭代算法重构物体图像

1.1 叠层扫描相干衍射成像迭代算法基本原理

叠层扫描相干衍射成像顾名思义就是在光探针扫描样本的过程中，光探针在物体上逐次移动，每次扫描到的区域与相邻扫描区域有大部分重叠。探测器依次记录每次扫描后的远场夫琅和费衍射图样，直到光探针遍历整个物体，然后通过迭代算法求出这些相互约束的衍射图样的共解，由于每次扫描的区域有大部分重叠，因此信息冗余度高，收敛速度快，可以快速得到所有扫描层的共解，重建出物体图像［12-13］。

图1中光源发出的相干光穿过小孔，提升相干性，随后移动光探针照射物体的不同位置，远场CCD相机记录一系列重叠的探针位置上的衍射图样，并通过叠层扫描迭代算法重构物体图像。

图1 叠层扫描相干衍射成像原理Fig.1 Principle of ptychography

在叠层扫描ePIE中，首先光探针函数用P（r）表示，物体函数用O（r）表示，光探针照射物体后的出射波函数用ψ表示：

j表示当前扫描位置，RS(j)表示该扫描处光探针与物体的相对位置矢量，根据标量衍射理论，出射波与到达探测器上的波函数是一个傅里叶变换的关系，因此对出射波函数进行一个快速傅里叶变换，就可以得到远场出射波函数的振幅和相位分布，将振幅替换成实验所测到的强度，保持相位不变，可以得到：

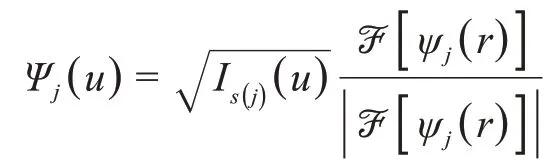
这样对频谱完成了一次修正，之后对Ψj(u)做逆傅里叶变换，得到更新后的出射波函数：

再利用更新后的出射波函数更新样本函数：

探针的更新方式与样本函数的更新类似：

这里更新后的样本函数作为下一次迭代时该位置的样本猜测函数，是光探针函数的共轭，α,β为调节因子，当光探针照射的所有位置都完成一次更新后，即完成了一次完整的迭代，重复迭代多次直到数据收敛至想要的结果，可以完成物体图像的重建［14］。

1.2 在MATLAB上用叠层成像恢复物体图像的结果

使用MATLAB编写生成衍射图像和ePIE算法，设定随机的高斯光作为光探针［15］，生成的高斯光场分布如图2（a）所示。光探针像素大小为64*64，移动步长为8，扫描区域像素大小为256*256，物体图像像素大小为128*128。每次迭代生成50张衍射图样作为ePIE算法的输入。

图2 （a）高斯光场分布；（b）图像Lena；（c）光探针叠层扫描交叠位置示意图Fig.2（a）Gaussian optical field distribution；（b）Image Lena；（c）Schematic diagram of overlapping positions of optical probe stack scanning

图3（a-f）中分别是迭代5次，10次，15次，20次，30次，50次的图像重建效果，可以看出迭代5次仅可得到图像的部分模糊信息；迭代10次可以重建图像的部分轮廓；迭代20次时图像轮廓明显，但图像细节不足；迭代30次时图像清晰，但强度不足；迭代50次已经达到十分清晰的效果，可以认为已正确重建该图像。整个迭代过程50次，在计算机上2 min即可完成。

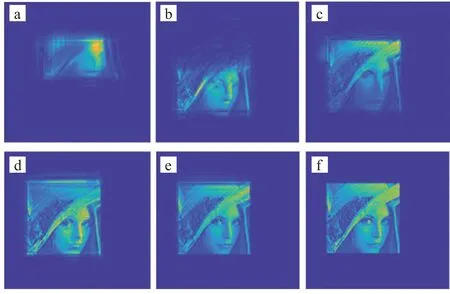
图3 不同迭代次数下图像Lena恢复效果：（a）5次，（b）10次，（c）15次，（d）20次，（e）30次，（f）50次Fig.3 Recovery effect of image Lena under different iterative times：（a）5 times，（b）10 times，（c）15 times，（d）20 times，（e）30 times，（f）50 times

物体的透射率表示了物体结构的透光性，透射率的大小会影响光透过样品后的远场衍射波。为了探究噪声对透射率不同的物体图像重构的影响，模拟中设置了像素大小为256*256的透射率不同的物体图像（见图4），该图像从左到右条纹透射率依次是100%，80%，50%，10%。图5表示不加噪声的情况下用ePIE算法对透射率物体图像进行重构的过程，随着迭代次数增加，重建图像逐渐清晰，其中5（d）是迭代50次之后重构出的图4中透射率物体图像的结果。

图4 透射率物体图像Fig.4 Transmissivities of object image

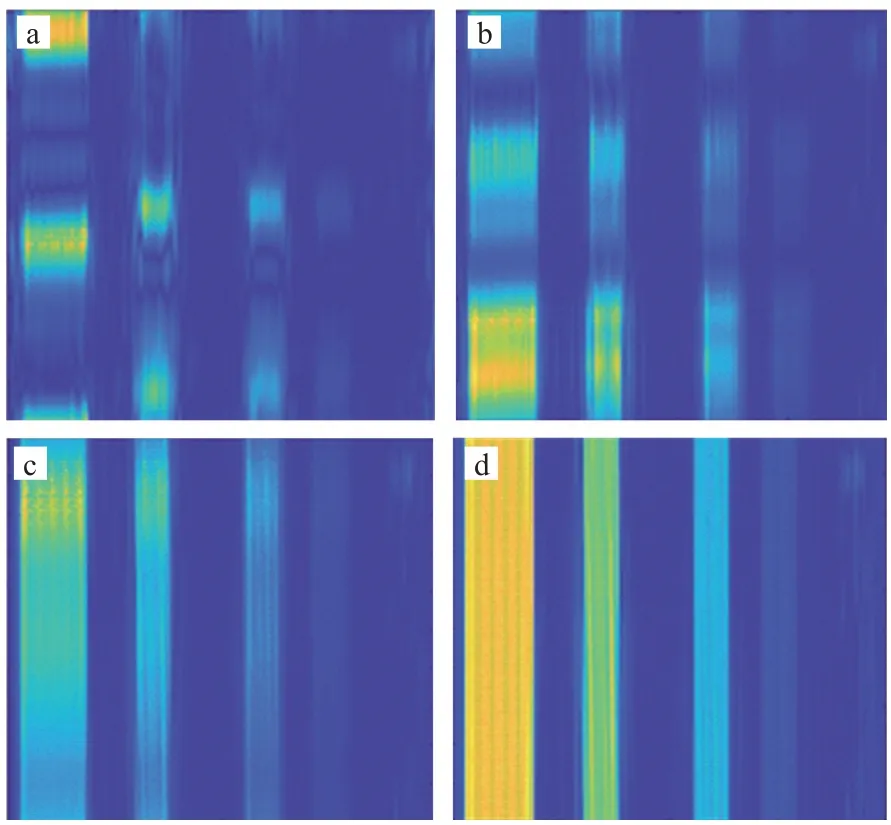
图5 透射率物体图像在不同迭代次数下的恢复效果：（a）5次，（b）10次，（c）30次，（d）50次Fig.5 Recovery effect of transmissivities of object image under different iterativetimes：（a）5 times，（b）10 times，（c）30 times，（d）50 times

2 噪声对恢复物体图像的影响

2.1 泊松噪声对物体图像恢复的影响

由于在相干衍射实验的过程中光子不是以均匀的方式到达探测器，而是以随机的方式到达，到达探测器表面的光子数目存在一定的波动，进而导致了图像的测量具有颗粒性，这个过程符合泊松分布，因此这种由测量的不确定性引起的噪声也称为泊松噪声［16-17］。

为了探究实验中泊松噪声对物体图像重建可能带来的影响，在图4中透射率物体图像的衍射图中加入泊松噪声，泊松噪声的大小与信号有关，且分布均值与方差相同，所以总光子数越多，均值越高，方差越大，在图像中定义信噪比（signal noise ratio，SNR）时将方差的平方根，即标准差定义为噪声，则当信号增加N倍时，标准差增加倍，噪声也增加倍，同时SNR增加倍。

以图6中（a）为例，加入依赖于初始信号的泊松噪声，其余条件与不加噪声的重构条件保持一致，计算出泊松噪声SNR为3.661。接下来信号每次扩大10倍，即SNR每次增加3.162倍，观察在叠层扫描相干衍射成像算法下迭代50次的重构过程：

图6（a-h）中分别表示SNR为3.661，6.823，9.985，13.147，16.309，19.741，22.633，25.795时的重建结果，图6（a）中可以看出SNR为3.661时噪声对不同透射率的图像重建影响均较大，无法重建物体图像，接下来每张图代表SNR增大 10倍的重建结果，图6（b）中SNR为6.823，透射率100%，80%，50%的物体图像恢复模糊，透射率10%的物体图像无法重建，图6（c）中SNR为9.985，透射率100%，80%，50%的物体图像轮廓已经逐渐清晰，但在这个SNR下透射率10%的物体图像仍然完全无法恢复；图6（d）中SNR为13.147，透射率100%，80%，50%的物体图像重建完成度增加，透射率10%的物体图像开始模糊地显现，但是无法明确分辨；图6（e）中SNR为16.309，除了透射率100%，80%，50%的物体图像更加清晰以外，强度也逐渐均匀，透射率10%的物体图像已经可以正确重建出来；图6（f-h）中，不同透射率的物体图像重建结果越来越清晰，边缘也越来越清晰，图像边缘线条与背景对比度明显，强度均匀。

2.2 高斯噪声对物体图像恢复的影响

在实验中，如果光探针的亮度不够均匀，或者探测器长时间工作后温度上升，就会产生高斯噪声，高斯噪声的概率密度函数服从正态分布，对物体图像模拟中的衍射图像加入不同SNR的高斯噪声，迭代50次的重构结果如图6所示。

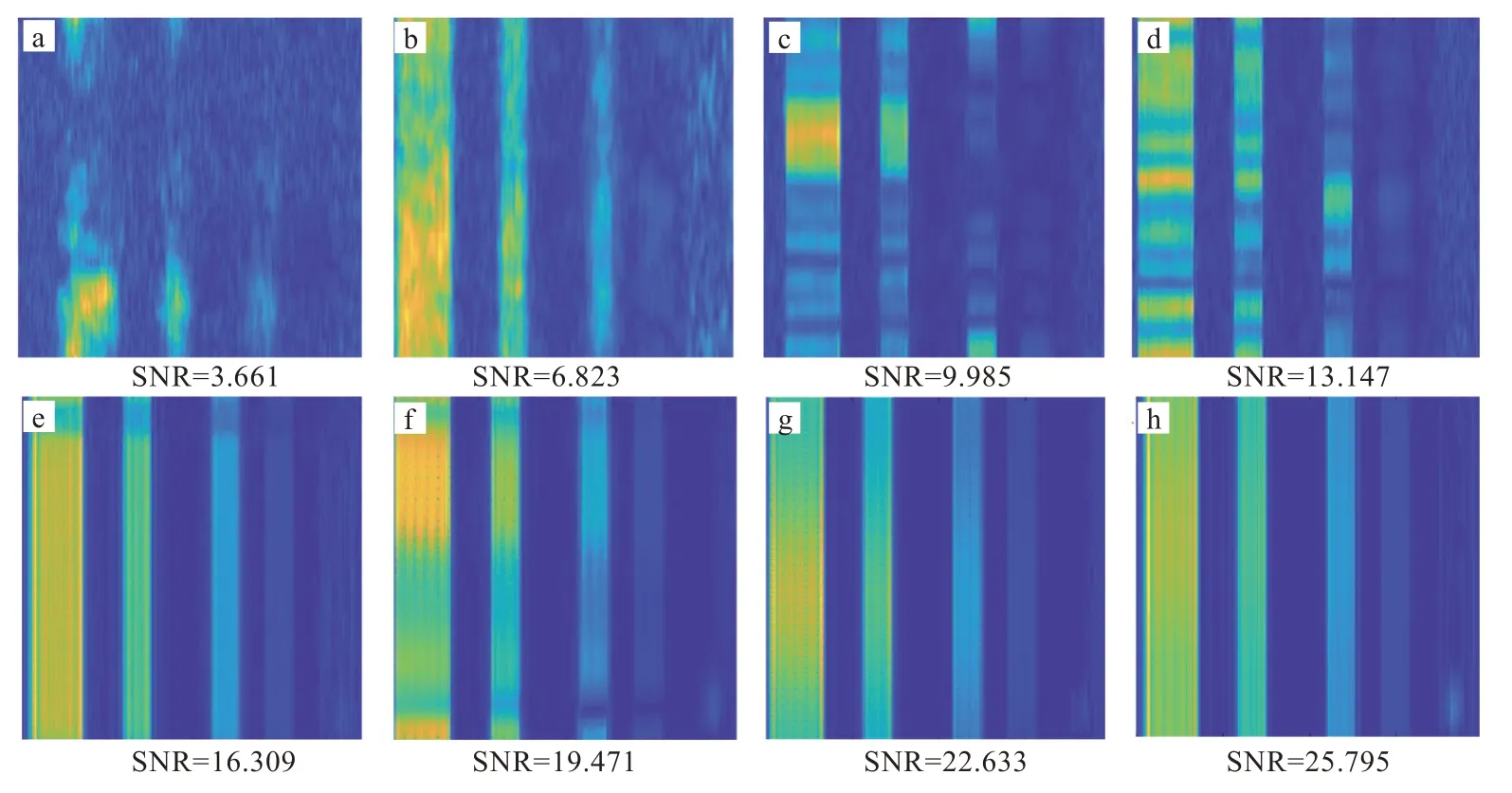
图6 泊松噪声对物体图像重建的影响Fig.6 Influence of Poisson noise on reconstruction of object image

图7（a-f）中表示SNR为1，3，5，8，10，12，14，16，18，20，22，24时的重建结果，从图7（a）中可以看出，SNR为1时，可以看出噪声很明显，几乎无法分辨样本，图7（b）中SNR为3，透射率为10%的物体图像完全不显示，透射率为100%，80%，50%的物体图像模糊无法分辨，图7（c-e）中SNR为5，8，10时仍然是无法看到透射率10%的物体图像，但是透射率100%，80%，50%的物体图像轮廓渐渐清晰，但并不能完全重建出物体图像，图7（f）中SNR为12，物体图像条纹边缘有明显噪声，透射率100%，80%，50%的物体图像基本可以重建出来，10%的物体图像不是很容易分辨；图7（g-i）中SNR为14，16，18，虽然物体图像的条纹边缘仍有噪声，但透射率为100%，80%，50%，10%的物体图像都可以重建出来，只是透射率10%的物体图像比较暗；图7（j）中，SNR提高到20时，不同透射率的物体图像皆清晰可见，但条纹边缘会有伪影；图7（kl）中SNR为22和24，不同透射率的物体图像均重建良好，且边缘十分清晰，噪声已经基本对重建没有影响。

图7 高斯噪声对物体图像重建的影响Fig.7 Influence of Gaussian noise on reconstruction of object image

3 结果与分析

在叠层扫描相干衍射成像的基础上，编写程序生成物体图像的衍射图，并利用ePIE算法模拟验证了物体图像的重建情况，之后在不同透射率的物体图像衍射图中分别加入了泊松噪声和高斯噪声进行重构。

具体重构结果表明低SNR的泊松噪声对透射率不同的物体图像重构影响均很大，对透射率低的物体图像的影响比对透射率高的物体图像影响要大，当SNR较低时，透射率10%的物体图像不能重构。SNR为3.661时，添加了泊松噪声的初始信号无法重构图像；信号强度增加103倍时，即SNR为13.147时，透射率100%，80%的物体图像轮廓可以重建出来，透射率50%的物体图像重构不完整，透射率10%的物体图像无法重构，信号强度增加104倍时，SNR为16.309时，泊松噪声对透射率100%，80%，50%的物体图像影响已经不大，所以如果物体图像整体透射率大于50%，在这个SNR的情况下已经可以恢复良好，若图像透射率较低，则在实验中需要再增加信号强度。

在衍射图中加入高斯噪声时，SNR低于8时对透射率50%和10%的物体图像影响较大，SNR为8到10时，对透射率为100%，80%，50%的物体图像有较大影响，但是影响效果差异不大，对透射率10%的物体图像影响最大，无法重构透射率10%的物体图像，SNR达到12时，尽管图像周围仍有噪声造成的伪影，但已经可以完全区分出不同透射率的物体图像，随着SNR增加到24，重建的图像噪声减小，边缘清晰，强度均匀，当SNR达到22和24时，图像重构效果非常好，噪声对物体图像的重构几乎已经没有影响。

图8为根据2.1节和2.2节的研究内容绘制的透射率的最低恢复程度和SNR之间的关系，黑色实线表示泊松噪声SNR为6.823时，仅能恢复透射率100%的物体图像，SNR为9.985时，可以恢复透射率80%的物体图像，SNR为16.309时。可以恢复透射率低于50%的物体图像。SNR为22.663时，可以恢复透射率低至10%的物体图像；红色实线表示高斯噪声SNR为12时，仅可恢复透射率100%的物体图像，SNR为16时，可以恢复透射率80%的物体图像，SNR为18时。可以恢复透射率低于50%的物体图像。SNR为22时，可以恢复透射率低至10%的物体图像。

图8 物体图像重构效果与其透射率和SNR的关系Fig.8 Relation between reconstruction effect of object image and its transmissivities and signal-to-noise ratio

在实验测量中，物体的密度结构通常不是均匀的，因此不同密度的细节对光的透射率也不同。对物体进行重构时，物体透射率低的部分更容易受到噪声影响。研究噪声对不同透射率物体图像的重构影响，就可以重构物体结构。

4 结 论

本文在衍射成像模拟中选取了测量中会遇到的两种典型的噪声：泊松噪声和高斯噪声，根据噪声与噪声影响的定量关系探究了两种噪声对相干衍射成像中重构透射率物体图像的影响，探究结果表明噪声对透射率低的物体图像影响更大，SNR低于6时无法重构物体图像，SNR大于22时噪声对不同透射率物体图像的重构均不再有影响。为相干衍射成像的实际应用提供了理论指导。