基于改进传播算子的双基地多输入多输出雷达参数估计

王家珂，吴云韬*，巩朋成

1.智能机器人湖北省重点实验室（武汉工程大学），湖北 武汉 430205；2.武汉工程大学计算机科学与工程学院，湖北 武汉 430205

受启发于通信领域中的多输入多输出系统，Fisher等人首次提出将多输入多输出（multipleinput multiple-output，MIMO）技术引入到雷达系统，从而构建出一种全新的雷达体制即MIMO雷达。MIMO雷达通过发射端同时发射出多个相互正交的信号，在接收端经过匹配滤波处理，分离出各个发射信号，获得了更大的虚拟孔径，提高了雷达系统的性能。MIMO雷达在参数估计、目标检测、杂波抑制等［1-3］方面相较于传统雷达优势显著，因此成为雷达研究的热点。

MIMO雷达按照发射阵和接收阵的设置方式可以分为单基地MIMO雷达和双基地MIMO雷达。双基地MIMO雷达的回波信号中包含了目标相对于发射阵和接收阵的角度信息，因此可以对目标进行交叉定位。在双基地MIMO雷达的波离方向（direction of departure，DOD）和 波 达 方 向（direction of arrival，DOA）联合估计问题中，文献［4］研究了基础多重信号分类（multiple signal classification，MUSIC）算法估计MIMO雷达方位角的问题，该方法需要进行二维谱峰搜索，因此计算量较大。文献［5］则提出了一种降维MUSIC算法，该算法利用凸优化的方法，将传统二维MUSIC算法中的二维谱峰搜索转化为两个一维谱峰搜索，降低了算法的运算量。文献［6］将求根MUSIC算法应用于MIMO雷达，避免了因谱峰搜索产生的巨大计算量。文献［7］在求根MUSIC算法基础上，增加了酉变换处理，进一步降低了算法的运算量。文献［8］和文献［9］基于均匀线阵的结构，利用其具有的旋转不变性，运用旋转不变子空间（estimation of signal parameters via rotational invariance technique，ESPRIT）算法估计出目标的方位角，文献［9］中ESPRIT算法实现了目标方位角的自动配对。文献［10］提出酉ESPRIT算法，通过前后向平滑技术［11］，将接收阵接收到的信号从复数域转换到实数域，有效地降低了运算量，并且估计精度有所提高。文献［12］结合MUSIC算法和ESPRIT算法的优点，提出了ESPRIT-MUSIC算法。文献［13］提出一种改进的传播算子（propagator method，PM）算法，在估计精度接近传统算法的同时，降低了运算量。文献［14］基于MIMO雷达输出信号的张量模型，提出一种多维奇异值分解算法，该算法充分利用多维结构，因此估计精度较传统算法更高。

本文提出一种运用于双基地MIMO雷达方位角估计的改进的PM方法，根据传播算子［15］定义要求，提取存在旋转不变结构的数据求得协方差，组合相关数据矩阵，使用前后向平滑方法求得传播算子，根据其内部结构特征求出旋转不变因子，估计出DOD和DOA的值，从而实现双基地MIMO雷达DOD和DOA的联合估计。

1 信号模型

在双基地MIMO雷达系统结构中，假设其发射阵和接收阵分别为m个阵元和n个阵元的均匀线阵，阵元间距均为d=λ/2，λ为波长，发射阵同时发射m个正交信号S∈[s1,s2,...,s m]T∈ℂm×L，L代表单个脉冲内的采样点数，由于各信号之间彼此相互正交，因此存在等式SSH/L=I m。假设存在K个远场目标，则第k个目标的DOD和DOA可分别用θk和φk来表示。则接收阵列接收到的第q个脉冲信号用矩阵形式表示为

式中，A t=[a t(θ1),a t(θ2),...,a t(θK)]和A r=[a r(φ1),a r(φ2),...,a r(φK)]分别为发射阵和接收阵的导向矩阵，其 中a t(θk)=[1,ej2πdsinθk/λ,...,ej2π(m-1)dsinθk/λ]T为 第k个 目 标 发 射 导 向 矢 量 ，a r(φk)=[1,ej2πdsinφk/λ,...,ej2π(n-1)dsinφk/λ]T为第k个目标接收导向矢量。Λq=diag(c q)，其中，c q=[α1,q,α2,q,...,αK,q]T，αk,q表示第k个目标在第q个脉冲时目标的反射系数，N q是均值为零的高斯白噪声矩阵。将X q右乘SHL进行匹配滤波，并将结果向量化以增加虚拟阵列孔径，最后将Q个脉冲信号排列成一个mn×Q维信号矩阵可得

式中，⊙表示Khatri-Rao积，C=[c1,c2,...,c Q]，N表示匹配滤波过后的高斯白噪声矩阵。

2 改进的PM方法

观察双基地MIMO雷达匹配滤波输出的信号矩阵Y，用选择矩阵选择前(m-1)n个阵元和后(m-1)n个阵元输出数据，分别记为Y1和Y2，用选择矩阵选择前m(n-1)个阵元和后m(n-1)个阵元输出数据，分别记为Y3和Y4，则有

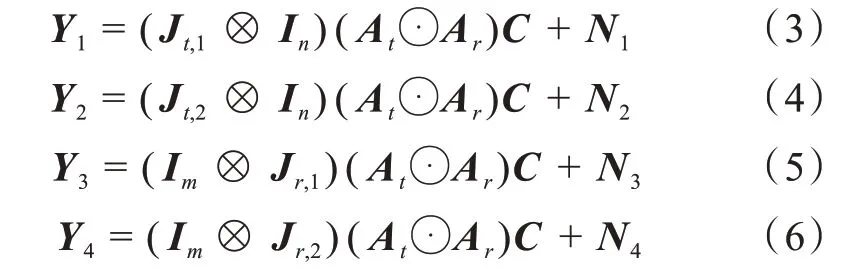
其 中，J t,1=[I m-1,0]，J t,2=[0,I m-1]，J r,1=[I n-1,0]及J r,2=[0,I n-1]为选择矩阵，I为单位矩阵，0表示零 向 量 。 由 式（3）和 式（4）得(J t,2⊗I n)(A t⊙A r)=(J t,1⊗I n)(A t⊙A r)Φt，其 中Φt= diag(ej2πdsinθ1/λ,ej2πdsinθ2/λ,...,ej2πdsinθK/λ)，由 式（5）和式（6）得(I m⊗J r,2)(A t⊙A r)=(I m⊗J r,1)(A t⊙A r)Φr，其中Φr=diag(ej2πdsinφ1/λ,ej2πdsinφ2/λ,...,ej2πdsinφK/λ)。

对数据矩阵Y1和Y2进行处理，假设(J t,1⊗I n)(A t⊙A r)=A，则存在(J t,2⊗I n)(A t⊙A r)=AΦt，首先根据传播算子的定义有B=[AT(AΦt)T]T，矩阵A可以被分解为A=[AT1AT2]T，其中A1表示矩阵A的前K行，A2表示矩阵A的第K+1到(m-1)n行。同样，可以把B分解为B=[AT1BT2]T，其中B2由B的第K+1到2(m-1)n行组成。假设A1是非奇异的，传播算子P可以被定义为一个唯一的线性算子形式

其中，H表示共轭转置。

以Y1和Y2为例，将选择矩阵处理过后的数据矩阵组合表示为得到样本协方差矩阵R=ZZH/Q，并对其进行前后向平滑处理可得R fb=(R+JR*J)/2，其中J为大小为2(m-1)n的反对称矩阵，将R fb分解为

其中，R1和R2分别表示R fb的前K列和后2(m-1)n-K列，基于样本协方差矩阵的传播算子的最小二乘解可以表示为

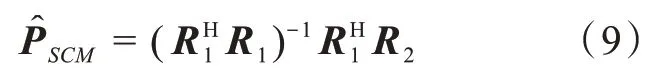
从A和B的分解形式可得

另一方面，可以将的共轭转置矩阵分解为

其中，A2,A1Φt,A2Φt的维度与的维度一一对应。根据式（7）对比式（10）和式（11），可以得到

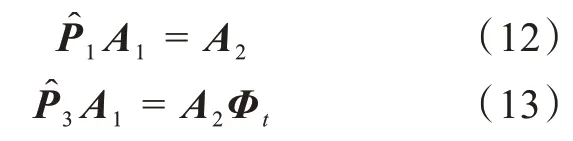
由式（12）可得

其中，#表示伪逆，将式（14）带入式（13）中可得

式（15）表明矩阵Φt的对角线上元素的估计值可以由的k个特征值得到，相应的特征值分解可得

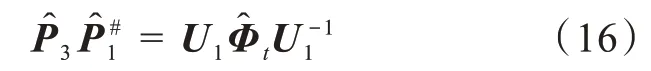
其中，diag(λ1,λ2,…,λk)为Φt的估计值，因此DOD的估计值可以表示为

给定另一个传播算子V，处理数据Y3和Y4，重复上述步骤得到，从而得到diag(v1,v2,…,vk)，DOA的估计值表示为

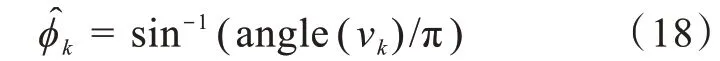
由于DOD和DOA是分开估计的，使用最大似然估计法对其进行配对，得到正确的方位角估计结果。

3 仿真实验

采用仿真实验将所提出方法与文献［16］中传统ESPRIT算法和PM算法进行对比，通过3组仿真实验来验证所提出方法的有效性。考虑一个发射阵和接收阵均为等距线阵的双基地MIMO雷达系统，阵元间距为半波长，假设远场存在两个目标，它们相对于发射阵和接收阵的方位角分别为(θ1,φ1)=(10°,15°)，(θ2,φ2)=(25°,35°)，500次蒙特卡洛仿真的均方根误差定义为RMSE=其中，和分别表示目标DOD方位角的θk和DOA方位角的φk在第l次蒙特卡洛实验中的估计值。

图1是利用本文所提出方法在发射阵元数m=10，接收阵元数n=10，信噪比为10 dB，脉冲数Q=50时进行100次蒙特卡洛实验目标定位的结果。由图1可以看出，本文所提出方法能有效估计出多目标二维方位角。

图1 改进方法目标定位结果Fig.1 Target location results of improved method

图2显示了本文所提出方法与传统ESPRIT算法和PM算法目标估计均方根误差随信噪比变化关系。实验中，发射阵元数和接收阵元数分别为m=10，n=10，脉冲数Q=50。从图2可看出，随着信噪比的增加，各算法性能均有提升，与ESPRIT算法和PM算法相比，本文所提出方法估计精度更高，并且与传统PM算法相比，在低信噪比情况下本文所提出方法更加稳定。

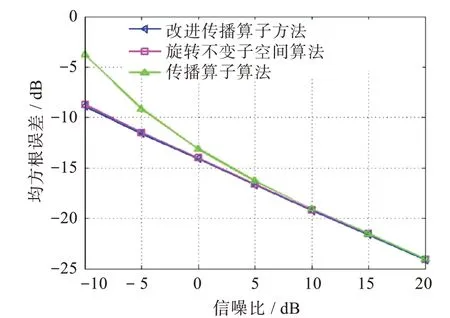
图2 目标估计均方根误差随信噪比变化关系Fig.2 Root mean square error of target estimation versus signal to noise ratio

图3显示了本文所提出方法与传统ESPRIT算法和PM算法目标估计均方根误差随脉冲数变化关系。实验中阵元数m=10，n=10，信噪比为5dB。从图3可看出，随着脉冲数Q的增加，各算法估计精度均有提高，且本文所提出方法较ESPRIT算法和PM算法，估计性能更好。

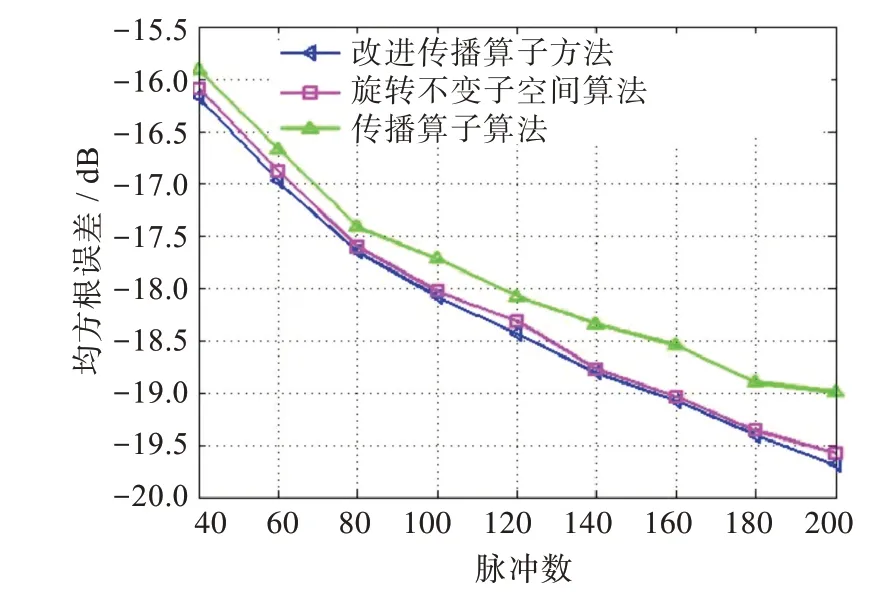
图3 目标估计均方根误差随脉冲数变化关系Fig.3 Root mean square error of target estimation versus number of pulse

4 结 论

以上阐述了一种基于改进PM算法的双基地MIMO雷达方位角估计方法。该方法根据传播算子定义要求提取存在旋转不变结构的相关数据，组合相关数据求得协方差，采用前后向平滑方法求得传播算子，根据其内部结构特征求出旋转不变因子，估计出DOD和DOA的值。该方法较传统ESPRIT算法和PM算法具有更好的估计性能，并且在低信噪比情况下与传统PM算法相比性能更加稳定，仿真实验表明该方法在方位角估计精度上有所提高。