随机谣言传播模型的建立与动态分析

石星星， 叶海平

(东华大学 理学院， 上海 201620)

谣言作为一种典型的社会现象，其传播手段、传播途径不断变化。随着科技的进步和互联网的快速发展，人们获取信息的途径也发生了巨大的变化。一个事件的发生，几分钟内就可能获得大量人的关注和传播。这使人们能及时地获取大量的信息，但对谣言的传播也产生巨大的影响。例如，2011年的“抢盐事件”，2012年的“世界末日”引起的抢购热，“肉毒杆菌”事件造成企业近200亿的营业损失，以及“6翅膀8腿怪鸡”的谣言让人闻鸡变色。此类谣言不仅造成了一定的社会恐慌，也对企业和个人产生很大的影响，因此研究谣言传播有较大的现实意义。

谣言在人群中的传播扩散与病毒的传播相似，因此现有的谣言模型大多借鉴了传染病模型，但是，鉴于描述谣言实际传播过程的增长和衰变的原理及假设条件的不同，有很多种不同的建模方法。在经典的Daley-kendall谣言传播模型[1]中，Daley等第一次将模型中的个体分为3类：未听过谣言者(Ignorants)、传播谣言者(Spreads)以及不传播谣言者(Stiflers)，并类比Kermack-McKendrick 传染病的讨论方法发展了随机谣言传播模型(D-K模型)。Maki等[2]认为谣言在传播者和其他人之间的传播是双向的，因此引入Maki-Thompson模型来描述基于马尔可夫链的谣言传播。

随着研究的深入，由于谣言传播的途径及受影响因素与传染病的传播存在差异，研究者考虑了人们第一次听到谣言时的心理反应、个人的受教育程度，以及外界干预(政府、媒体等)对谣言传播的影响，从而建立了不同的谣言传播模型。对于常微分方程模型，陈华[3]讨论了一类具有媒体播报效应的谣言传播模型，通过对该模型的稳定性分析表明媒体报道在谣言传播中的影响。文献[4]根据人们对谣言的不同态度进行分析，建立了SHIR模型，并讨论了该模型在平衡点处的稳定性。Zhao等[5]根据已知谣言者的不同行为，在偏微分方程的基础上提出了一种新的SIS谣言传播模型，讨论了该模型解的存在唯一性，并分析了解的稳定性。文献[6]分别对有年龄结构和无年龄结构下的谣言传播模型进行讨论。

Zanette[7]研究了交互规则对谣言传播效率和可信度的影响，把谣言传播放到社交网络中进行讨论分析。文献[8]在SIR模型的基础上，引入噪声干扰，利用随机微分方程讨论均匀网络和异质网络的谣言扩散动力学。一些学者认为谣言的传播具有潜伏期，而且对于一个社交圈来说并不是固定不变的，因此对这些情况研究建立了SCIR模型，并做出稳定性分析[9]。

传染病模型的研究[10-13]表明，环境噪声对其传播有很大的影响，那么类似的环境噪声对谣言的传播也存在影响。Jia等[14]根据文献[15]的研究，在谣言传播模型中引入白噪声，一种直接与S(t)和I(t)成比例的随机扰动，建立了如下模型：

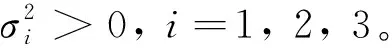
1 随机谣言传播模型的建立

文献[18]研究了谣言传播的确定性模型为

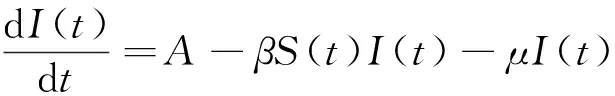
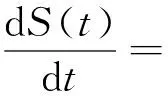
R(t))-μS(t)

式中：I(t)为谣言未知者；S(t)为谣言传播者；R(t)为谣言沉默者, 个体以常数A进入该群体并成为未知者；μ、β分别为迁入率和传播率；τ为未知者从第一次听到谣言到传播谣言的潜伏期；γ为沉默率, 即谣言传播者与谣言传播者或沉默者接触后成为沉默者的概率.

根据Laarabi等[18]的建模思想，本文假设其中未听过谣言者从第一次听到谣言到传播谣言的潜伏期τ=0，并加入遗忘机制建立SIRS谣言传播模型。在本文的研究中将模型中的人群分为以下3类：S(t)为从未听过谣言者，即谣言易感者；I(t)为听过谣言并且传播谣言者，即谣言传播者；R(t)为听过谣言但不传播谣言者，即谣言免疫者。

由于现实中人行为的复杂性及人际关系的多变性，一个人的社交圈并不是恒定不变的，本研究假设个体以一定概率B进入该社交圈并成为谣言易感者，每类人群以概率μi(i=1, 2, 3)移出该类人群。当谣言易感者与谣言传播者接触，谣言易感者变为谣言传播者的概率为β。当谣言传播者与谣言传播者以及谣言免疫者接触，经过信息对比和综合判断，谣言传播者变为谣言免疫者的概率为γ。由于时间关系和新谣言的传播，谣言免疫者遗忘此谣言变为谣言易感者的概率为δ。

综上可以建立一个确定性的SIRS微分方程模型如式(1)所示。

dS(t)=(B-βS(t)I(t)-μS(t)+δR(t))dt

dI(t)=(βS(t)I(t))-γI(t)(I(t)+R(t))-

μI(t))dt

dR(t)=(γI(t)(I(t)+R(t))-(μ+δ)R(t))dt

(1)

式中：B,β,γ,δ,μ都是正数；S(0)>0,I(0)>0,R(0)>0。

该模型的基本再生数为

dS(t)=(B-βS(t)I(t)-μS(t)+

δR(t))dt+σ1S(t)dB1(t)

dI(t)=(βS(t)I(t)-γI(t)(I(t)+R(t))-

μI(t))dt+σ2I(t)dB2(t)

dR(t)=(γI(t)(I(t)+R(t))-(μ+δ)R(t))dt+

σ3R(t)dB3(t)

(2)

式中：B,β,γ,δ,μ都是正数；S(0)>0,I(0)>0,R(0)>0,而Bi(0)=0。

SIRS谣言传播模型与目前广泛研究的传染病模型有着关键性区别，其中最本质的是谣言在传播者与社交圈中的其他人之间的传播是双向的。在传染病模型[20]中

dI(t)=βS(t)I(t)-(μ+γ)I(t)dt,
dR(t)=γI(t)-(μ+δ)R(t)dt

其中：β为传播率；μ为死亡率；γ为恢复率；δ为非免疫系数。谣言传播模型中dI(t), dR(t)多了非线性项γI(t)(I(t)+R(t))，这也使得后面模型的处理不能直接用常规的方法，很大程度上加大了讨论难度。

本文定义微分算子L，其与下列n维随机微分等式相关。

dx(t)=f(x(t),t)dt+g(x(t),t)dB(t),t≥t0

其中：随机过程x(t)∈Rn；f(t,x(t))是定义在[t0, +∞)×Rn上的n维函数；g(t,x(t)) 是一个n×m矩阵，f与g关于x满足局部李普希茨条件，令函数V∈C2, 1(Rn×R+;R)，则微分算子L作用于V函数有

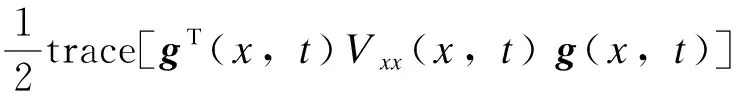
(3)

dV(x(t),t)=LV(x(t),t)dt+
Vx(x(t),t)g(x(t),t)dB(t)

(4)

2 全局正解的存在唯一性

(5)

τk=inf{t∈[0,τe)|S(t)∉(1/k,k)
或I(t)∉(1/k,k) 或R(τ)∉(1/k,k)}

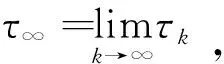
假设式(5)结论不成立，则存在T>0和ε∈(0,1)使得

P(τ∞ε

即存在整数k1≥k0，使得当k≥k1时

(6)

构造Lyapunov函数

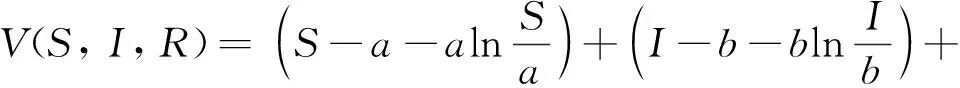
(7)

其中：a,b是一个正数。由于

因此式(7)为非负函数。

当t∈[0,T]和k>k1时,根据式(4)，两边求积分再取期望

(8)

其中

K+(aβ-μ)I+(bγ-μ)R

LV(S,I,R)≤K

(9)

K是一个大于零的常数。将式(9)代入式(8)两边求积分再去期望有

EV(S(t∧τk),I(t∧τk),R(t∧τk))≤V(S(0),
I(0),R(0))+EK(t∧τk)

(10)

EV(S(τk∧T),I(τk∧T),R(τk∧T))≤
V(S(0),I(0),R(0))+KT

(11)

又由式(10)和(11)得

V(S(0),I(0),R(0))+KT≥

E(ΙΩk(ω)V(S(τk,ω),I(τk,ω),R(τk,ω))≥

其中ΙΩk是Ωk上的示性函数。令k→∞，则有

∞>V(S(0),I(0),R(0))+KT=∞

因此可得τ∞=∞几乎必然成立，即S(t),I(t),R(t)不会在有限的时间内爆炸，则定理1得证。

3 随机谣言传播模型在边界平衡点附近解的渐近性质

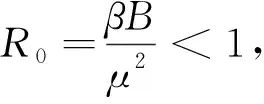
(12)

其中：

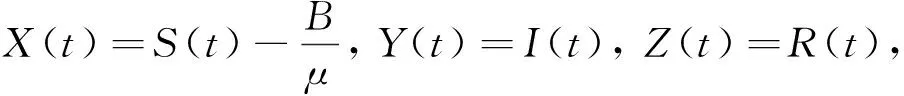
其中X∈R,Y>0,Z>0。考虑如下Lyapunov函数：

V(X,Y,Z)=(X+Y+Z)2+C1X2+C2(Y+Z)

其中C1,C2是一个正常数，会在后面给出。根据式(3)可得

-2μX2-2μY2-2μZ2-4μXY-4μXZ-4μYZ+2C1(-μX2-βX2Y-

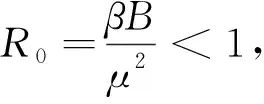
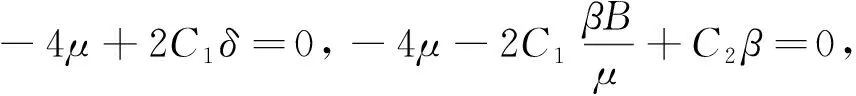
将上式代入式(4)，并对等式两边取积分后求期望有

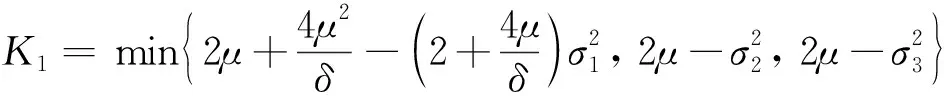
由此可得

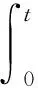
故有

即定理2得证。

4 随机谣言传播模型在正平衡点附近解的渐近性质

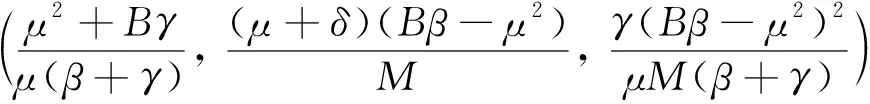
其中M=β(Bγ+μ2)+μδ(β+γ)。下面将讨论模型(2)在E*附近解的渐近性质。

(13)

证明：首先构造V(S,I,R)函数

V(S,I,R)=v1+C2v2+C3v3

(14)

其中：

v1=(S-S*+I-I*+R-R*)2+C1(S-S*)2

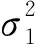
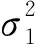
-2μ(S-S*)2-2μ(I-I*)2-2μ(R-R*)2-4μ(S-S*)(I-I*)+

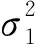
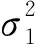
-2μ(S-S*)2-2μ(I-I*)2-2μ(R-R*)2-4μ(S-S*)(I-I*)+

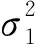
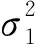
(15)

(16)

(17)

整理式(15)～(17)可得

LV(S,I,R)=Lv1+C2Lv2+C3Lv3≤

-2μ(S-S*)2+(-2μ-C2γ+C3γ)(I-I*)2-

2μ(R-R*)2+(-4μ+2C1δ)(S-S*)(R-R*)+

(-4μ+C2β-2C1βS*)(S-S*)(I-I*)+

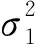
观察上式，令：

则有-4μ+2C1δ=0，-4μ+C2β-2C1βS*=0。那么式(18)可以转化为

LV(S,I,R)≤-2μ(S-S*)2-2μ(I-I*)2-2μ(R-R*)2-4μ(I-I*)(R-R*)+

-2μ(S-S*)2-2μ(I-I*)2-2μ(R-R*)2+4μI*R+4μIR*+

由不等式(a+b)2≤2a2+2b2可得

令

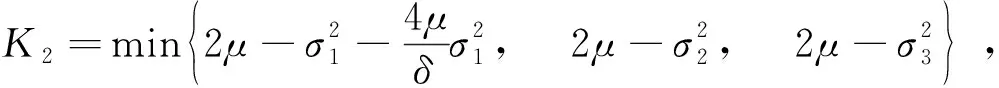
(18)

将式(18)代入式(4)，两边求积分并取期望有

0≤EV(S,I,R)=

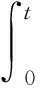
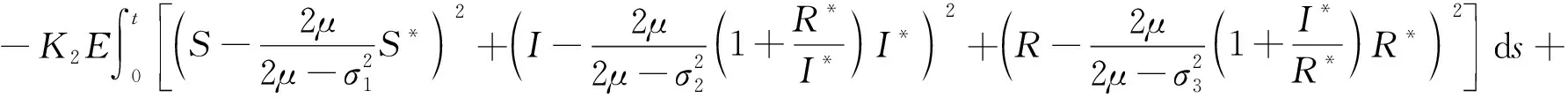
V(S(0),I(0),R(0))+M1t

则有

因此可得

即定理3得证。

5 数值模拟

根据模型(1)和模型(2)的实际意义取不同参数，用Matlab软件进行数值模拟[22-23]，通过模拟结果更直观地论证以上结论。这里用S1(t),I1(t),R1(t)表示模型(1)中人群，用S2(t),I2(t),R2(t)表示模型(2)中人群，并取步长为Δ=10-3。

例1:设定模型(1)和模型(2)初值S1(0)=S2(0)=0.8,I1(0)=I2(0)=0.4,R1(0)=R2(0)=0.2，各参数为B=0.4,μ=0.28,β=0.16,δ=0.1,γ=0.16,σ1=0.04,σ2=0.1,σ3=0.1。计算可得R0=0.8163<1，则根据定理2可知模型(2)的数值解在模型(1)边界平衡点附近徘徊，如图1所示

例2:设定模型(1)和模型(2)初值S1(0)=S2(0)=0.8,I1(0)=I2(0)=0.4,R1(0)=R2(0)=0.2。并设各个参数为B=0.8,μ=0.25,β=0.32,δ=0.2,γ=0.14,σ1=0.04,σ2=0.05,σ3=0.05。计算可得R0=4.096>1，则根据定理3可知模型(2)的数值解在模型(1)的正平衡点的附近徘徊，如图2所示

例3：在例2设置的各参数的基础上，改变随机因素干扰强度σi(i=1,2,3)的值，分别设置干扰强度(a)σ1=0.10,σ2=σ3=0.16; (b)σ1=0.05,σ2=σ3=0.008; (c)σ1=0.025,σ2=σ3=0.04;(d)σ1=0.0125,σ2=σ3=0.02。由图3可知，随机因素干扰强度对谣言传播的影响，干扰强度越大对谣言传播的干扰越大，干扰强度趋于0，则模型(2)的数值解曲线趋于平滑。

图1 边界平衡点附近解的渐近性Fig.1 Trajectories of the solutions around the disease-free equilibrium

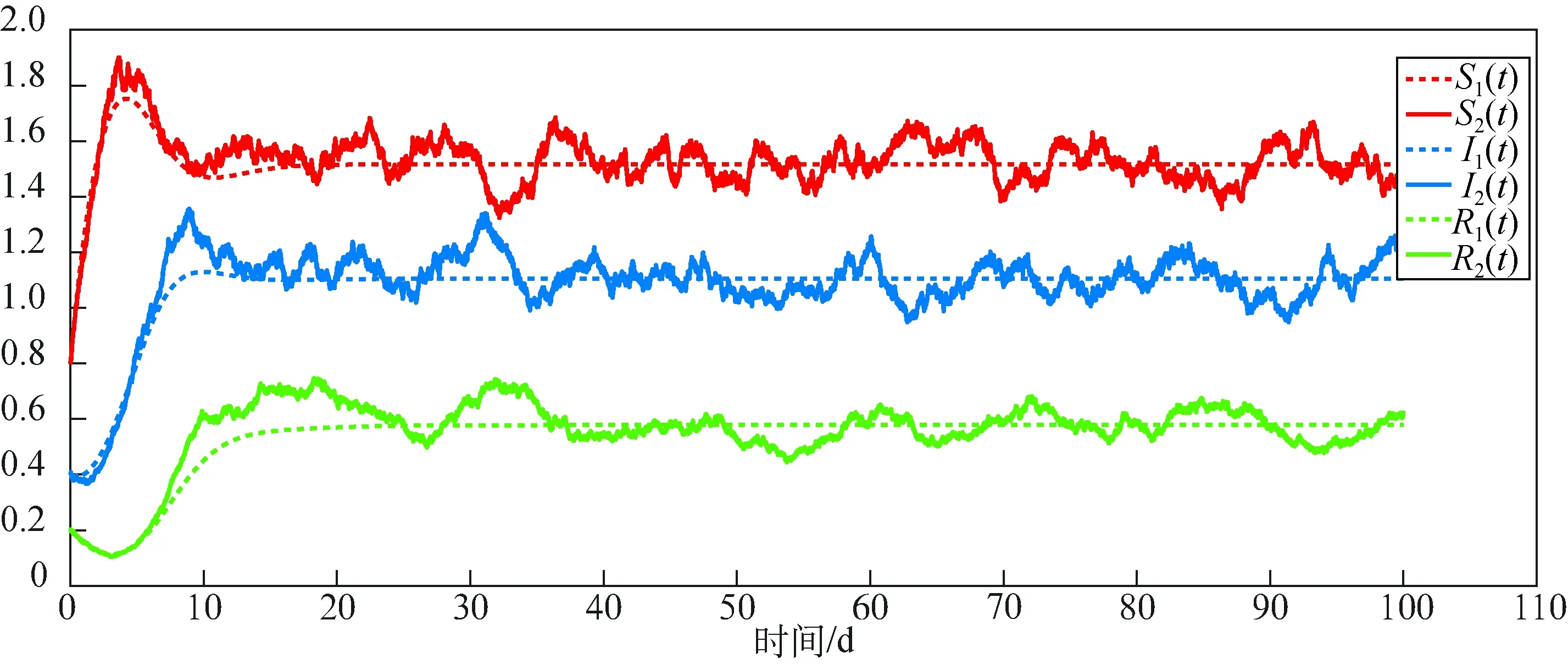
图2 正平衡点附近解的渐近性Fig.2 Trajectories of the solutions around the endemic equilibrium

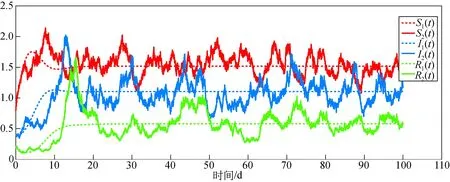
(a) σ1=0.10, σ2=σ3=0.16

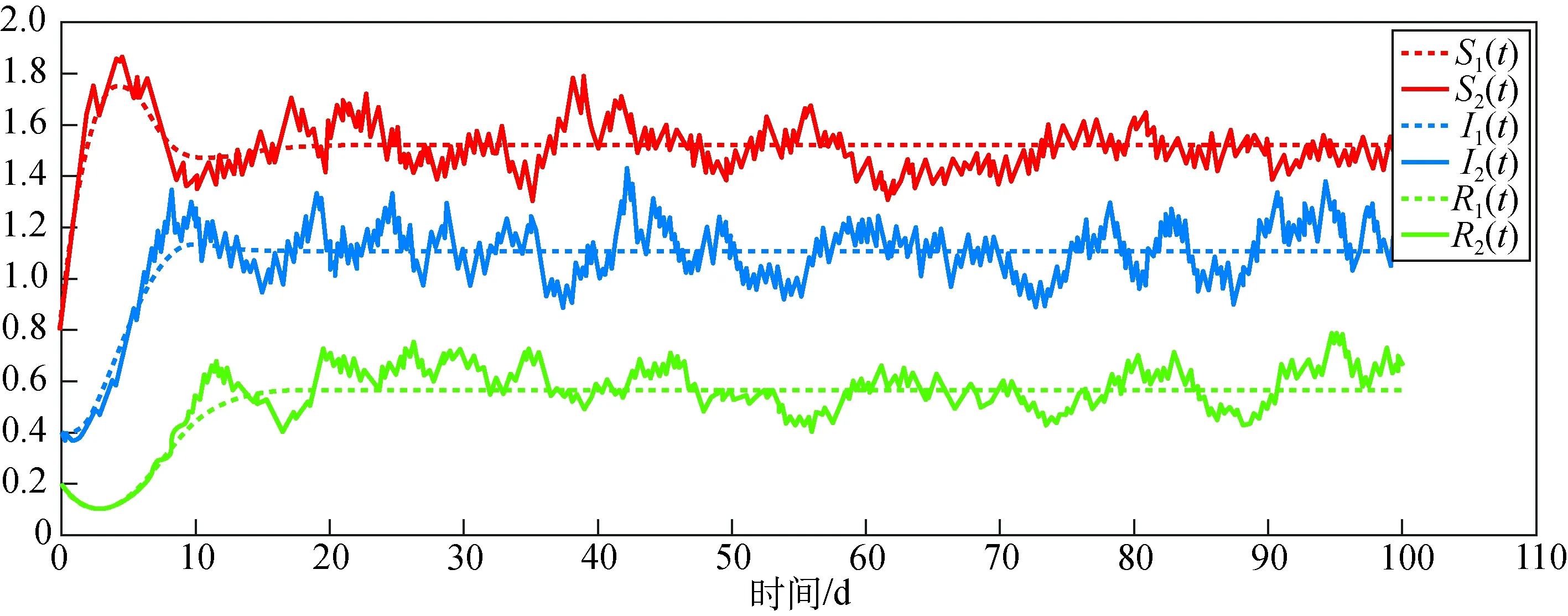
(b) σ1=0.05, σ2=σ3=0.008

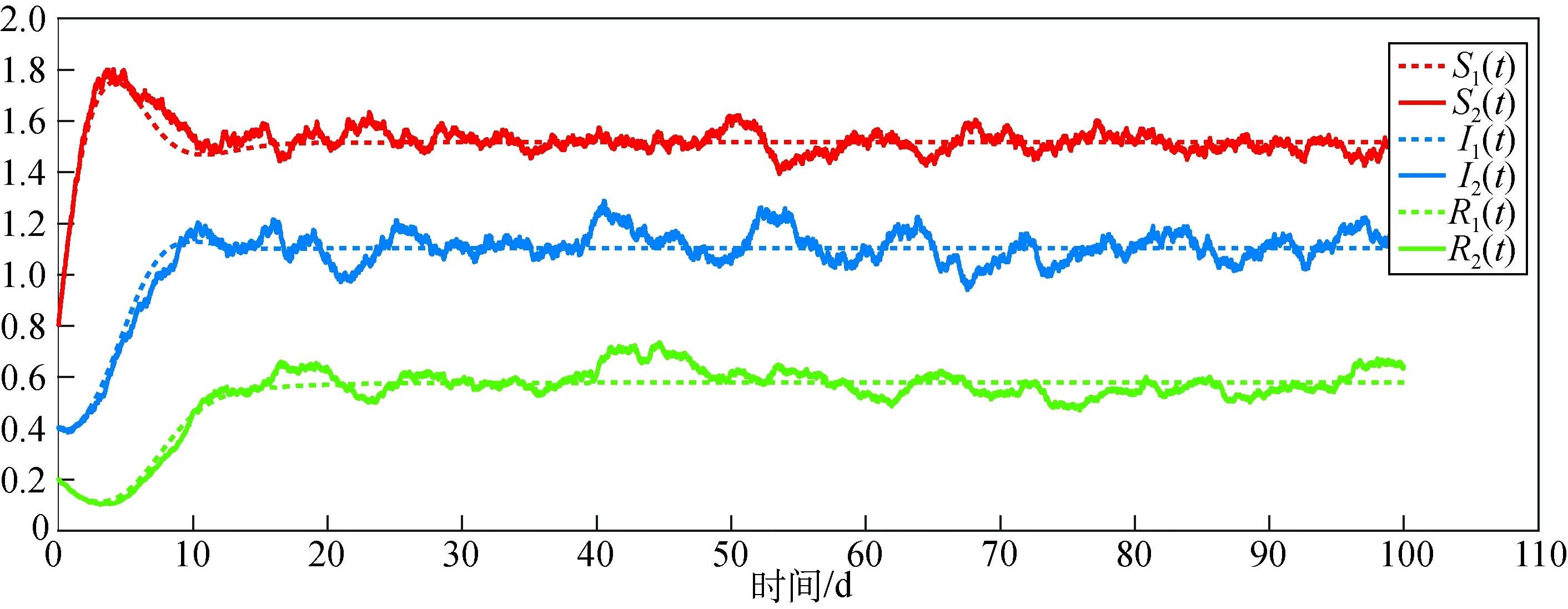
(c) σ1=0.025, σ2=σ3=0.04

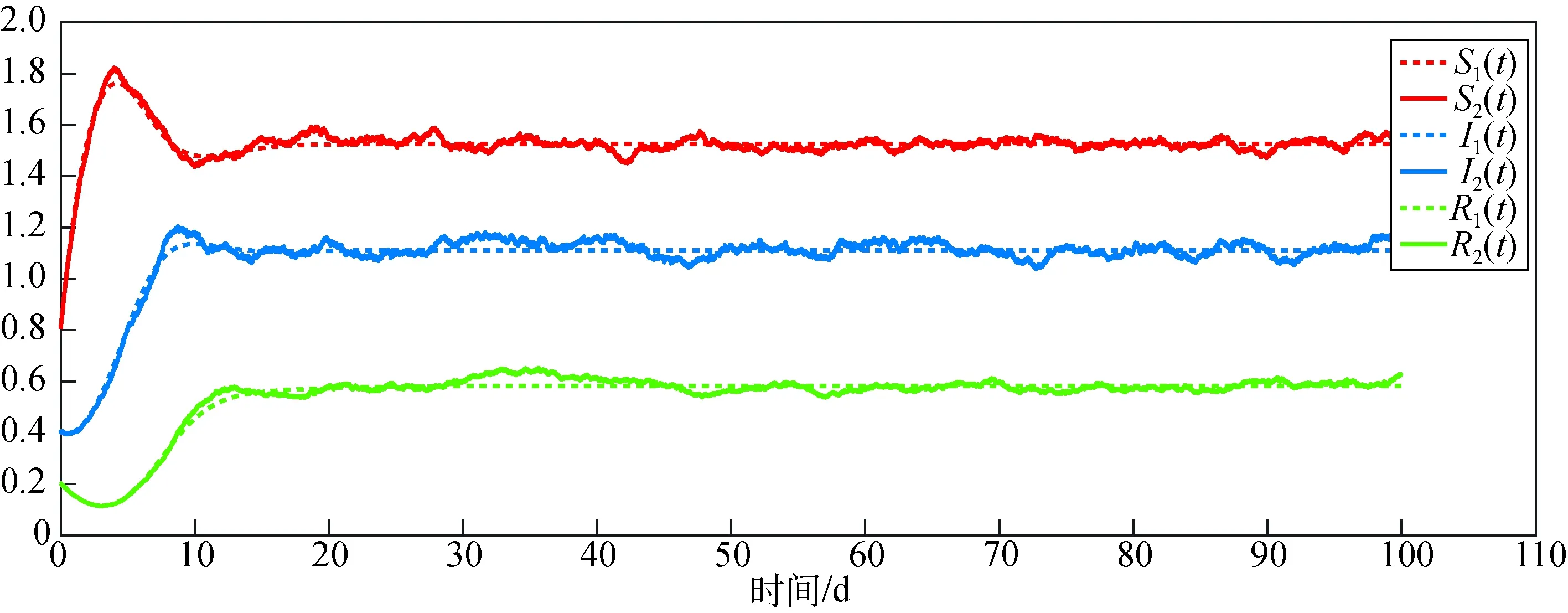
(d) σ1=0.0125, σ2=σ3=0.02

6 结 语

本文将人群分为3类，建立了SIRS随机谣言传播模型，并证明了其全局正解的存在唯一性。利用李雅普诺夫方法讨论了该模型在无谣言平衡点和谣言平衡点附近解的渐近性质，对谣言的传播做了更详细深入的研究。用Matlab进行数值模拟，将上述讨论用图像更清晰直观地表现出来。此外，研究中通过设置不同的随机因素干扰强度来表现随机因素对模型的影响。结合数值模拟可以清晰地观察到随机因素对谣言传播的影响，随机因素干扰强度越大则对谣言传播的干扰就越大，而干扰强度趋于0，对谣言传播的影响也趋于0。