一类具有非局部项的捕食食饵模型的动力学分析

张国颖， 彭亚红

(东华大学 理学院， 上海 201620)

捕食食饵模型在数学和生物学中扮演着非常重要的角色[1-2]。为了使该模型的适用范围更广泛，以及描述更加贴近现实，研究人员对捕食食饵模型进行了改进。例如在文献[3-4]中，研究者们用食饵种群的平方根描述捕食者与食饵之间的相互作用，得到了更加精确的模拟捕食者与食饵之间关系的模型如式(1)所示。

(1)

式中：X(t)和Y(t)分别表示t时刻的食饵与捕食者的密度；r和K分别表示食饵种群的增长率和环境容纳量；s表示没有食饵时捕食者的死亡率；α表示捕食者对食饵的搜索效率；c表示生物量之间的转化系数；th表示捕食者对食饵的平均处理时间。

Yuan等[5]把捕食食饵模型中捕食者的一次死亡率改为二次死亡率，对模型(1)进行如下无量纲变换:

并对其他参数作如下变换：

(2)

式中：d1和d2分别表示食饵和捕食者的扩散系数；uxx和vxx分别表示食饵和捕食者对x的二阶偏导。

当假设捕食者对食饵的平均处理时间为0(即a=0)时，模型(2)可简化为

(3)

Yuan等[5]利用线性化方法分析了模型(3)产生斑图的条件，并利用标准多尺度分析方法建立了振幅方程，以及通过数值模拟展示了模型(3)的点状斑图、条状斑图和点条混合斑图3种斑图形态。而Xu等[6]考虑到捕食者和食饵之间的生物转换量存在延迟现象，在模型(3)中引入时滞，选择时滞项作为分支参数，研究了相应模型常微分系统正平衡点的稳定性和霍普分支的存在性。Liu等[7]选择捕食者的一次死亡率，在齐次纽曼边界条件下，将prey-taxis引入捕食食饵模型，研究了相应模型在初边值条件下解的全局存在性，分析了正平衡点的存在性和稳定性，并利用抽象分支理论，以prey-taxis项作为分支参数，研究了非常数正解的稳定性以及稳态解的分支情况。

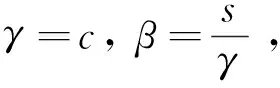
(4)

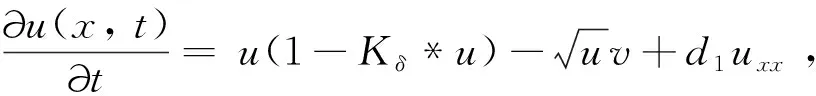
从生物角度而言，局部的反应扩散方程只能对位于一个空间点的个体与位于同一位置点的个体相互作用的情况进行建模，而非局部项描述两个物种的个体都可以从一个空间点移动到另一个空间点。核函数Kδ(x-y)表示消耗强度，测量位于空间点x的猎物与位于空间点y的猎物之间的竞争效率。由于不同个体的消费地点可以重叠，猎物之间开始争夺资源。核函数通常取标准概率密度函数。已有的研究中常用核函数包括以下3种：

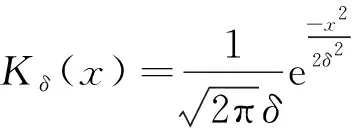
例如，文献[9]分别选取以上3种核函数，研究了具有非局部项的两类捕食食饵模型，讨论了非局部项对正平衡点的影响；Sherratt[10]也选取以上3种核函数，研究了具有非局部扩散项的微分方程的周期行波解。

若核函数分别取高斯函数和分段函数，那么得到下文模型(5)的特征方程都是超越方程，因此只能采用数值方法去分析模型的动力学行为。本文为了更加清楚地从数学理论上借助参数展现出非局部项的影响，选择拉普拉斯函数进行详细的分析与讨论。

(5)

本文主要研究无界区域(-∞, +∞)中非局部项对模型(5)正平衡点稳定性的影响，以及模型(5)产生图灵分支的条件，进而通过数值模拟例证了理论结果。

1 模型(5)正平衡点的稳定性分析

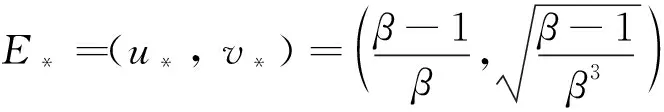
(6)

对模型(6)关于x作傅里叶变换为

(7)

模型(7)的特征方程为

λ2-Tkλ+Dk=0,k>0

其中

(8)

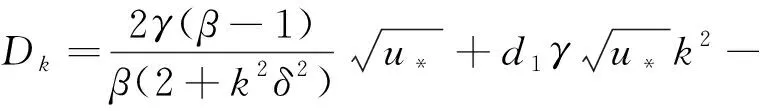
(9)

关于Tk和Dk给出如下两个引理。

引理1设d1，d2，δ和γ都是正数，β>1。

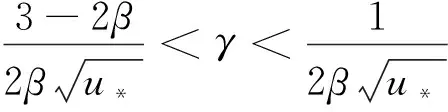
(10)

其中

(11)

(12)

(13)

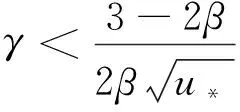
证明由式(8)可得

(14)

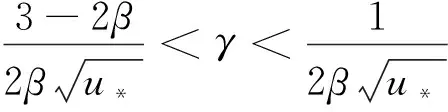
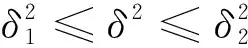
由于

且

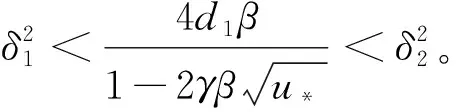
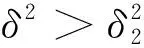
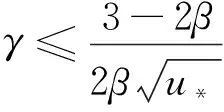
综上可知,引理1成立，证毕。

引理2设d1，d2，δ和γ都是正数，β>1。

(15)

其中

(16)

(17)

(18)

g(k2)=-2d1βδ2k4+(δ2-4d1β)k2+2(3-2β)

(19)

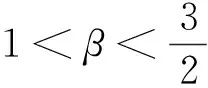
证明由式(9)可知

其中，g(k2)由式(19)给出。

其余的证明完全类似于引理1的证明，引理2结论成立。证毕。

结合引理1和引理2，得定理1。

定理1d1，d2，δ和γ都是正数，且β>1。

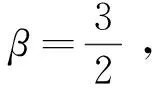
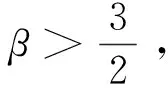
证明

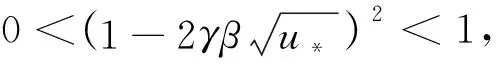
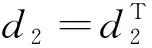
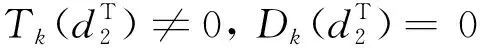
由引理1、引理2和条件H1，有定理2成立。

定理2d1,d2,γ和δ都是正数，β>1。

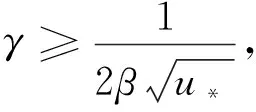
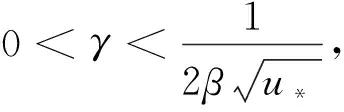
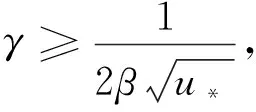
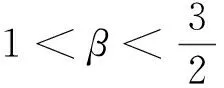
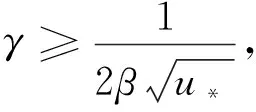
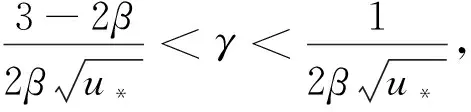
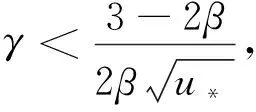
(20)

且

(21)

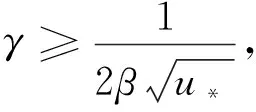
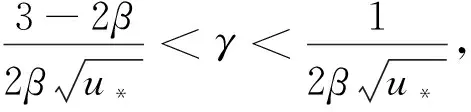
其中

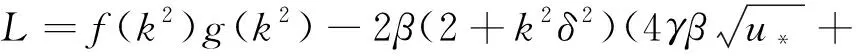
(22)

f(k2),g(k2)分别由式(13)和(19)给出，A(k2),B(k2),C(k2),D(k2)由式(21)给出。

由于

且

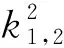
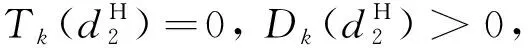
2 数值模拟

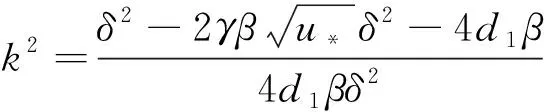
(a) δ=2.500

(b) δ=2.657

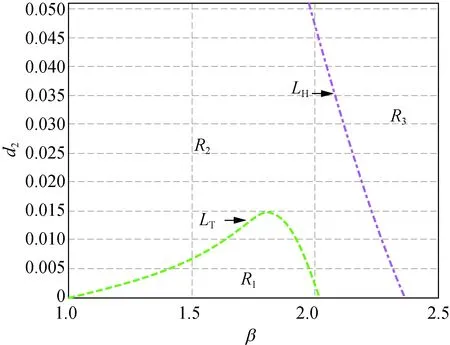
(c) δ=3.000

在图1中，曲线LH右(左)方有不等式Tmax<0(Tmax>0)成立；曲线LT的上(下)方有不等式Dmin<0(Dmin>0)成立。在图1(a)中，取δ=2.500时，曲线LH和LT相交于点A(1.933 , 0.037)，此时LH和LT所围成的阴影区域R2中，不等式Tmax<0和Dmin>0同时成立，即R2为模型(5)正平衡点的稳定性区域。随着δ增大，当取δ=2.657时，在图1(b)中，曲线LH和LT相切于点B(2.16 0, 0.007)。δ继续增大，当取δ=3.000时就得到图1(c)，此时曲线LH和LT相分离。所以图1中随着δ从2.500增加到2.657直到3.000，阴影区域逐渐变小，直到消失，也即随着δ的变化，模型(5)正平衡点的稳定性被破坏。

但是，当δ从3.000继续增大到3.300时，曲线LH与LT会重新出现交点，也即正平衡点的稳定区域会随着δ的增大重新出现。接下来分别取δ=3.300，4.000，5.000和6.000时得到图2。

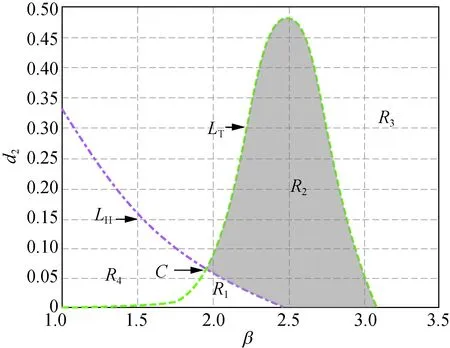
(a) δ=3.300

(b) δ=4.000

(c) δ=5.000

(d) δ=6.000

在图2中，曲线LH和LT分别相交于点C(1.948, 0.064)，D(2.314, 0.033)，E(2.429, 0.036)和F(2.610, 0.031)，阴影区域R2为稳定性区域。由此可知，随着δ的增加，阴影区域的面积会发生变化，并且阴影区域将沿着β轴后移。图2与图1相比较可知，当δ>3.300时，模型(5)正平衡点稳定区域将一直存在。

此外，在图1和图2中，区域R1中Tmax>0且Dmin>0成立，此时存在k>0使得Tk>0，称R1为霍普区域；区域R3中Tmax<0且Dmin<0成立，此时存在k>0使得Dk<0，称R3为图灵区域。图1(a)和图2(a)～(d)中的区域R4，以及图1(b)～(c)中区域的R2都有Tmax>0及Dmin<0成立，故称图1(a)和图2(a)～(d)中的区域R4，以及图1(b)～(c)中区域的R2为图灵霍普区域。

3 结 语

本文将非局部项引入具有二次死亡率的捕食食饵模型，选择拉普拉斯核函数作为空间卷积项，研究了非局部项对模型(5)正平衡点稳定性的影响。研究表明，随着非局部项中参数δ的变化，正平衡点的稳定性区域也发生变化。数值模拟例证了理论结果，并且展示出了非局部项的存在甚至可以使模型(5)正平衡点的稳定性区域完全消失的现象。