多响应线性混合效应模型的A- 最优设计

段冬艳， 刘 欣

(东华大学 理学院， 上海 201620)

混合效应模型作为分析纵向数据、重复测量数据和面板数据等的常用工具，在诸多领域得到了应用。从畜牧养殖到群体药代动力学、从空间统计到个体化医学都可以找到成功应用的案例[1-3]。随着计算机技术的发展，对混合效应模型的统计分析和应用都取得了长足的进展。由文献[4-6]可知，目前混合效应模型的性质已经得到了很好研究。

在许多实际问题中，响应向量往往同时具有多个组成部分，并且这些组成部分可能相互关联，研究者须对这些部分进行联合建模，多响应混合效应模型是分析这类数据的重要工具。例如：Dahm等[7]采用多响应混合效应模型分析动物育种试验；Sun等[8]利用两响应混合效应模型研究1973—1977年在乌普萨拉市出生的独生子女的生长曲线；Verbeke等[6]采用多响应线性混合效应模型分析收缩压和舒张压的试验数据；Jensen等[9]采用多响应线性混合效应模型分析空气质量与办公室工作绩效之间关系的试验数据。

混合效应模型的分析结果与获取数据的试验方案有着密切的联系，如试验中变量的观测时间和药物的剂量等试验条件的设置都会直接影响最终统计推断的效力。如何有效安排试验是试验设计的目的。最优试验设计方法作为试验设计理论的一个重要分支，正被越来越多地应用于混合效应模型的试验设计研究中。在单响应混合效应模型的最优设计方面：Entholzner等[10]研究得出在混合模型下的最优和最有效的设计；Schmelter[11-12]考虑了随机系数模型中单群恒等设计的最优性和多群恒等设计的最优性问题；文献[13-15]分别对随机截距模型、随机斜率模型和三次回归随机系数模型的优化设计进行了研究；文献[16-17]讨论了具有随机截距项的线性和二次回归模型的V- 最优设计和D- 最优设计；文献[18]研究了分层模型中个体参数的最优设计。

本文研究多响应线性混合效应模型的A- 最优设计。A- 最优设计准则是最常用的设计准则之一，其统计意义在于使未知参数估计量的各分量方差之和最小，因此A- 最优设计能最大程度地提高参数估计的精度[19]。

1 模型和估计

假设试验共有n个被试个体，对第i个个体进行mi次观测。将第i个个体的第j次试验点xij处的观测记为yij，其具有r个分量，可根据式(1)计算得出。

yij=F(xij)βi+εij,i=1, …,n,j=1, …,mi

(1)

式中：试验点xij∈χ，χ为设计区域；F为r×p维回归函数矩阵；εij为均值为0、协方差矩阵为Σ的观测误差向量；βi为个体参数。βi的均值E(βi)=β；协方差矩阵Cov(βi)=D，D为半正定矩阵，其秩为q。假设随机效应与观测误差相互独立，不同次试验的观测误差之间相互独立。

通过分离固定效应和随机效应，可将模型(1)改写为

yij=F(xij)βi+F(xij)bi+εij,
i=1, …,n,j=1, …,mi

(2)

式中：bi=βi-β是个体参数与总体均值的差值。在模型(1)和(2)中，响应向量yij的协方差矩阵为Cov(yij)=F(xij)DFT(xij)+Σ。同一个体的不同观测之间是相关的，其协方差阵为Cov(yij,yik)=F(xij)DFT(xik),j≠k。不同个体之间的观测是相互独立的。将第i个个体的所有观测记为Yi=(yTi1,yTi2, …,yTimi)T，其矩阵形式为

Yi=Fiβ+Fibi+εi

Y=Xβ+Zb+ε

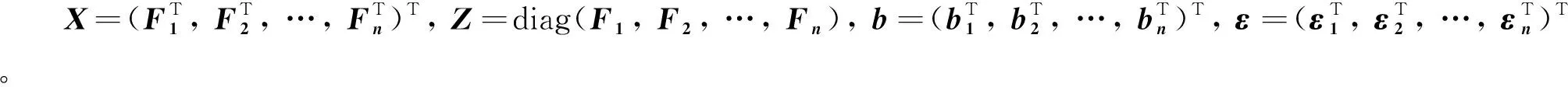
式中：N=m1+m2+…+mn为总观测次数。

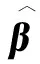
式中：R=Cov(ε)=ΙN⊗Σ；G=Cov(b)=Ιn⊗D。

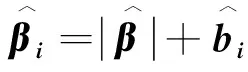
2 最优设计

为准确预测个体参数βi，本文期望通过试验设计使MSE矩阵在某种程度上达到最小。在考虑平衡设计的基础上，假设试验设计有k个不同的试验点x1,x2, …,xk，重复数分别为n1,n2, …,nk，可将其记为

进一步考虑Kiefer[22]定义的近似设计，即只要求

对任一近似设计ξ，其标准化信息矩阵定义为

式中：Δ=mD。当D非奇异时，可将MSE矩阵简化为

由于预测的精度可以通过MSE矩阵来刻画，此处借鉴A- 最优设计的思想，定义准则函数为

(n-1)tr{Δ-Δ(M-1(ξ)+Δ)-1Δ})

令Ξ表示在χ上具有非奇异信息矩阵的所有近似设计的集合。

定义1如果设计ξ*，使得

成立，则称ξ*为个体参数的A-最优设计。

下面的等价性定理给出了设计为A-最优的充要条件。

定理1记N(ξ,Δ)=Δ(M-1(ξ)+Δ)-1。令

φ(x,ξ)=tr{M-1(ξ)FT(x)Σ-1F(x)M-1(ξ)}+

(n-1)tr{N(ξ,Δ)M-1(ξ)FT(x)Σ-1F(x)M-1(ξ)NT(ξ,Δ)}

当且仅当

则设计ξ*是个体参数的A-最优设计，并且在设计点ξ*处达到上确界。

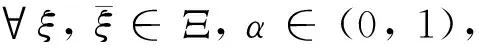
以及

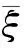
(n-1)tr{Δ(M-1(ξ)+Δ)-1M-1(ξ)(M(ξ)-

(n-1)tr{N(ξ,Δ)M-1(ξ)NT(ξ,Δ)}-

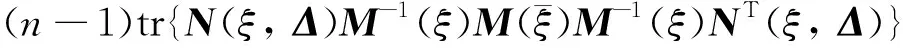
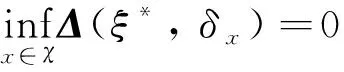
推论1当D非奇异时，令

φ(x,ξ)=tr{M-1(ξ)FT(x)Σ-1F(x)M-1(ξ)}+

(n-1)tr{(M(ξ)+Δ-1)-1(FT(x)Σ-1F(x)+
Δ-1)(M(ξ)+Δ-1)-1}

(3)

当且仅当

则设计ξ*是个体参数的A-最优设计，并且在设计点ξ*处达到上确界。

例1带有随机截距的线性回归模型求解A-最优设计

Kubokawa等[24]利用线性混合效应模型分析神奈川县各地至附近车站的距离和附近车站到东京车站距离对该区域地价影响。神奈川县的许多居民常乘火车往返东京，所以居住地到附近车站和附近车站到东京车站的距离会影响地价，Kubokawa等[24]运用如式(4)所示的模型对1996和2001年的地价数据进行分析。

y1ij=β10+β11x1ij+β12x2ij+b1i+ε1ij

y2ij=β20+β21x1ij+β22x2ij+b2i+ε2ij

(4)

式中：y1ij和y2ij分别代表1996和2001年第i个小区域、第j个地块的地价，i=1, …,n,j=1, …,m, (x1ij,x2ij)∈[-1, 1]2；x1ij表示该地块到附近重要车站的(标准化)距离，x2ij表示该地块附近车站到东京站的(标准化)距离。随机效应bi=(b1i,b2i)T的协方差阵为Σb，误差向量εij=(ε1ij,ε2ij)T的协方差阵为Σ，并且bi和εij相互独立。本例考虑模型(4)的最优设计问题，利用定理1证明设计

是随机效应的A-最优设计。

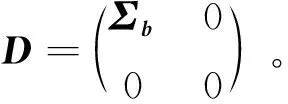
记H≡(Σ+mΣb)-1，由计算可得

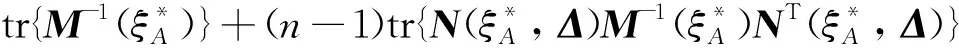
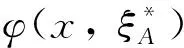
注：例1给出的A- 最优设计既与随机效应的方差协方差矩阵无关，也与误差的方差协方差矩阵无关，这一点对其他模型不一定成立。