考虑两阶段销售的线上时尚服装零售商优化定价和服务决策
徐 琪, 赵 婉
(东华大学 旭日工商管理学院,上海 200051)
近年来随着经济的快速稳健发展,电子商务以其独特的优势广泛渗透到社会生活各个领域,成为经济增长和社会发展的新动力。《2017年中国电子商务市场数据监测报告》显示,2017上半年中国电子商务交易额为13.35万亿元,同比增长27.1%。其中,多年来时尚服装类产品在网上购物品类中名列第一,而服装类产品又属于典型的时尚性、季节性产品,产品体验对消费者的购买行为影响很大。为此,许多互联网企业纷纷利用先进的信息技术、大数据技术加强购物体验服务,以应对网络零售运营的新变化。例如,阿里巴巴推出 “淘宝Buy”,H&M携手Google试行Data Dress,eBay收购3D虚拟试衣公司Phisix。由此可见,线上服装零售商考虑服装的时尚属性,并据此制定相应的体验服务水平和售价,对服装企业提升效益以及获得更大的竞争优势具有重要的意义。
然而,网络消费者的体验服务如何吸引更多顾客通过电商渠道完成交易,如何维持顾客忠诚度,增加零售商的市场份额和利润,是网络服装零售企业面临的现实问题,在学术上亦有较大的探讨空间。由于时尚服装属于短生命周期产品,其定价策略和服务决策与易逝品有相同之处,消费者多为策略型消费者[1-6],故本文从易逝品动态定价、服装的时尚属性、体验服务进行文献梳理。
现阶段易逝品的动态定价策略研究忽视了服装行业的时尚属性。时尚服装与普通易逝品有所区别,前者的时尚元素是其不容忽视的重要属性。周建亨等[7]针对服装市场需求短期骤减、长期缓慢下降的特点分析了供应链成员的订货策略;吴胜等[8-9]研究了新产品处于不同销售周期阶段下零售商的定价问题。虽然二者一致认为,时尚服装的价值由功能价值和时尚价值两部分构成,但是都没有针对时尚属性进行深入探讨或建模。Chen等[10]认为,时尚度是时尚服装质量的外在表征,并引入时尚程度(简称时尚度因子)加以描述,研究表明时尚度因子随着时间的流逝而降低。陈啟等[11]在文献[10]基础上考虑了体验服务因素并对时尚度因子进行了模型改进,研究表明,时尚度不仅受时间因素的约束,还与零售商的体验服务投入有关,投入越大则时尚度衰减的速度越慢。然而,时尚产品的动态定价策略研究中鲜少提及策略型消费者。基于此,本文针对服装行业的时尚属性,考虑了市场中仅存在策略型消费者情形的服装产品的动态定价策略。
从已有文献来看,体验服务的研究主要集中于体验服务对供应链协调机制和零售商运营策略影响的探讨。近年来,体验服务对供应链运作的影响逐渐吸引了学术界的关注。但斌等[12]的研究表明两部收费策略可以实现双渠道供应链的完美协调。当顾客在消费过程中的耐心程度较低时,零售商可以考虑引进线上下单服务。Gao等[13]通过构建理论模型研究发现,当客户等待敏感性较高时,企业采取线上自助点餐技术可以提高收益。但是,双渠道供应链环境下的服务决策更关注于单一渠道提供服务的情形,忽略了O2O(online to offline)的现实背景。随着线上线下的快速融合,全渠道销售成为趋势,学者开始聚焦于体验服务对全渠道供应链运作的影响研究,重点围绕O2O和BOPS(buy online and pick up in store)两种商业模式。O2O模式多为线上、线下均提供体验服务,如范丹丹等[14]在文献[15-17]的基础上,设计了需求迁移情景下的集中式和分散式模型,得到O2O系统最优条件下的服务决策。BOPS模式主要为线下提供体验服务,如严建援等[18]的研究表明,不管线上、线下价格同步与否,以及是否提供服务的情形下,制造商的批发价都不发生改变。时尚行业背景下的运营问题多从供应链视角出发,而立足于零售商进行研究的文献是屈指可数的。文献[11]在考虑体验服务影响服装时尚程度的基础上,对比分析了是否采取打折促销策略对于零售商价格和订购量决策的影响,结果表明,若零售商进行打折促销,选取恰当的时机有利于清理库存和提高收益。但是,以上体验服务决策研究缺少对策略型消费者的思考,此外体验服务的提供方多为线下,几乎没有线上提供体验服务的探索。
基于上述研究,本文首先考虑策略型消费者情形,研究动态定价问题。其次,将服装价值归纳为时尚价值和功能价值两方面,不同销售周期消费者支付意愿的时间偏好有所差异,随着时间的推移,消费者对服装时尚价值的感知降低较快,对功能价值的感知亦在减弱。然而,相关文献并没有针对时尚产品的特点对时尚服装的价值加以区分。本文根据时尚服装在产品生命周期不同阶段呈现的特点对效用函数进行研究,通过效用函数模型进一步构造需求函数,更加符合现实情境。
1 问题描述
考虑一个时尚服装线上零售商提供体验服务,客户可以通过淘宝等网购平台浏览快时尚品牌商发布的时尚产品,并在线上下单,经过物流配送收到产品最终完成交易。该情形下,考虑策略型消费者并参照文献[7-9]的研究,将时尚服装销售周期划分为新品上市期和打折促销期,产品价值包括时尚价值和功能价值两方面,且价值能够被消费者直接观测到,从而影响消费者的行为活动,并进一步作用于市场需求。对此,本文将探讨线上服装零售商如何针对不同销售时期制定两阶段动态定价和服务决策。在新品刚上市期间,服装设计理念最为新潮,时尚元素备受瞩目,消费者对其估值包括时尚和功能价值两方面,此外,通过3D虚拟试衣等体验服务可以提高消费者关于服装时尚价值的估值。消费者对于时尚服装的估值过程如图1所示。

图1 一个销售周期内消费者对时尚服装的感知价值Fig.1 Consumer perceived value of fashion apparel during a sales cycle
新品投放市场一定时期后,服装的时尚价值迅速降低,线上零售商不得不进行货品价格调整,为下一个阶段做准备;经过短暂的过渡期,服装进入打折促销阶段,服装的功能价值在消费者感知价值中将占主导地位(如羽绒服的功能价值体现在保暖御寒等作用),并且打折期间若存在物流延迟等现象,将导致服装的功能价值出现一定程度的下降。考虑到现实中打折价对于消费者而言已经具备了足够吸引力,因此,此阶段线上零售商不提供额外服务。
2 模型建立
2.1 消费者效用函数
由图1可知,时尚服装的销售周期大致分为新品上市期、过渡期和打折促销期。考虑到过渡期时间短且变化复杂等特点,本文结合快时尚服装的生命周期特征,从线上零售商的视角,分析新品上市期和打折促销期两个阶段的消费者效用和购买行为。
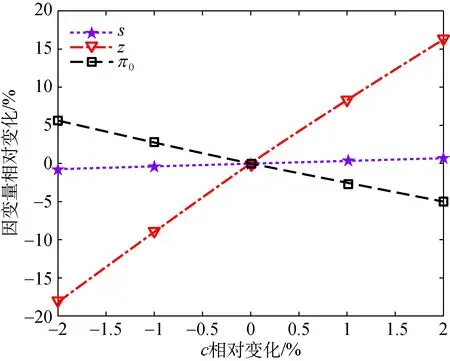
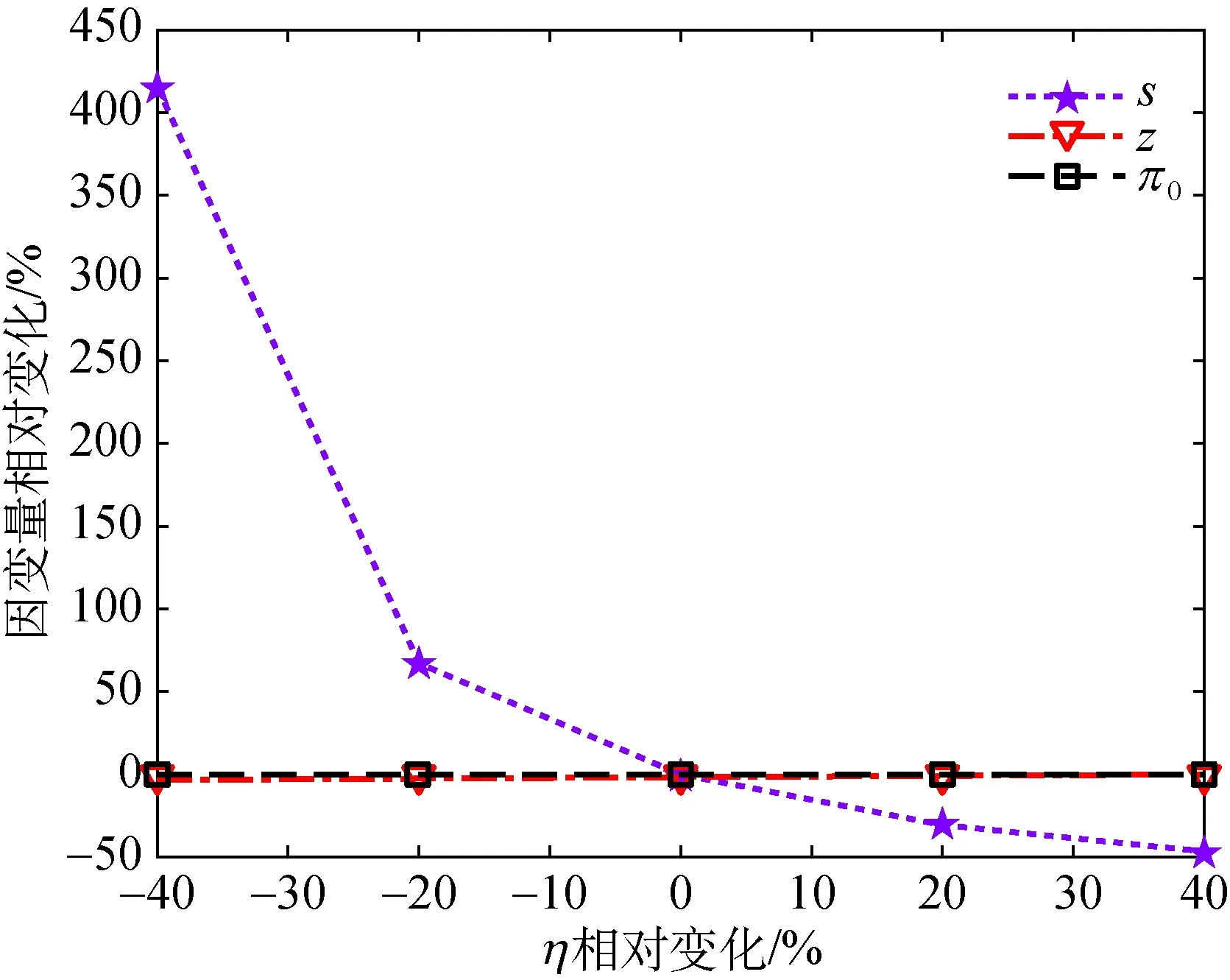
在新品上市期,服装处于时尚状态,线上零售商制定价格p1,消费者感知价值来源于功能价值和时尚价值两方面。假设消费者对服装的功能价值估值为μ,对服装的时尚价值估值为v,且二者取值范围为(0,1];α、β分别代表消费者对服装功能价值、时尚价值的敏感系数(0≤α≤1且0≤β≤1),由此得到消费者的初始效用为αμ+βv-p1。该阶段线上零售商通过提供“3D虚拟试衣”等体验服务提升消费者对服装时尚价值的认知,服务水平为s,提供服务后该服装的时尚价值增加了ks倍,于是,消费者在新品上市期购买服装获得的最终效用为U1=αμ+βv(1+ks)-p1,其中k表示s对β的影响程度。打折促销期,服装降价处理,线上零售商以价格p2(p2 图2 两阶段消费者效用与购买决策Fig.2 Two-stage consumer utility and purchasing decisions 由图2可知,当U1=0,U2=0和U1=U2时消费者的购买意愿分别与无差异曲线A、B、C相对应。根据策略型消费者的特点,线上零售商会比较消费者在第一、二阶段购买该服装的效用及其零之间的大小关系,以此进行购买决策。结合图2可知,消费者是否购买以及何时购买取决于效用的大小。当U1>U2>0时,消费者选择在新品上市期购买;当U2>U1>0时,消费者选择在打折促销期购买;U1<0或U2<0的条件下,消费者不会购买。 现有文献通常将消费者分为策略型和短视型两类。策略型消费者往往具有丰富的购物经验,他们会观察同类产品的历史价格进而形成未来销售阶段对目标产品的价格预期,尽一切可能以最低价格购买产品,通常选择等待产品促销或清仓时期购买;相对应地,短视型消费者处于目标产品销售周期任一阶段都会放弃等待立即购买。参照文献[1]的研究,本文中目标市场的客户群均为策略型消费者,这类消费者会比较时尚服装在新品上市期、打折促销期的效用和零效用,从而做出是否购买的决策,若选择购买,会在最合适的时机进行消费。相应地,顾客策略行为通过效用函数体现并影响需求。 证明:需求函数按服装销售周期可以分为两个阶段,即第一阶段为新品上市期和第二阶段为打折促销期,分别用下标“1”“2”来表示,并且取决于策略型消费者的效用函数。 当U1=0时,消费者是否在新品上市期购买则取决于μ1=[p1-βv(1+ks)]/α;当U2=0时,消费者是否在打折促销期购买则取决于μ2=p2/(θα);当U1=U2时,消费者在新品上市期购买还是等待打折再买则取决于阈值μ0=[p1-p2-βv(1+ks)]/[α(1-θ)]。 由于已知参数范围无法比较μ2和μ1的大小,因此分两种情况讨论,进一步判断消费者的购买决策。 已知0<α≤1,0<θ<1,进而推导可知μ1>μ0,因此μ0<μ1<μ2。 首先构建新品上市期的需求函数。对于策略型消费者而言,其会比较在新品上市期、打折促销期购买该服装的效用,当U1大于U2且U1>0,即μ>max(μ1,μ0)时,策略型消费者不愿等待,服装新品一经发布就会进行购买。已知μ0<μ1,则满足μ>μ1的条件下消费者会选择在新品上市期购买,此时新品上市期的需求为q1=1-μ1=1-[p1-βv(1+ks)]/α。 然后构建打折促销期的需求函数。打折促销期,服装销售价格降为p2,只有该阶段的效用为正且U2大于U1的条件下,策略型消费者才会选择在打折促销期购买,即μ1<μ<μ0时,策略型消费者会选择等待至打折促销期时购入该服装。μ1<μ2的情况下,μ0<μ2,与μ2<μ<μ0相悖,因此打折促销期的需求为q2=0。 由μ1≥μ2可得μ1>μ0,综上μ0>μ1≥μ2。 现实中新品上市期和打折促销期均有顾客光临(即都有需求产生),因此两阶段对应的需求(订购量)分别为 (1) (2) 线上零售商在某服装销售周期内的总利润由新品上市期和打折促销期的利润构成。由2.1节可知:新品上市期线上零售商的收入来源于该阶段的服装销售,支出用于负担服装订购和体验服务方面的成本;对于打折促销期,由于打折已经具备相当大的吸引力,且考虑到现实生活中线上零售商一般不提供额外的服务,因此线上零售商该期间的支出仅用于服装采购,收入同样来源于该阶段的服装销售。据此分别构建时尚服装线上零售商新品上市期、打折促销期的利润函数分别如式(3)和(4)所示,总利润函数如式(5)所示。 线上零售商在新品上市期的期望利润为π1=(p1-c)q1-ηs2/2,将式(1)代入该式,可得 (3) 式中:c为单位订购成本;η为体验服务成本系数。 线上零售商在打折促销期的期望利润为π2=(p2-c)q2,将式(2)代入该式,可得 (4) 由于时尚服装的新品上市期和打折促销期的间隔时间极短,因此不考虑打折促销期利润的贴现,线上零售商在某服装一个销售周期内的总利润为 (5) 运用逆向求解法求解时尚服装线上零售商在新品上市期和打折促销期两阶段的价格和服务。 在打折促销期,已知新品上市期间线上零售商提供的体验服务水平及制定的服装售价,在此基础上线上零售商制定打折促销期的服装价格策略。根据前面讨论,打折促销期的最优解问题可描述为 (6) 对于式(6)的线性规划问题,使用库克塔克条件,首先构造Lagrange函数并将约束转化为一阶KKT(Karush-Kuhn-Tucker)条件,如式(7)所示。 maxL2(p2,λ1,λ2)= (7) 在新品上市期,已知线上时尚服装零售商在打折促销期的定价,顾客基于价格预期采取行动。线上零售商据此进行本阶段的服装售价和体验服务水平决策。 M1=4k2β2v2-4θk2β2v2+θ2k2β2v2 M2=8αη-14αηθ+6αηθ2 M3=4αkβv+cθkβv-8αθkβv-cθ2kβv+4αθ2kβv M4=4cηα+4ηα2-6cηαθ-8ηα2θ+2cηαθ2+4ηα2θ2+4αβηv-8αβηθv+4αβηθ2v M5=2αθ2k2β2v2-2αθk2β2v2-cθ2k2β2v2+2cθk2β2v2-2ck2β2v2 (8) 其中: A0=θβ2v2+2θkβ2v2s+s2[2αηθ-2αη+θk2β2v2] A1=(3θ-4)p12-4p1(θ-1)(α+βv+ksβv) (9) 将式(8)代入海森矩阵判定公式中,化简计算得到的结果如式(10)所示。 (10) 同理,构造Lagrange函数和KKT条件为 maxL0(p1,s,λ1,λ2,λ3)=(p2-c)A2+λ1A3+ λ2(p2-p1)+λ3(c-p2) (11) 其中: A4=2α-2αλ2+αθλ2-αθλ3-λ1+2βv+2skβv A5=2s[2αη(θ-1)+θk2β2v2]+2kβv[λ1-θλ1+ αθ(θ-1)(λ2-λ3)+θβv] 针对某服装单一销售周期的优化策略进行模型分析。给定消费者关于服装的时尚价值估值v,根据命题1中各参数的约束对体验服务成本系数η、打折促销期的评估折扣θ、功能价值敏感系数α、服务水平s对时尚价值敏感系数β的影响程度k赋值,观察时尚价值敏感系数β如何影响最优解和两阶段的需求。 命题2:给定体验服务成本系数η、打折促销期的评估折扣θ、功能价值敏感系数α,以及服务水平s对时尚价值敏感系数β的影响程度k等参数,服务水平s随着时尚价值敏感系数β的增大而减小。 证明:s*对β求导得到式(12)。 (12) 其中: 以上表达式较为复杂,无法直观判断正负,根据已知参数取值范围和命题1的约束,计算得到∂s*/∂β>0。该结论符合现实,消费者对于服装时尚价值的敏感系数β越大,说明相对于服装的功能价值,消费者更看重其时尚价值。面对这类消费者,线上时尚服装零售商应该提升体验服务水平,从而使服装的时尚价值随体验服务水平的提高而上升。 命题3:给定体验服务成本系数η、打折促销期的评估折扣θ、功能价值敏感系数α,以及服务水平s对时尚价值敏感系数β的影响程度k等参数,时尚服装新品上市期的单位服装售价p1随着时尚价值敏感系数β的增大而上涨,打折促销期的单位服装售价p2随着时尚价值敏感系数β的增大而下降。 (13) (14) 其中: M9=k2βv[βv(2-θ)2+2c(1-θ)θ]+ 命题4:给定体验服务成本系数η、打折促销期的评估折扣θ、功能价值敏感系数α,以及服务水平s对时尚价值敏感系数β的影响程度k等参数,时尚服装新品上市期的市场需求q1随时尚价值敏感系数β的增大而增大, 打折促销期的市场需求q2随时尚价值敏感系数β的增大而减小。 证明:q1和q2分别对β求导得到式(15)和(16)。 (15) (16) 其中: M10=[βv(2-θ)2+2c(1-θ)θ]+ 同理,观察式(15)和(16),根据已知参数范围可以直接判断∂q1/∂β>0,∂q2/∂β>0。实际生活中,消费者在购买服装时越关注服装的时尚价值,则β越大,消费者越倾向于选择在新品上市期间购入,因此,第一阶段需求增加。 根据命题1中的条件进行参数设置:k=0.6,η=2,θ=0.5,α=0.5,c=0.05,β=[0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9],观察β如何影响线上零售商各项运营指标的变化,即时尚价值敏感系数β对服务水平s、服装促销期的价格折扣p2/p1(用z表示,即z=p2/p1)、需求qi(i=1,2)和利润πi(i=0,1,2)的影响,通过分析计算得到结果如表1所示。 表1 服装时尚价值敏感系数β对线上零售商运营指标的影响 观察表1可知:消费者对服装的时尚价值敏感系数β增大,意味着在消费者感知价值中时尚价值越来越重要,只要提高新品上市期的服务水平s,就能进一步增加强消费者对服装时尚价值的认可;线上零售商在逐渐提高新品上市期的服装售价p1的同时,为了吸引消费者在打折促销时期购买,则会降低该期间的服装售价p2;若消费者讨厌等待,则倾向于在新品发布时入手,于是新品上市期的市场需求q1增加,打折促销期的市场需求q2减少。显然,随着时尚价值敏感系数β的增大,线上零售商新品上市期的利润π1大幅增加,打折促销期的利润π2缓慢下降,整体来看,某服装的整个销售周期内线上零售商的总利润π0增加。此外,消费者对服装的时尚价值敏感系数β可以反映新品上市期的服装类型,β越大说明该服装的时尚价值越高,这类服装通常为流行款。若上市的新产品为流行款服装,包含众多时尚元素,线上时尚服装零售商应当将打折促销期间的折扣设置在较小的数值范围内,以此获取更大的利润。 服装的功能价值敏感系数α对线上零售商运营指标的影响如图3所示。 图3 服装功能价值敏感系数α对线上零售商运营指标的影响Fig.3 Influence of functional value sensitivity coefficient α on online retailer’s operational metrics 观察图3不难发现,随着消费者对服装的功能价值敏感系数α增大,消费者感知价值中功能价值的作用越来越大,因此零售商应当选择将新品上市期的服务水平s设置在较低程度。换言之,消费者对服装的功能价值敏感系数α可以反映服装的类型,α越大,说明该服装功能价值越高,由此可以判断该类服装通常为基础款或者经典款。若上市的新产品为基础款或者经典款服装,线上零售商则应将打折促销期间的折扣设置为一个较大的数值,通过低价策略吸引顾客在库存清仓处理时购买。 单位订购成本c对线上零售商运营指标的影响如图4所示。 图4 单位订购成本c对线上零售商运营指标的影响Fig.4 Influence of unit order cost c on online retailer’s operational metrics 观察图4可以发现,单位订购成本c增加,线上零售商的服务水平s以较低的增长速率提升,线上零售商在产品生命周期的大促销阶段打折力度越大,整个销售周期内线上零售商的总利润π0减少。因此,时尚服装的运营管理中要注意订购成本控制的重要性,降低服装的单位订购成本是不容忽视的。 体验服务成本系数η对线上零售商运营指标的影响如图5所示。 图5 体验服务成本系数η对线上零售商运营指标的影响Fig.5 Influence of experience service cost coefficient η on online retailer’s operational metrics 观察图5不难发现:随着体验服务成本系数η增加,在时尚服装刚上市时,线上零售商提供的虚拟试衣等体验服务水平s会降低,这样才能减少其服务成本的支出进而增加收益;服装的时尚性随着时间流逝而降低,此时服装线上零售商会进行清仓处理,设置的价格折扣越大,线上时尚服装零售商在整个产品销售周期内的总利润π0提高的程度越显著。 本文基于时尚服装销售周期特征,综合考虑了策略型消费者和体验服务,分别建立新品上市期和打折促销期的消费者效用函数并据此推导需求,从而构造零售商利润模型,分析线上零售商存在最优运营策略的条件,以及主要参数对最优解的影响。研究发现:当体验服务成本系数的取值范围满足某种条件的情况下,时尚服装线上零售商可以根据均衡解制定运营策略实现收益最大化的目标;线上零售商应当针对新上市的服装款式提供不同的服务并制定促销期的价格折扣;线上零售商在时尚服装的运营管理中还要注意订购成本的控制,尽量降低单位服装的订购成本。因此,时尚服装企业应根据消费者的特点进行上架产品的选择,优化服务决策和价格制定,从而提升运营绩效。
2.2 需求函数

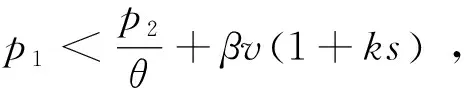
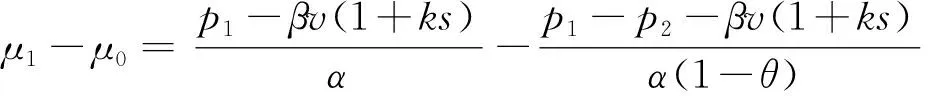
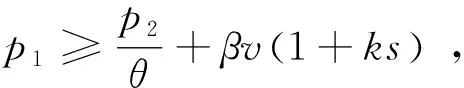
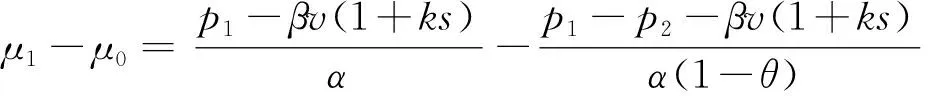
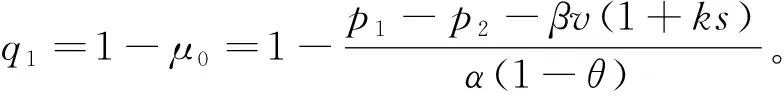

2.3 线上零售商利润函数
3 模型求解及分析
3.1 打折促销期线上零售商最优定价策略

3.2 新品上市期线上零售商最优定价和服务策略

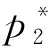

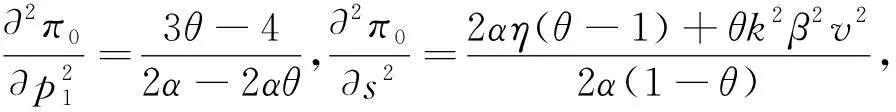
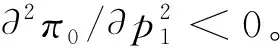


3.3 模型分析
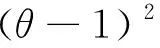



2α(1-θ)[η(4-3θ)+4k2βv(1-θ)]
2α(1-θ)[η(4-3θ)+4k2βv(1-θ)]4 算例分析


5 结 语

