基于社交圈的信息分享策略研究*

章 迪，潘 理

（1.上海交通大学 电子信息与电气工程学院，上海 200240；2.上海市信息安全综合管理技术研究重点实验室，上海 200240）

0 引 言

随着互联网技术的不断发展，社交网络中的用户越来越多，社交网络成为人们日常生活中必不可少的一部分。比较有名的社交网络平台有Facebook、Twitter、微信等。用户使用社交网络的主要目的是结识更多朋友，实现信息分享，提高交流的效率，这样用户就会在社交网络中分享大量个人信息。如果这些信息被不法分子恶意传播利用，就会使得用户个人信息受损。比如，人们经常会在社交网络平台上分享个人状态、个人信息，这些敏感信息如果被恶意用户获得，就可能会导致电话诈骗、身份欺诈等各种危险。

针对社交网络隐私保护问题，主要采用社交网络的访问控制技术，主要有基于属性的访问控制模型[1]、基于信任的访问控制模型[2]、基于语义的访问控制模型[3]、基于关系的访问控制模型[4-5]和基于角色的访问控制模型[6]。对于在保护用户个人隐私的前提下如何分享个人信息充分使用社交网络的需求，已有的方法已经不能够适用。个人网络社交圈的划分有：SQUICCIARINI等人采用共同兴趣属性进行朋友圈群体的分类[7]；Hu和Yang提出了一个新型的个人网络朋友圈划分算法[8]，通过为每一条边构建属性，将节点信息和网络结构结合在一起；YOUSHIDA提出了通过属性图进行朋友圈划分的算法[9]，属性图是由用户属性构建的规则化的图结构；MACAULEY等人提出了无监督学习算法来基于额外的用户信息发现个人网络中的潜在圈子[10]。当前，已存在社交网络中对隐私保护的信息分享研究有基于收益和分享自适应信息分享策略[11-12]，即通过一条信息的具体内容带来的收益和风险判断该条信息是否分享。但是，这种方法需要消耗大量的时间，且对于社交网络中大量的用户，对所有用户进行逐一配置，不仅工作量巨大，而且往往达不到效果。

解决社交网络中用户的个人信息隐私安全问题，存在的困难有两点：一是需要管理中心用户的好友数量越来越多，面对大量的个人好友，如何方便进行策略自动化配置和管理；二是如何设置合适的信息分享策略，保护用户个人的隐私安全，同时使得用户将信息分享给更多的人，不会因为隐私问题限制对社交网络的使用。面对这些问题，本文设计了基于社交圈的信息分享策略方法，满足社交网络中用户在分享信息时对隐私保护的需求。

本文的研究思路分为两个部分。第一部分是基于密度聚类的社交圈划分算法，通过将个人网络中好友划分到不同的社交圈便于好友管理，简化信息分享时的配置。本文的社交圈划分算法可以划分出个人网络中的特殊节点——桥梁节点。桥梁节点连接了各个社交圈，同时隔离社交圈之间的直接联系，减少社交圈之间的信息传播，提高社交圈之间的独立性，避免社交圈之间的信息传播对用户造成隐私泄漏。第二部分是在社交圈划分的基础上，提出了一种信息分享策略，即选择不同社交圈分享信息，解决用户对分享信息和隐私安全之间的矛盾，将用户分享信息问题转化为数学中的0-1背包问题求解，既保障了用户的隐私意识需求，又促进了社交网络的信息分享最大化。

1 社交圈划分算法

1.1 基本定义

社交 网络可以抽象为图模型G=(V,E)，其中V代表用户节点集合，E代表相应的社交网络关系。本文主要研究对象是社交网络中的个人网络（Ego Network），是社交网络的子结构。它包含一个中心节点、相邻节点以及各个节点之间的连接关系。

个人网络Gv=(Vv,Ev)代表节点v的个人网络图结构，Vv表示节点v的一跳好友，Ev表示一跳好友之间的连接关系。

属性相似度。对于节点v,w∈Vv，feature(v)和feature(w)分别代表节点v、w的属性特征向量，用户v、w之间的属性相似度记为：

结构相似度表示两个节点v,w∈Vv在网络结构中的相似性，即两个节点共同的邻居数量占比，记为：

节点相似度。由节点的属性相似度和结构相似度通过平衡参数α组合而来，记为：

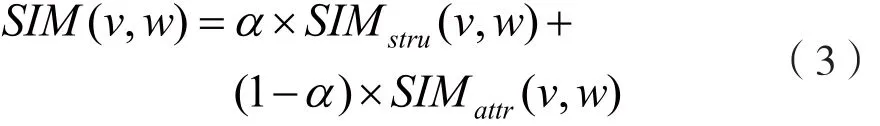
ε-邻居。对于节点v∈Vv，其ε-邻居包含与其直接相邻节点相似度大于ε的节点集合，Γ(v)表示邻居节点集合，记为：

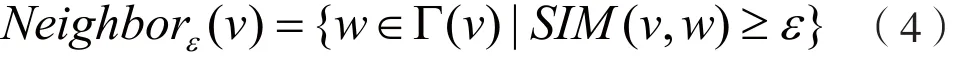
中心节点。对于节点v∈Vv，它的ε-邻居集合节点数量至少为 MinPts，记为：

直接可达。节点w在中心节点v的ε-邻居中，则称节点w由节点v直接可达，亦节点v直接可达节点w，记为：

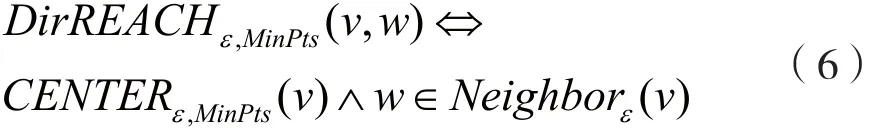
间接可达。对于节点v和w，如果存在节点序列v1,…,vn∈Vv满足v1=v,vn=w，且节点序列中相邻的节点vi直接可达vi+1，则称节点v间接可达节点w。

相互连通。对于节点v和w，如果存在一个中心节点u∈Vv，使得节点u同时间接可达节点v和节点w，则称节点v和w是相互连通的。

1.2 社交圈模型

社交圈（SC）：如果一个非空子图（SC）中的所有节点是相互连通的，且SC是满足间接可达的最大子 图，那么称SC是一个社交圈。

社交圈是定义在参数和MinPts下的，满足两个条件：（1）连通性，同一个社交圈中的所有节点是相互连通的；（2）最大化，相互连通的节点都在社交圈中。通过对网络中节点之间的间接可达关系，将同一个社交圈的节点全部划分出来。

桥梁节点（BRIDGE）。对于节点v∈Vv，如果它与两个或者两个以上的社交圈有相互连接的边，同时该节点不属于任何一个社交圈，则该节点是桥梁节点。

个人网络社交圈模型包括二部分：一是不同的社交圈SC；二是所有的桥梁节点BRIDGE。

1.3 基于密度聚类社交圈划分算法分析

基于密度聚类的社交圈划分算法（Density Based Social Circle Partition Algorithm，DBSCPA）利用不同节点之间的相似性度量和节点邻居之间的关系，根据间接可达关系推导最大连接的节点集合，是划分出来的社交圈，并识别个人网络中的桥梁节点。本文算法根据节点之间的相邻关系，加入属性内容来判断相邻关系，使得节点之间的邻居关系更加准确，容易将同一个社交圈节点划分在一起。相比于文献[9]基于属性图的方法，如果只根据属性容易将网络中结构关系不紧密的节点划分在一起，导致结果不准确。相比于文献[10]的方法，本文方法不考虑社交圈的重叠，降低了社交圈划分的复杂度，同时划分出不同社交圈之间的桥梁节点，可以减少不同社交圈之间的信息传播，有利于提高个人网络的隐私安全性。

算法过程。检查一个未划分节点是中心节点，从该节点生成一个新的社交圈，否则记为非社交圈节点。从该中心节点开始搜索所有间接可达节点，可以找到包含节点v的完整社交圈。新的社交圈ID将会赋予所有被搜索到的点。将节点v的所有ε-邻居节点插入队列中，对队列中的每一个节点，计算它的直接可达节点，并将其中未划分的节点插入队列中，不停重复，直到队列为空。对于非社交圈节点，进一步划分出桥梁节点。DBSCPA涉及3个参数——平衡参数α、相似度阈值ε和中心节点定义数值MinPts。其中，平衡参数α是用来调节属性相似度和结构相似度在整体相似度中的比例；相似度阈值ε和中心节点定义数值MinPts都是用来控制社交圈的规模。在后续实验中，平衡参数α=0.5，相似度阈值ε=0.5，中心节点定义数值MinPts=2。基于密度聚类的社交圈划分算法（DBSCPA）伪代码如下：

Input：Gv=(Vv,Ev);节点相似度表 ; ε;MinPts

Output：社交圈SC；桥梁节点BRIDGE

FOR 每一个未划分的节点v∈VvDo∶

IF v是中心节点CENTERε,MinPts(v) THEN∶

生成一个新的社交圈序号；

将节点 x∈Neighborε(v) 全部插入到队列Q中；

WHILE Q≠0 Do∶

令y是队列Q中的第一个节点；

R = { x ∈ V | D irREACHε,MinPts(y, x )}；

FOR 每一个x∈R Do∶

IF x是未划分节点或非社交圈节点

THEN∶

将当前的社交圈编号赋予x；

IF x是未划分节点 THEN∶

将x添加到队列Q中；

将y从队列Q中移除；

ELSE

将v标记为非社交圈节点；

END FOR

FOR 每一个非社交圈节点Do∶

IF∃ x , y ∈ Γ ( v)( x.c l usterID ≠ y.c l usterID)

THEN∶

v被划分为BRIDGE

END FOR

Return 社交圈SC，桥梁节点BRIDGE

2 基于社交圈的信息分享策略

中心用户u的个人网络被划分出数量为k的社交圈SC={SC1,…,SCk}和桥梁节点，其中每个社交圈对应的用户人数为N={n1,…,nk}。用户分享一条信息m，用户对该条信息的隐私泄漏容忍度为δ，并假定SCthreat群体是潜在的危险用户。如果用户自己的个人信息传播到该社交圈，将会给用户带来潜在的危险和损失。传播的信息越多，潜在的危险和损失越大。

用户在分享个人信息后，不同社交圈之间会相互传播信息，将导致信息流向潜在危险社交圈SCthreat。不同社交圈之间的信息传播能力记为PBSC(SCi,SCj)，表示社交圈SCi和SCj之间的信息传播能力。在不超过用户隐私泄漏容忍度的前提下，最大化用户分享的人数是要求解的问题。引入标记变量xi，xi=0or1表示用户是否将信息分享给社交圈SCi。当满足求解 a rgni*xi。将信息分享策略问题转化为0-1背包最优化问题：

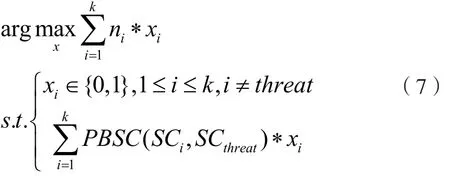
这是一个常见的NP-Hard问题，采用动态规划方法解决该问题。其中，PBSC(SCi,SCthreat)的计算公式为：

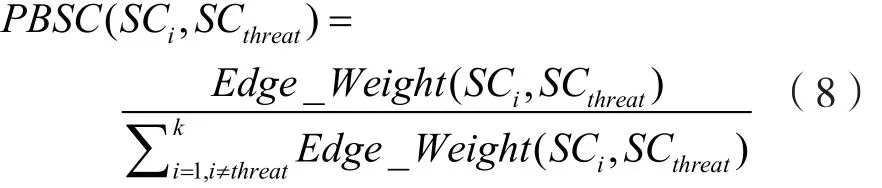
其中Edge_Weight(SC1,SCthreat)代表社交圈SCi和SCthreat之间相连接边的权值之和，并将其进行归一化，作为两个社交圈之间的信息传播能力。社交圈之间连接的边越多，信息传播能力越强，连边两端的节点相似度越大，即连边的权值越大，信息传播能力越强。

通过求解背包问题，即使得目标函数达到最大的解向量X=(x1,…,xk)，求解每一个社交圈标记变量的值，确定可以分享信息的社交圈。用户可以将信息分享到这些社交圈中，不会对隐私安全造成危险，同时分享信息的人数也是最多的。可见，在保护隐私安全的前提下，最大化地利用社交网络，使用户能在社交网络中与更多的人分享信息。

3 实验与结果分析

本文实验采用的是SNAP数据集，从文献[10]获得。本文实验利用的是Facebook的个人网络数据，包含用户节点的各种属性和网络用户之间的连边关系。本文实验的实验环境是Intel Corei7-6700 3.4G处理器，16 GB内存。

3.1 社交圈划分实验

本实验使用平衡误差率（Balanced Error Rate，BER）[10]作为评估指标， S C = { S C1, … ,S Ck}代表预测社交圈集合，SC = { S C1, … ,S Ck}代表真实社交圈集合。

下面是平衡误差率（BER）的公式：

实验评估时，因为真实与预测社交圈的数量差异，令f是预测社交圈集合SC到真实社交圈集合的部分映射。预测与真实社交圈集合的1-BER值越大，则算法效果越好，计算如下：

本文实验主要内容比较了McAuley等人的概率模型（Probability Based Social Algorithm, PBSA）[10]、Yoshida的低秩嵌入模型（Low Rank Embedding Algorithm，LREA）[9]与本文的社交圈划分算法（DBSCPA）。如表1所示，本文社交圈划分算法的1-BER值为0.78，相比低秩嵌入算法的0.59要高出很多，比概率模型算法的0.83差一点。

表1 三种算法的1-BER值

本文社交圈划分算法相对于当下比较准确的概率模型算法，在精确度方面比较接近，比其他的算法要优越。但是，本文算法还可以发现网络中扮演特殊角色的桥梁节点。正是由于识别了这些节点降低了精确度。然而，相对于精确度的损失，识别出这些节点的作用和意义更大。

3.2 基于社交圈的信息分享策略实验

实验的评价标准是在相同隐私泄漏容忍度（Tolerance of Privacy Leakage）下，信息分享授权好友占所有好友的比例。隐私泄漏容忍度指用户对该条信息泄漏给自己带来的损失所能容忍的程度。隐私泄漏容忍度越大，表示该条信息越不重要，对用户可能造成的损失越小，能够分享的人越多。实验目的是验证本文提出了信息分享策略的可行性，同时验证本文社交圈划分算法比其他划分算法在此信息分享策略上面的优势。

假定中心用户发布了9条隐私泄漏容忍度不同的消息m1,…,m9。这9条信息对应中心用户的隐私泄漏容忍度分别是δ1=0.1,…,δ9=0.9。根据不同的隐私容忍度做了9次对比实验。为了便于实验比较，假定对于每一条信息，中心用户认定的威胁用户都是同一个社交圈。

实验将本文的社交圈划分算法和概率模型、低秩嵌入算法进行对比。考虑这3种不同的社交圈划分算法对用户信息分享策略的影响，结果如图1所示。授权节点所占的比例随着隐私泄漏容忍度不断增大，即信息包含隐私内容越少，可分享的人数越多，说明本文信息分享策略是可行的。同时，概率模型和低秩嵌入模型的用户所授权人数占比都较低。本文的算法划分的社交圈相比其他两种算法，在同等隐私泄漏容忍度的情况下，授权节点占所有好友节点的比例要高，说明本文的社交圈划分算法在信息分享策略方面相比于其他划分算法具有较高的优势，更能提高社交网络的可用性。

图1 信息分享策略授权节点占比

本文社交圈划分算法将桥梁节点单独划分出来，而不是将其划分在社交圈中，使得不同社交圈之间信息传播变得困难，提高了各个社交圈之间的独立性，减少了信息传播。其他算法中，社交圈与危险社交圈之间关系紧密，信息传播较多，导致很多用户无法授权，说明本文的社交圈划分算法有利于减少不同社交圈之间的信息传播，能够在保护用户隐私的情况下，最大化分享人数，提高社交网络的可用性。

4 结 语

提出了个人网络基于密度聚类的社交圈划分算法，能够有效识别中心用户好友所属的不同社交圈，并识别出其中具有特殊角色的桥梁节点。针对社交网络中信息分享问题，本文提出了基于社交圈划分的隐私信息分享策略，将其转化为数学问题中的0-1背包问题。在保护用户隐私的前提下，选取特定的好友分享信息，使得能够分享信息的好友数量最大。最后，通过实验验证本文社交圈划分算法和信息分享策略的有效性。下一步将考虑有向网络以及关于信息内容的分析，以期完善信息分享策略。