线性时变系统的时域分析*

陈绍荣，何 健，刘郁林，朱行涛

（1.陆军工程大学 通信士官学校，重庆 400035；2.军委装备发展部军事代表局驻成都地区军事代表室，四川 成都 610041；3.重庆市经信委，重庆 400015）

0 引 言

在国内外《信号与系统》中[1-2]，均提到了连续时间线性系统可分为线性时变系统和线性时不变系统。然而，连续时间线性系统的时域分析都局限于介绍线性时不变系统的分析方法。原因有两点，一是并非所有描述线性时变系统的线性变系数微分方程都有解；二是即使描述线性时变系统的线性变系数微分方程有解，也难以找出系统全响应的通解公式。本文在文献[3]的基础上，研究了一阶线性时变系统的时域分析问题，采用降阶解法给出了一类可解的二阶线性时变系统全响应的通解公式，解决了一类可解的高阶线性时变系统全响应的时域求解问题。

1 一阶线性时变系统全响应的通解公式

设描述一阶线性时变系统响应y(t)与激励f (t)关系的微分方程为：

利用乘积求导法则，对式（2）左边作逆向改写，可得：

对式（3）两边作不定积分，可得：

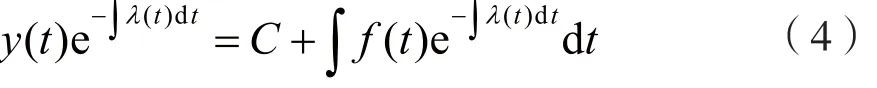
由式（4）可得一阶线性时变系统的全响应y(t)的通解公式，即：

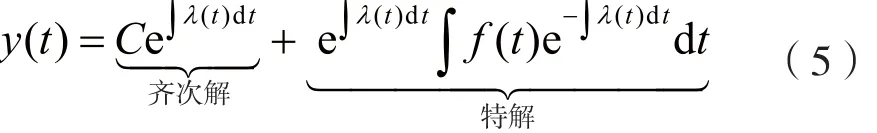
式中，C为任意常数。

2 二阶线性时变系统全响应的通解公式

设描述二阶线性时变系统响应y(t)与激励f(t)关系的微分方程为：

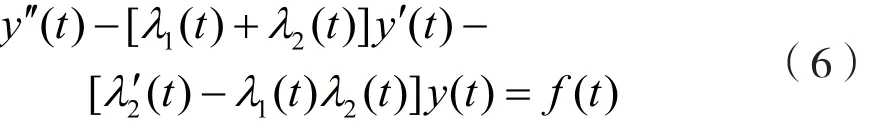
其实，描述二阶线性时变系统的非齐次微分方程式（6）可改写成：

为了采用降阶解法，现定义新变量x(t)，即：

考虑到式（8），则二阶线性变系数非齐次微分方程式（7）降成了一阶线性变系数非齐次微分方程，即：

考虑到通解式（5），则描述一阶线性时变系统的非齐次微分方程式（9）的通解x(t)，可写成：

式中，C1为任意常数。

考虑到通解式（5）和通解式（10），则一阶线性变系数非齐次微分方程式（8）的通解，即式（6）描述的二阶线性时变系统的全响应y(t)的通解公式可表示为：

式中，C1和C2为任意常数。

3 线性时变系统的时域分析举例

3.1 例子1

例1：设描述一阶线性时变系统响应y(t)与激励f(t)关系的微分方程为：

若系统的激励f(t)=e-sint-tε(t)，系统的初始状态y(0_)=2，试求系统的零输入响应yx(t)、零状态响应yf(t)及全响应y(t)。

3.1.1 方法1

解：利用通解式（5）直接进行求解。由微分方程式（12）知道，λ(t)=-cost。考虑到通解式（5），则有：

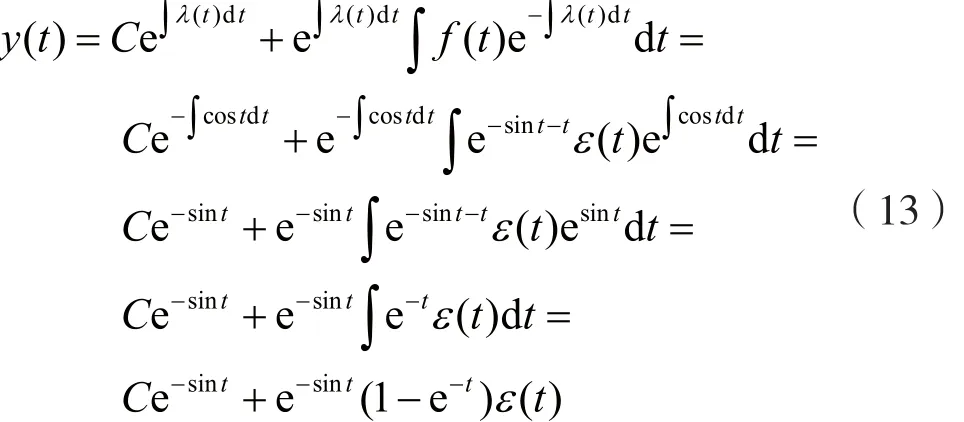
式中，C为任意常数。

考虑到系统的初始状态y(0_)=2，由式（13）可得y(0_)=C=2。于是，系统的全响应y(t)为：

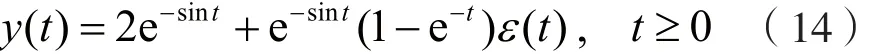
显然，系统的零输入响应yx(t)和零状态响应yf(t)分别为：

3.1.2 方法2

采用上限积分法求解。

将系统的激励f(t)=e-sint-tε(t)代入非齐次微分方程式（12），可得：

将式（17）两边乘以esint，可得：

利用乘积求导法则，对式（18）左边作逆向改写，可得：

由式（19）可得：

在τ∈[0_,t]区间上，对式（20）两边积分，可得：

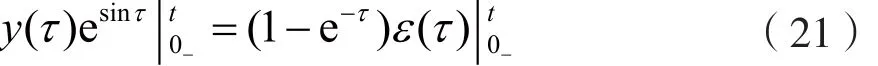
考虑到系统的初始状态y(0_)=2，由式（21）可得：

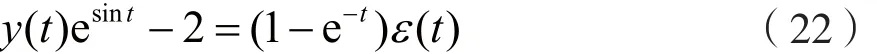
于是，系统的全响应y(t)为：

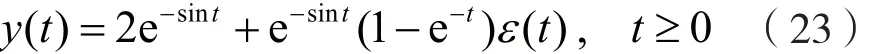
显然，系统的零输入响应yx(t)和零状态响应yf(t)分别为：

3.2 例子2

例2：设描述二阶线性时变系统响应y(t)与激励f(t)关系的微分方程为：

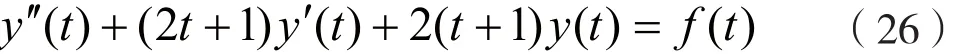
若系统的激励 f(t)=2e-tε (t)-δ(t)，系统的初始状态y(0_)=2，y'(0_)=0，试求系统的零输入响应yx(t)、零状态响应yf(t)及全响应y(t)。

3.2.1 方法1

利用通解式（11）直接进行求解。

其实，描述二阶线性时变系统的非齐次微分方程式（26）可写成：

将微分方程式（26）与微分方程式（7）比较，可知：

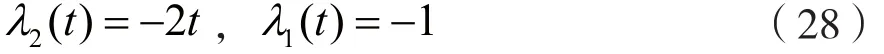
为了计算方便，令：

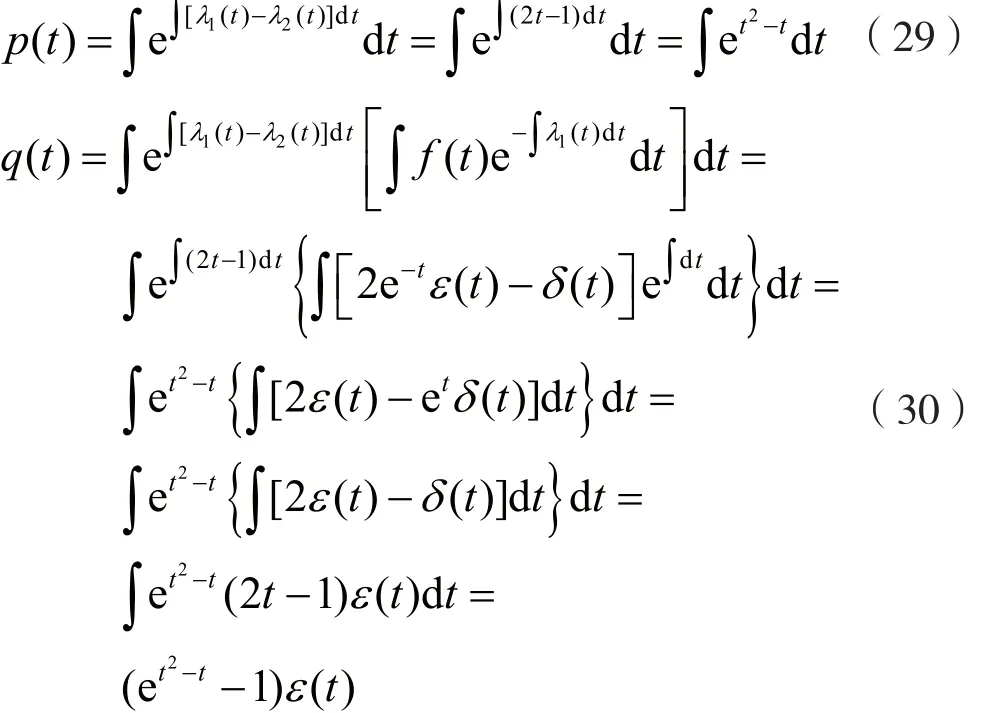
考虑到式（29）、式（30），则通解式（11）可写成：

考虑到式（29），由式（31）可得：

由式（32）可得：

由式（31）可得：

将C1=0、C2=2代入式（31），可得系统的全响应y(t)，即：

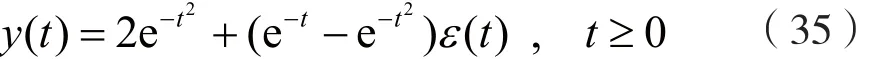
显然，系统的零输入响应yx(t)和零状态响应yf(t)分别为：

3.2.2 方法2

采用上限积分降阶法求解。

将系统的激励f(t)=2e-tε(t)-δ(t)代入非齐次微分方程式（27），可得：

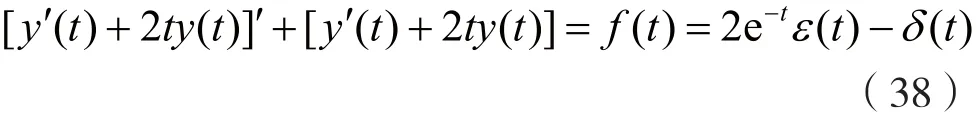
将式（38）两边乘以et，可得：

利用乘积求导法则，对式（39）左边作逆向改写，可得：

由式（40）可得：

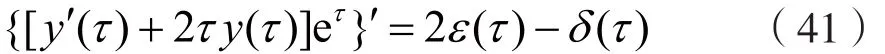
在τ ∈[0-,t ]区间上，对式（41）两边积分，可得：

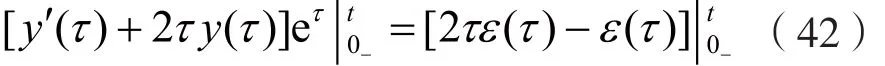
考虑到系统的初始状态 y (0-) = 2， y ′(0-)=0，由式（42）可得：

即：

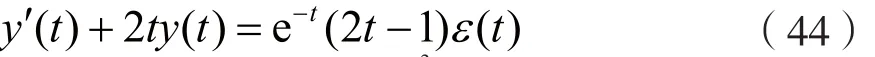
将式（44）两边乘以et2，可得：

利用乘积求导法则，对式（45）左边作逆向改写，可得：

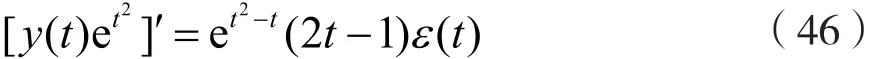
由式（46）可得：

在τ ∈[0-,t ]区间上，对式（47）两边积分，可得：

考虑到系统的初始状态 (0) 2 y-= ，由式（48）可得：

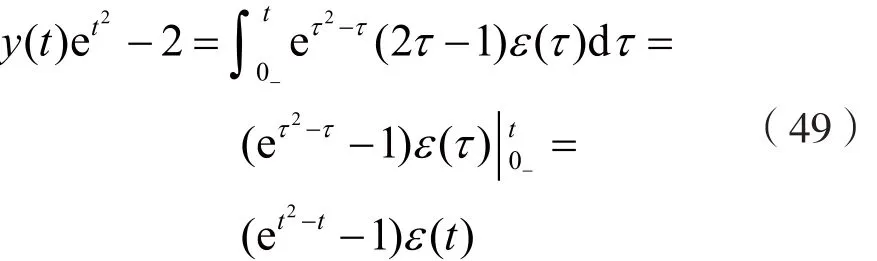
于是系统的全响应 ()y t为：

显然，系统的零输入响应 yx( t)和零状态响应yf(t)分别为：

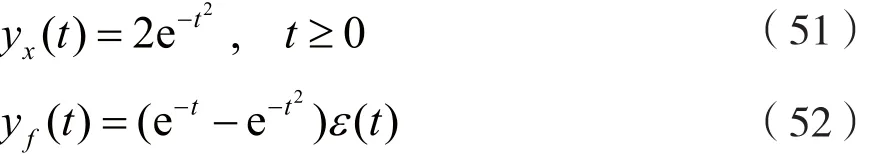
4 结 语

本文基于分离变量的基本思路，巧妙地在微分方程两边乘以同一函数，利用乘积求导法则，将方程的左边逆向改写成乘积求导形式，再对方程两边作不定积分，最后通过分离变量导出一阶线性时变系统全响应的通解公式。基于一阶线性时变系统全响应的通解公式，采用降阶解法导出了一类可解的二阶线性时变系统全响应的通解公式。这不仅揭示了线性变系数非齐次微分方程的解结构，即齐次解加特解，而且解决了一类可解的高阶线性时变系统全响应的时域求解问题。