特大型直齿锥齿轮直廓变切深加工理论及验证

张波，李家琦，张宁，张亚双

(1.河南科技大学 机电工程学院，河南 洛阳 471003；2.中国航发沈阳黎明航空发动机有限责任公司，辽宁 沈阳 110043)

0 引 言

传动齿轮是机械产品的核心零件，具有传动效率高、使用寿命长等优点，在制造业中占有重要地位。作为一种特殊类型的齿轮，直齿锥齿轮主要用来传递相交轴之间的运动和动力[1-5]。近年来，随着大型发电设备、大型船舶重工制造、矿山钻探和海洋工程等重工业行业的飞速发展，特大型直齿锥齿轮的需求急速上升[6]。国外的特大型直齿锥齿轮加工技术一直处于领先水平，并对齿轮加工机床形成垄断趋势，严重阻碍了我国相关行业的发展,因此,对特大型直齿锥齿轮的加工方法研究具有重要意义。传统的展成刨齿法加工特大型直齿锥齿轮，由于刀具回转半径大，加工机床会占用大量空间，且加工效率低，加工成本高。因此，有必要研究更加经济有效的加工方法。

针对直齿锥齿轮的加工方法问题，一些专家和研究人员提出很多独到的见解：曹泉利等[7]提出采用经过改装的牛头刨床加工大模数直齿锥齿轮，适用于小企业小批量生产；徐恺等[8]提出直廓内齿轮行星轮系代替渐开线内齿轮行星轮系在工业上是完全可行的；徐恺等[9]提出直廓内齿轮代替渐开线内齿轮在加工精度、加工效率和加工成本上都有独特的优势；赵志礼[10]提出采用指形铣刀加工直齿锥齿轮，提出一种啮合方向上齿形误差的计算方法；冀晓红等[11]提出以计算机数控(CNC)系统代替普通滚齿机中的机械传动链，建立统一的齿轮加工数学模型，并在计算机上实现任意齿形齿轮的模拟加工；徐晨影[12]提出运用EDM线切割机床加工直齿锥齿轮，可以解决大型直齿锥齿轮加工精度问题，但加工成本高且效率低；温淑华等[13]研究了铣刀模数的选择方法，总结了中间模数法和设计配对法对齿形偏差量的影响。

上述研究成果为研究特大型直齿锥齿轮的加工方法、铣刀模数选型、提高齿轮加工效率提供了理论基础，可以尝试采用直廓齿面代替渐开线齿面、成形法铣齿来加工特大型直齿锥齿轮。因此，本文提出一种新方法即直廓变切深加工理论：大轮齿面以直廓铣刀代替传统的渐开线铣刀进行变深度铣齿加工。直廓铣刀材料采用硬质合金刀片，刀片制造简便，更换方便且耐热性能好，适合高速铣削，提高加工效率。渐开线铣刀材料一般为高速钢，耐热性能差，廓形加工难度大，且刀具磨损后需要人为修正刀廓，直接影响加工精度。所以直廓铣刀相比于渐开线铣刀在实际加工中更有优势。由大轮完全共轭出小轮后，对小轮进行齿面拓扑修形并进行啮合分析。通过实际的加工对滚验证，证明了直廓变切深加工理论的正确性及其可行性。

1 变深度加工原理

锥齿轮的啮合运动轨迹是空间上的球面渐开线，为了研究方便，一般是从锥齿轮的背锥上展开，以当量齿轮的平面渐开线代替球面渐开线。采用指形刀加工齿轮时，以不同锥距处当量齿轮的标准齿形作为加工的基准齿形。通过主轴带动铣刀转动，包络出齿槽廓形。为减小加工误差，加工过程中铣刀的回转中心线要垂直于直齿锥齿轮的节锥线，为了排屑方便，进刀方向为从齿轮的大端到小端。由于大端和小端之间的渐开线模数不同，如果只沿齿轮节锥线进给，不能得到需要的齿形面。为了得到与基准齿形相近的齿形面，可以控制指形铣刀在节锥线的基础上进刀或退刀，保证加工出的齿槽宽与基准齿槽宽一致，以达到传动的精度要求和传动比要求。加工时铣刀进给方向如图1所示。

图1 铣刀进给方向示意图

根据单刀双面法切齿原理，进行铣刀设计。铣刀以大轮齿长中点模数处当量齿轮的齿形为基准齿形设计，在加工过程中保证任意锥距处分度圆齿厚与铣刀分度圆齿厚相等，从而计算出铣刀的进退刀深度K。为了铣刀设计方便，仅对铣刀实际工作的刀刃部分进行设计分析。铣刀参数如图2所示。

图2中：ha为铣刀的齿顶高；hf为铣刀的齿根高；S为铣刀的分度圆齿厚；Sa为铣刀齿顶厚；ei为铣刀的任意分度圆处齿厚；ri为铣刀任意分度圆齿厚到齿顶的距离。

图2 铣刀参数设计

由于直齿锥齿轮沿齿长方向某点截面的齿形可以由背锥上的齿形近似代替，故任意截面即为模数已知的平面渐开线，在该截面处分度圆齿厚

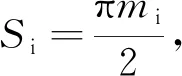
(1)

式中：Si为某一截面处分度圆齿厚；mi为该截面处当量齿轮模数。

又因为在分度圆上齿槽宽与齿厚相等，该截面分度圆齿槽宽为

(2)

由变深度加工原理可以得到

e=ei，

(3)

求解式(3)，得到该截面处ri的值，由计算式Ki=ri-ha即可求得铣刀在变深度加工过程中的进退刀深度。最终推导公式可表示为

(4)

式中，α=20°。

以13-88齿直齿锥齿轮为例进行进退刀深度计算，齿轮参数如表1所示。

表1 齿轮几何参数

将齿轮沿齿长方向均匀分成8份共9个齿形截面，计算每一齿形截面处的切削深度变化量，拟合出曲线如图3所示。

规定：Ki<0时表示退刀；Ki>0时表示进刀。根据拟合出的曲线可以看出，从齿长中点位置往小端加工时，在节锥线的基础上退刀；往大端加工时，在节锥线的基础上进刀。进退刀是为了保证分度圆锥上齿宽和齿槽宽一致，使齿轮副满足强度要求[14]。

图3 进刀深度拟合曲线

2 齿面方程求解

2.1 直廓变切深大轮产形面方程求解

由直廓变切深加工原理，建立如图4所示的铣刀坐标系。

图4 铣刀坐标系

图4中:Xp为铣刀回转中心线到直线型刀刃顶端的距离；rt为刀刃上任意一点；SP为刀刃的长度；α为刀刃的倾角；L为铣刀分度圆齿厚中点到齿顶的距离；Y轴为铣刀的加工方向。由上述进退刀深度推导出的公式可知，铣刀的加工轨迹即为拟合出的Ki曲线。

由图4可知，大轮加工过程中产形面矢量方程可表示为

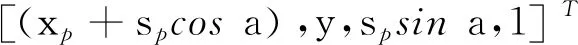
该产形面方程即可表示为大轮的齿面方程r2(sp2y2)。

2.2 共轭小轮齿面求解

在齿轮啮合坐标系中，大、小轮啮合和位置关系如图5所示，Sm(Xm，Ym，Zm)为固定坐标系，

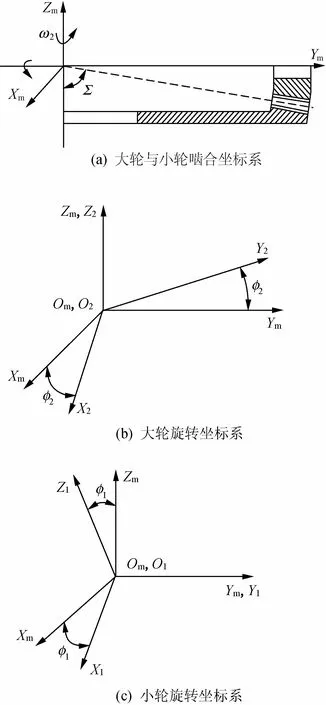
图5 啮合坐标系

∑=90°为轴交角，ω1为小轮角速度，ω2为大轮角速度，S1(X1，Y1，Z1)与小轮固定连接在一起，S2(X2，Y2，Z2)与大轮固定连接在一起，在传动过程中，小轮转角φ1与大轮转角φ2满足传动关系

(6)

式中：φ′2和φ′1为大小轮初始转角；Z1为小轮齿数；Z2为大轮齿数。在齿轮啮合运动关系基础上，大小轮满足啮合方程

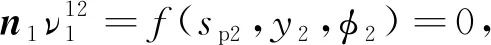
(7)

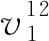
基于平面产形轮原理，以大轮作为产形轮，小轮作为被加工齿轮对小轮齿面进行求解。小轮的齿面方程和单位法矢求解如式(8)所示，

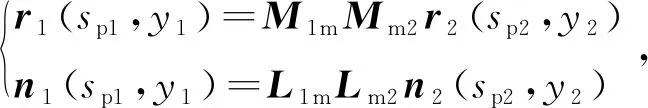
(8)

式中：M1m为机床固定坐标系Sm到小轮坐标系S1的变换矩阵；Mm2为大轮坐标系S2到机床固定坐标系Sm的变换矩阵，L1m、为M1m、的转动子矩阵，矩阵表达式为

2.3 小轮齿面修形及传动误差分析

理论上，完全共轭的齿轮副啮合方式为齿长方向的线接触。但装配误差、齿面受力变形等因素会影响啮合效果，造成轮齿边缘接触，导致齿面应力不均衡，严重影响齿轮寿命。所以在实际应用时，需要对齿面进行适当修形，使得齿轮副由线接触变为局部点接触，以均衡齿面载荷。

用Σ1表示小轮未修形齿面，对应矢量方程为r1(sp1，y1)，单位法矢n1(sp1，y1)；用Σ0表示修形后的齿面，对应的矢量方程为r0(sp1，y1)。未修形齿面Σ1与修形后齿面Σ0之间的偏差量可写为

Δδ(sp1，y1)=[r0(sp1，y1)-r1(sp1，y1)]·

n1(sp1，y1)，

(9)

这是一个误差曲面方程，泰勒展开后可以用二阶曲面近似表示为

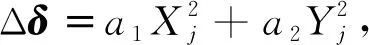
(10)

式中：Xj为小轮旋转投影后齿长方向坐标；Yj为旋转投影后齿高方向坐标[15]；a1为齿长修正系数；a2为齿廓鼓形量修正系数。通过对各系数的设置和组合，可以构建各种形状的齿面拓扑图。

未修形的齿轮副啮合方式为沿齿长方向上的线接触，即齿轮副在接触迹线上存在无数个接触点，进行传动误差计算时存在多解性，为了计算方便，增加一个啮合点控制方程，

(11)

式中：Re为小轮的大端锥距；b为小轮的齿宽。式(11)用于计算齿轮副在任意转角啮合时接触迹线位于齿宽中点位置的解。

3 算例分析

以表1的直齿锥齿轮为例，对小轮进行齿面修形和传动误差分析。

用MATLAB编写小轮修形程序和修形后小轮与大轮TCA程序，选取修形系数a1=0.000 01，a2=0.000 01，进行齿面综合修形。小轮齿面拓扑图和传动误差分析如图6所示。

图6 齿面啮合分析结果

赋值a1和a2进行综合修形，由图6可以看出：进行综合修形后，小轮大端和小端的偏差量Δδ约为0.35 mm，齿顶和齿根的偏差量Δδ约为0.05 mm。偏差量由两边向齿面中心位置逐渐减小，齿面接触方式由理论的线接触方式变为齿面中心位置的点接触方式，调整了齿面接触区域，减小边缘接触对齿面的损坏。同时改变齿轮接触应力不均衡的现象，使齿面载荷分布集中于齿面中点位置，增加齿轮寿命。通过赋值不同的修形系数，优化出最适合实际工作需求的接触方式，可以达到改善齿面接触性能的目的。

4 加工及滚检试验

为了验证此种加工方法和修形方法的正确性，进行加工和对滚试验。大轮和小轮可以在带分度头的专用铣床上加工。图7为大轮的铣齿试验，图8为大轮和小轮的滚检试验。

将大轮齿坯装夹在回转工作台上，进行精确对中并固定。将铣刀回转轴线调整到与齿坯分锥线垂直的位置并进行对刀，然后在自动编程模块中输入求得的各个切深变化量值，开始加工。

对小轮修形后进行啮合试验，在小轮齿面上涂满红丹粉，用于啮合时沾染。选取小轮为主动轮，回转工作台卸荷，小轮以0.15 rad/s的转速与 大轮进行啮合，当大轮齿面上红丹粉沾染面积基本不变时，啮合试验结束。啮合试验完成后，观察齿面红丹粉沾染情况，判断啮合效果。

图7 加工直齿锥齿轮

图8 对滚试验

可以看出，小轮修形后，滚检试验接触区为齿面中心区域的位置，与理论啮合分析结果基本一致，接触方式由理论的线接触变为瞬时点接触，证明此种拓扑修形方法具有可行性。

5 结 论

(1)针对特大型直齿锥齿轮加工质量差、加工效率低的问题，提出直廓、变切深加工理论，提高加工效率，减少加工成本。

(2)针对与大轮完全共轭的小轮提出一种齿面拓扑修形方法，通过改变2个齿面修形参数实现对齿面拓扑修形的自由控制，根据实际需要改变齿面啮合性能。

(3)理论分析和实际切齿滚检试验验证了本文提出方法的正确性和可行性。