基于双因子混合加权相似度的协同过滤推荐算法

王留芳，刘镇镇，魏蓝，吴正江

(1.河南理工大学 计算机科学与技术学院，河南 焦作 454000；2.鹤壁汽车工程职业学院 电子工程系，河南 鹤壁 458030；3.厦门大学 信息学院，福建 厦门 361005)

0 引 言

近年来，关于高校图书馆图书个性化推荐[1]算法很多，主要有基于用户的协同过滤推荐算法[2]、基于知识的推荐算法[3]，基于内容的推荐算法[4]、混合推荐算法[5]等。其中，基于用户的协同过滤推荐算法是应用比较成功的一种算法，它的基本思想是寻找与目标用户兴趣相似的邻居用户[6]，然后把邻居用户感兴趣的项目推荐给目标用户。它的优势是把用户分成近邻和非近邻，推荐准确度高，能够发现用户潜在兴趣，个性化程度高。但是存在以下问题：一、数据稀疏问题。当图书资料较多、借阅读者较少时，出现用户之间兴趣的相似度不准确问题，或者不同读者之间借阅的图书资料重复率较低时，无法找到相似近邻用户；二、冷启动[7问题。它是基于用户对项目的历史评分来预测推荐，当新书刚录入推荐系统，没有读者对该图书评分，或者当新生读者刚加入系统时，没有对图书评分，所以无法预测评分，导致推荐结果不准确。

针对以上问题，本文在修正余弦相似度算法的基础上引入基于用户属性的相似度算法，并将两者加权混合，该算法充分利用用户属性不受数据稀疏和冷启动影响的优势，避免了传统计算方法的缺点，并通过实验验证该算法的准确性。

1 传统的相似度算法

基于用户的协同过滤推荐算法重要步骤就是计算用户之间的相似度，相似度公式不同，相似度值也会不同。目前，用户之间的相似度计算方法主要有余弦(cosine)相似性[8]、皮尔逊相关系数(Pearson correlation coefficient)相似性[[9]、修正余弦相似度等[10]，如式(1)～(3)所示。

(1)

(2)

simcc(u，v)=

(3)

下面用一个例子说明几种相似度计算方法的缺点，表1是一个User-Book评分矩阵[11]，有3个用户，分别是user1，uer2，user3，4本书，分别是book1，book2，book3，book4，表2～4给出使用3种相似度计算方法得到的用户间的相似度。

表1 用户评分矩阵

表2 余弦相似度

表3 皮尔逊相关系数相似度

从表2～4可以看出，采用以上3种相似度计算公式存在以下问题：

(1)对相似度较低的用户得出的相似度较高。例如表1中user1和user3对book1和book2的评分为(4，3)和(2，1)，两者对book1和book2的喜好可能相反，而表2中user1和user3的相似度为0.975，表3中user1和user3的相似度为0.892，说明在数据稀疏的情况下，用余弦相似度算法和皮尔逊相关系数相似度算法，使原本较低相似度的两个用户呈现出较高的相似度。

表4 修正余弦相似度

(2)对相似度较高的用户得出较低的相似度。例如表1中，user1和user2的评分向量分别为(4，3，5，4)和(4，3，3，4)，两者相似度极高，而表3用皮尔逊相关系数相似度算法得出的相似度为0，表4修正余弦相似度算法得出的相似度为-0.316，使原本较高相似的两个用户，计算结果较低。

以上例子说明，在数据稀疏的情况下，用传统相似度算法得到的相似度不准确，导致推荐结果精度不高。

2 本文相似性算法

为了提高推荐结果的精度，本文引入阈值、双因子，基于用户属性的相似度算法，提高传统相似度算法的准确性。

2.1 阈值定义

阈值是判断目标用户和其他用户数据是否稀疏的一个临界值，初始值为平均借阅量，阈值初始值会随着平均借阅量的变化而变化，所以阈值要阶段性(一周或一个月)寻优。当读者的借阅量小于阈值时，存在数据稀疏问题，阈值的公式为

TDn=TDn-1±[TDn-1/5]·J，

(4)

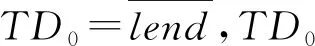
2.2 双因子定义

引入双因子，是为了在数据稀疏的情况下，自动调整传统相似性算法与基于用户属性相似算法的权重，双因子使用sigmoid函数定义，假设a，b为双因子，其公式为

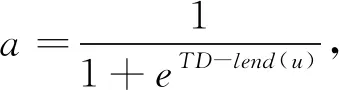
(5)

(6)

式中：a为目标读者u的数据稀疏权重；lend(u)为目标读者u的借阅量；TD为阈值；b是近邻读者v的数据稀疏权重；lend(u)为读者v的借阅量。

2.3 基于读者属性的相似度算法

基于读者属性[12]的相似度算法是以读者的属性为参数，读者属性越相似读者的偏好就越接近，不存在数据稀疏和冷启动问题。

读者属性主要包括读者卡号、身份证、姓名、年龄、密码、专业、学院、注册日期、性别、年级等。读者属性相似度计算公式为

simattr(u，v)=∑i∈attr(i)wi·attr(u，v，i)，

(7)

式中：wi为读者u和读者v的第i个属性权重；attr(u,v,i)为第i个属性的相似度。

2.4 双因子混合相似性算法

从文献[5]实验可知：皮尔逊相关系数相似性算法simp(u，v)和修正余弦相似度算法simcc(u，v)误差较低，但是，相比之下simcc(u，v)算法误差曲线比较平滑，最大值与最小值之间的差值较小，所以，选择simcc(u，v)与基于读者属性的相似度算法加权混合形成一种新的相似度算法simtfcc(u，v)，公式为

simtfcc(u，v)=(1-a)(1-b)simattr(u，v)+

absimcc(u，v)。

(8)

从公式(5)、(6)可以看出，a,b的值随着阈值与读者借阅的差值变化而变化。当读者借阅量lend(u),lend(v)与阈值TD相等时，a,b的值均为0.5，当lend(u),lend(v)的值大于阈值时，即读者借阅量不稀疏时，修正余弦相似度算法simcc(u,v)的权重增加，当lend(u),lend(v)的值小于阈值时，即读者借阅量稀疏时，基于读者属性相似性算法simattr(u,v)权重增加。

2.5 最终预测推荐算法

为目标用户预测推荐，使用文献[4]中的协同推荐公式

2.6 算法描述

(1)输入读者姓名或读者ID。

(2)根据公式(4)计算阈值TD，阈值寻优。

(3)根据公式(5)～(6)计算双因子a，b的值。

(4)根据公式(8)计算输入目标读者和其他读者的相似性。

(5)根据读者之间的相似度大小，选取前top_k近邻[13]。

(6)根据近邻读者的偏好，预测目标读者的偏好图书评分。

(7)根据公式(9)，选取推荐结果。

3 结果与分析

3.1 实验环境

以高校图书馆读者借阅数据为数据集，共包含11 870个读者对352 597册书的107 272借阅信息量。读者属性中对读者相似性影响的信息包括专业、性别、年级、年龄等，根据参考文献可知：读者的属性权重影响从大之小依次是专业(权重为μ1=0.4)、年级(权重为μ2=0.3)、性别(μ3=0.2)、年龄(μ4=0.1)，且μ1+μ2+μ3+μ4=1。

3.2 评价标准

评分预测常用的评价指标有均方根误差[14](root mean square error，RMSE)和平均绝对误差[15](mean absolute error，MAE)，在协同过滤中RMSE用来检测预测的评分与真实测试集中的评分偏离程度，相对于MAE而言，加大了误差惩罚力度。RMSE的偏离程度越大，推荐的质量越差，推荐准确度越低。公式为

(10)

3.3 实 验

3.3.1 阈值寻优实验

由公式(5)～(6)可知，双因子的值是由阈值的大小和读者借阅量决定的，由公式(4)可知,阈值的初始值是读者的平均借阅量。随着借阅量的变化，初始阈值也会发生变化，所以要对阈值进行阶段性寻优。最优阈值是保证推荐结果正确性的前提条件。

图1 双因子混合相似度simtfcc(u，v)算法的推荐结果

从图1可以看到，使用双因子混合相似度simtfcc(u，v)推荐算法，在近邻数20～25间，阈值TD=8时，RMSE最小，推荐效果最好，所以下面的实验中取阈值[17]为8。

3.3.2 与传统相似度比较

在双因子相似性[18]计算公式(8)中，根据以上实验取阈值TD=8，表1中，读者的借阅量为4本书，当读者的借阅量小于阈值8时，存在数据稀疏问题，在此情况下，对表1进行相似性计算，结果如表5所示。

从表5可以看出，在数据稀疏的情况下，改进后的相似性算法已经克服了传统相似性算法的弊端，提高了相似度计算的准确性。

表5 双因子混合相似度算法(1)

在冷启动的情况下，TD=8，目标读者的借阅量lend(u)为0，代入公式(5)中，得到a的值大约等于0，这时修正余弦相似性算法的权重ab大约为0。

双因子混合加权相似度算法变为simtfcc(u，v)=simattr(u，v)，此时对表1进行相似度计算，结果如表6所示。

表6 双因子混合相似度算法(2)

从表6可以看出，在冷启动的情况下，利用改进后的相似度算法得到的相似度与实际的相似度是一致的，克服了传统相似度不准确的问题。

3.3.3 与传统的推荐算法比较

本实验选取阈值为8时双因子混合相似度推荐算法与3种传统相似度推荐算法在不同近邻下的对比，如图2所示。根据图2，得到各种相似算法的RMSE数据，如表7所示。

图2 协同过滤算法和改进后的混合推荐算法对比

从图2和表7可以看出，使用双因子混合相似度simtfcc(u，v)推荐算法，在阈值TD=8时，近邻在20～25之间，预测评分与真实评分的偏离度RMSE的值在0.183 738 389～0.183 561 899间，此值比使用传统相似度simc(u，v)，simp(u，v)，simcc(u，v)相似度算法得到的值要小，说明使用双因子混合相似度算法推荐效果较好。

表7 协同过滤算法和改进后的混合推荐算法结果对比

4 结 语

本文提出一种基于双因子混合相似度算法，该算法需要引入阈值判断数据是否稀疏，用双因子来平衡协同过滤相似度算法和基于读者属性相似度算法的权重，该算法一方面在一定程度上解决了数据稀疏和冷启动问题，提高了推荐精度，但是该算法中的阈值需要阶段性寻优，阈值是否为最优，对计算相似度的结果影响很大；另一方面，在冷启动时，还需要深入挖掘读者属性隐含的信息来判断读者之间的相似度，这需要进一步深入研究。