矿井涌水对大气降水响应的非线性研究

李建林，王树威，王心义，崔延华

(1.河南理工大学 资源环境学院，河南 焦作 454000；2.中原经济区煤层(页岩)气河南省协同创新中心，河南 焦作 454000)

0 引 言

近年来，深部矿井涌水量与地表水、地下水之间的定量关系是水文过程研究的一个难点和热点问题[1]。矿井涌水量是涌入井下巷道内的地表水、裂隙水、采空区水、岩溶水等总水量，是煤矿开发和安全生产的一个重要指标。我国煤矿数量众多，井下水文地质条件及工作环境差异很大，所以矿井涌水量的影响因素多且影响程度各不相同。我国学者针对矿井涌水量的预测从确定性方法(解析法、水均衡法等)逐渐发展到非确定性随机预测(水文地质比拟法、模糊数学模型、灰色系统理论、BP 神经网络等)，研究方法不断更新[2]。但各种方法在实际中预测精度大都不是很理想[3]。涌入矿井巷道内的地表水包括大气降水、河道水和渠道水等；地下水包括其他层位的裂隙水、采空区水、岩溶水等。环境同位素法和系统模型耦合法是研究这三者关系常用的、有效的方法[4-5]。但环境同位素法只能初步量化矿井涌水的来源，对于矿井涌水如何响应地表水、地下水的变化，还不能作出定量的回答；系统模型耦合法由于边界条件等限制因素的影响，加之模型参数众多，普适性较差[6]。

为深入认识水文循环的变化规律，定量分析工具演变是水文学研究发展的重要脉络之一[7]。非线性科学的发展，为研究上述问题带来了新的视角和方法[8-10]。Mann-Kendall 趋势检验法和R/S分析法是时间序列变化趋势分析的有效工具，在水文、气象等领域有着广泛的应用。但Mann-Kendall 趋势检验法在矿井涌水量分析中还没有见到，而R/S分析法不仅可以对时间序列的变化趋势进行判断，而且还可以确定初值对序列影响的持续时间。灰色GM(1，1)预测在降水量、矿井涌水量时间序列预测中都有广泛的应用，但2个自变量的灰色预测——GM(1，2)的应用很少。大气降水和地表水是平顶山煤业股份七矿(以下简称平煤七矿)矿井涌水的直接补给源，因此本文以平煤七矿矿井涌水量为例，利用Mann-Kendall趋势检验法、R/S分析法，对降水量和涌水量序列变化趋势进行分析，并确定各序列的平均循环周期，在此基础上建立GM(1，2)模型，量化矿井水对大气降水变化的响应。

1 研究区及数据来源

1.1 研究区概述

平煤七矿开采煤层为二组煤，其直接充水水源为石炭系L6-L7薄层灰岩含水层，间接充水水源为寒武系厚层灰岩含水层(图1)。由于L7灰岩与下部寒武系灰岩之间的铝土泥岩隔水层厚度仅3～6 m，在岩溶、裂隙或断裂的发育部位，寒武系灰岩含水层地下水可直接补给L7灰岩含水层，从而成为二组煤开采的主要水害威胁。研究区位于李口向斜南西翼南缘，地层总体倾向北西，倾角10°～15°；局部受到断层构造影响，倾角在40°～60°间。寒武系和石炭系灰岩含水层在浅部煤层露头线一带被第四系或新近系覆盖，在南部北渡山和北干渠一带直接裸露。因此，大气降水和地表水直接补给岩溶水系统西南部的寒武灰岩裸露区，或通过第四系和新近系覆盖层渗漏补给寒武灰岩含水层(图2)。

图1 研究区地层柱状图

图2 研究区灰岩地下水补给示意图

1.2 数据来源

2011年1月—2013年12月在北干渠渠底和乌江河河床已采取了河道固化、导水通道地面注浆截流等多项防护措施。据统计，措施实施前后枯水期矿井涌水量减少426.75 m3/h、雨季涌水量降低1 058.72 m3/h。鉴于以上原因，本研究只讨论大气降水对矿井涌水影响。其中大气降水量数据(2003-01—2015-06)由当地气象局提供；矿井涌水量数据(2003-01—2015-06)由平煤七矿地测科组织实测并提供。所有数据均通过95%的置信度均一性检验。

2 研究方法

2.1 Mann-Kendall检验法

该方法是水文学、气象学中对时间序列进行趋势分析的一种方法。介绍此种检验方法的相关文献很多[11-12]，在此不再作阐述。

2.2 R/S分析法

该方法是针对时间序列的非线性预测方法[13]。对于一个非随机过程，首先须满足

R(n)/S(n)=(an)H，

(1)

式中：R(n)/S(n)为重标极差；n为增量区间长度；a为常数；H为Hurst指数。

对式(1)两边同时取对数，利用最小二乘法进行线性拟合，可得到Hurst指数H(00.5时，表示序列未来的变化趋势与过去一致，即序列具有正持续性，H越大正持续性越强。

为确定时间序列的平均循环周期，引入统计量V(n)，

(2)

V(n)与Hurst指数H的取值范围相对应。当H=0.5时，V(n)-lnn曲线相对比较平缓；当H介于0和0.5之间时，V(n)-lnn曲线向下倾斜；当H介于0.5和1之间时，V(n)-lnn曲线向上倾斜。所以，当V(n)-lgn曲线上出现明显的转折时，所对应的时间长度n为初值对序列影响的持续时间，即序列的平均循环周期T=n[14]。

2.3 GM(1，2)预测模型

2.3.1 数据检验与处理

λ(k)=x(0)(k-1)/x(0)(k)。

(3)

如果所有的级比都落在可容覆盖区间(e-2/(n+1)，e2/(n+1))内，则由以上两序列可以建立GM(1，2)预测模型。否则，须进行平移变换，即取恰当的c，使新生数据列

y(0)(k)=x(0)(k)+c

(4)

满足所有的级比都落在可容覆盖区间(e-2/(n+1)，e2/(n+1))内，方可进行建模。

2.3.2 GM(1，2)模型建立

GM(1，2)表示一阶且含有2个变量的微分方程[13]，相应的微分模型为

(5)

式中a，b为参数。

式中,

通过微分模型的求解，得到预测值

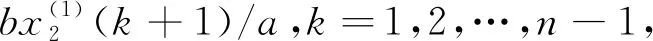
(7)

从而得到相应的原始数据预测值

k=1，2，…，n-1。

(8)

2.3.3 模型的残差检验

灰色预测模型的残差检验是对实测值和预测值之间的误差进行的一种逐点检验的方法[15-16]，通过各点的相对残差值，可以计算出预测模型的精度值P,

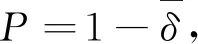
(9)

式中平均相对误差

若P≥0.8，模型通过残差检验；若P< 0.8，则须先修正模型使之满足对精度的要求，才可以进行预测；精度越高，模型拟合得越好。

3结果与讨论

3.1 降水量与涌水量的年际变化特征

以2003年1月—2014年12月共计144个月的降水量和矿井涌水量序列为基础数据，采用Mann-Kendall检验法分析降水量和矿井涌水量年际变化规律(图3)。

由图3(a)可以看出：(1)UF和UB两条曲线均超过显著性水平0.05临界线，说明降水量变化趋势显著；(2)在0.05显著性水平下，UF和UB两条曲线相交于2004年4月，说明从2004年4月开始降水量有明显减少的趋势；(3)在2003—2014年这12年时间里，有很长的一段时间序列UF值小于0，说明降水量总体呈现减少的趋势。

图3 时间序列的Mann-Kendall趋势测试

由图3(b)可以看出：(1)UF和UB两条曲线均超过显著性水平0.01临界线，说明矿井涌水量变化趋势显著；(2)在0.01显著性水平下，UF曲线于2007年3月首次超出临界线范围，以此确定2007年3月是矿井涌水量突变开始的年(月)份，从2007年3月开始矿井涌水量开始有明显的减少趋势；(3)在2003—2014年这12年里，有很长的一段时间序列UF值小于0，说明矿井涌水量总体呈现减少的趋势。

3.2 降水量与涌水量的R/S分析

3.2.1 降水量与涌水量的Hurst指数及其含义

以2003年1月—2014年12月共计144个月的降水量和矿井涌水量序列为基础数据，采用R/S分析法(式(1))分析降水量和矿井涌水量变化趋势(图4)。

由图4(a)可以看出：(1)降水量序列的Hurst 指数H为0.367 7<0.5，所以降水量序列具有反持续性；(2)由于0367 7更接近0.5，而不是0，所以降水量序列具有一定的震荡性。

由图4(b)可以看出：(1)涌水量序列的Hurst 指数H为0.897 3>0.5，所以降水量时间序列具有正持续性；(2)由于0.897 3接近1，持续性更加强烈。

3.2.2 降水量与涌水量序列变化的持续性分析

对降水量与涌水量序列分布做Vn-lnn分析,图5所示。

由图5(a)可以看出：曲线的第一个转折出现在第3个点处，其对应的时间为5个月，即降水量序列的平均循环周期为5个月；由图5(b)可以看出：曲线的第一个转折出现在第18个点处，其对应的时间为20个月，即涌水量序列的平均循环周期为20个月。

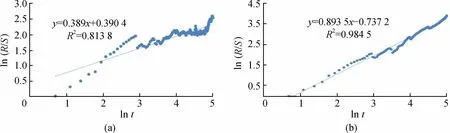
图4 时间序列的R/S分析图

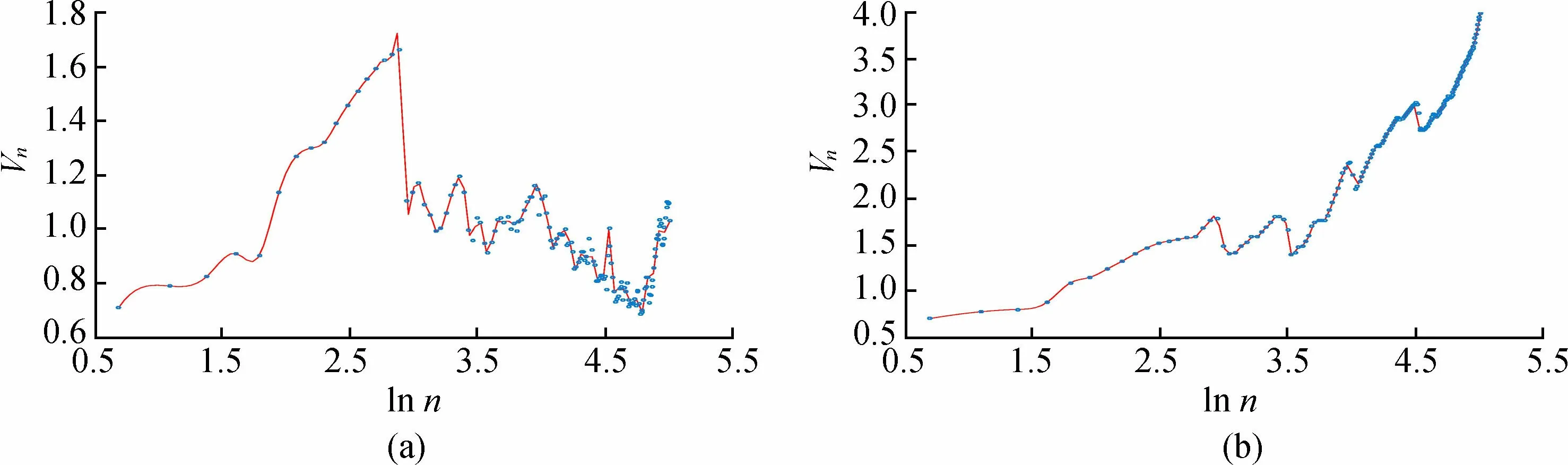
图5 时间序列Vn-ln n曲线

3.3 涌水量对降水量变化的响应

大气降水是矿井涌水量的重要补给源，所以将降水量作为主要影响因子，建立涌水量的GM(1，2)预测模型，以量化降水对矿井涌水的影响。

3.3.1 降水滞后时间的确定

寒武系中统张夏组和上统崮山组，构成煤系基底。对129个钻孔统计，研究区寒武系灰岩揭露厚度0.10～174.87 m，渗透系数0.00 062～24.00 m/d。新近系泥灰岩含水层超覆于寒武系中、上统至山西组地层之上，岩性主要为泥灰岩，局部为角砾岩。据69个钻孔统计结果，研究区新近系泥灰岩厚0.38～22.81 m，渗透系数o 4.0～176.0 m/d。考虑断层的影响，取寒武系地层垂直深度575 m，倾角15°～30°，渗透系数24.00 m/d。通过以上数据对地层进行概化处理后，计算得到大气降水沿出露灰岩岩层流至二煤层下部时间,为46～89 d。

3.3.2 GM(1，2)涌水量预测模型

(1)模型的建立。灰色模型在时间序列样本多、数值标准差大时，预测效果会降低。为提高预测精度，须减少样本数量。由R/S分析得到：涌水量序列的平均循环周期T=20个月，所以选择连续19个月的涌水量作为建模的初值，以预测第20个月的涌水量。

(9)

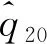
重复以上步骤，可预测2015年3—6月的涌水量。需要注意的是：建模和预测过程一定要进行残差检验，若P>80%则可继续预测(验证过程采用式(9)～(10)计算)，否则终止预测；每次预测时，须保证初始值为19个。

(3)预测结果。按照以上步骤，预测2015年上半年的矿井涌水量(表1)。

由表1可知，滞后两月的涌水量GM(1，2)预测模型结果精度达到了94.25%，预测效果很好。

3.4 讨论

3.4.1 降水量滞后期

降水通过岩层到达煤层底部的时间为46～89 d，即降水量对矿井涌水量的影响大约会滞后1.5～3个月。那么在建立GM(1，2)预测模型时，如何处理降水量与矿井涌水量的对应关系会直接影响到模型的精度。为此，分别假设降水量滞后期为1个月和3个月，建模方法与3.3.2方法一致，与之前按照降水量滞后期为2个月的预测模型进行比较(表2)。

由表2可以看出：降水量滞后期为3个月时，预测模型的精度最低，为90.44%,而降水量滞后期为1个月和2个月时，预测模型的精度基本相当，说明虽然降水量到达煤层底部的时间为46～89 d，但大部分的降水会在2个月内到达。降水量滞后期按2个月建模时，预测模型精度最高，说明对降水量滞后期取平均值是合理的。

表1 GM(1，2)预测2015年上半年涌水量结果

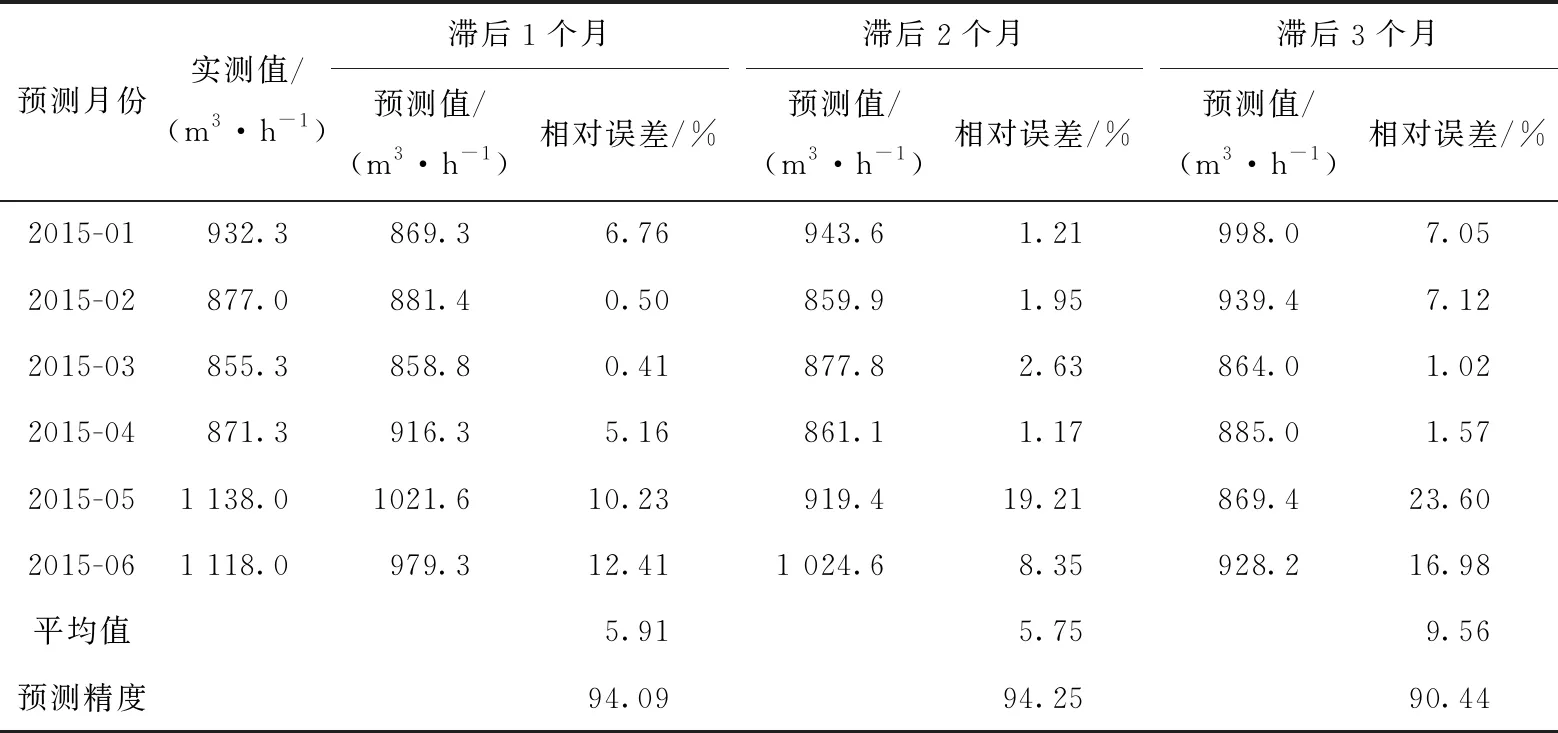
表2 不同降水滞后期涌水量预测模型精度对比

3.4.2 模型的适用性

本研究利用Mann-Kendall检验法、R/S分析法对降水量和涌水量序列变化趋势进行了分析。由于这两种方法的目的是对时间序列的趋势进行大致的判断，属于定性分析；在此基础上建立的R/S-GM(1，2)预测模型属于定量分析。GM(1，2)模型的特点是选择一个与涌水量关系密切的影响因素作为相关因子，建立涌水量的预测模型。由于引入了与矿井涌水量密切相关的因素(观测孔水位、水温、大气降水等)参与预测，可以提高模型的预测精度。陈江峰等[17]、李建林等[18]选择观测孔水位降深作为相关因子，建立了涌水量的GM(1，2)预测模型，预测效果较好。

4 结 论

(1)平煤七矿大气降水量和矿井涌水量分别从2004年4月和2007年3月开始有明显减少的趋势；降水量Hurst 指数为0.367 7，降水量序列具有反持续性，其平均循环周期为5个月；涌水量Hurst 指数为0.897 3，涌水量序列具有正持续性，其平均循环周期为20个月。

(2)平煤七矿降水量对矿井涌水量的影响会滞后1.5～3个月，以此为基础建立了矿井涌水量的R/S-GM(1，2)预测模型，其中以涌水量滞后2个月模型精度最高(达到了94.25%)。该模型以影响涌水量的主要因素——降雨量为模型的相关因子，减少了建模的样本数量，提高了模型的预测精度。