2020年高考“概率统计”经典问题聚焦

■江苏省扬州宝应中学 王志民

2020年高考对概率统计的考查主要围绕“抽样、频率分布直方图、样本的数字特征、独立性检验、古典概型、随机变量的分布列和期望的计算”等核心考点展开，重在考查同学们应用概率统计知识解决实际问题的能力。

聚焦1——样本的数字特征

例 1（2020年高考全国Ⅲ卷文）设一组样本数据x1，x2，…，xn的方差为0.01，则数据10x1，10x2，…，10xn的方差为（ ）。

A.0.01 B.0.1 C.1 D.10

解析：因为数据axi（i=1，2，…，n）的方差是数据xi（i=1，2，…，n）的方差的a2倍，所以所求数据的方差为102×0.01=1。故选C。

素养：平均数、中位数、众数描述其集中趋势，方差和标准差描述其波动大小。当平均数相同时，再考查方差进行决策。

聚集2——用频率分布直方图的数据估计总体

例 2（2020年高考天津卷）从一批零件中抽取80个，测量其直径（单位：mm），将所得数据分为9组：[5.31，5.33），[5.33，5.35），…，[5.45，5.47），[5.47，5.49]，并整理得到图1所示的频率分布直方图，则在被抽取的零件中，直径落在区间[5.43，5.47）内的个数为（ ）。

图1

A.10 B.18 C.20 D.36

解析：根据直方图，直径落在区间[5.43，5.47）内的频率为（6.25+5.00）×0.02=0.225，则直径落在区间[5.43，5.47）内的零件个数为80×0.225=18。故选B。

素养：在频率分布直方图中，每一个小矩形的面积就是相应的频率或概率，所有小矩形的面积之和为1，利用频率分布直方图估计总体的分布情况：（1）最高的小长方形底边中点的横坐标即是众数；（2）中位数左边和右边的小长方形的面积和是相等的；（3）平均数等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和。

聚焦3——古典概型

例 3（2020年高考全国Ⅰ卷文）设O为正方形ABCD的中心，在O，A，B，C，D中任取3点，则取到的3点共线的概率为（ ）。

解析：如图2，从O，A，B，C，D中任取3个点，有{O，A，B}，{O，A，C}，{O，A，D}，{O，B，C}，{O，B，D}，{O，C，D}，{A，B，C}，{A，B，D}，{A，C，D}，{B，C，D}，共10种不同取法，3点共线只有{A，O，C}与{B，O，D}，共2种情况，由古典概型的概率计算公式知，取到3点共线的概率为故选A。

素养：古典概型中基本事件数的探求方法：（1）列举法。（2）树状图法：适合于较为复杂的问题中的基本事件的探求。（3）列表法：适用于多元素基本事件的求解问题，通过列表把复杂的题目简单化、抽象的题目具体化。（4）排列组合法：适用于限制条件较多且元素数目较多的题目。

聚焦4——构建二项分布模型

例 4（2020年高考北京卷）某校为举办甲、乙两项不同活动，分别设计了相应的活动方案：方案一、方案二。为了解该校学生对活动方案是否支持，对学生进行简单随机抽样，获得数据如表1：

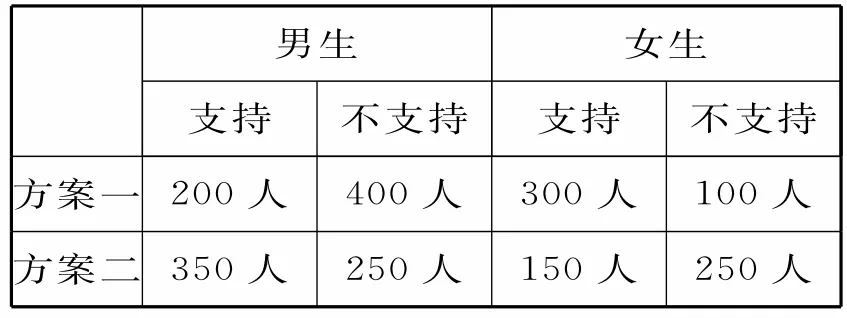
表1

假设所有学生对活动方案是否支持相互独立。

（1）分别估计该校男生支持方案一的概率，该校女生支持方案一的概率；

（2）从该校全体男生中随机抽取2人，全体女生中随机抽取1人，估计这3人中恰有2人支持方案一的概率；

（3）将该校学生支持方案二的概率估计值记为p0，假设该校一年级有500名男生和300名女生，除一年级外其他年级学生支持方案二的概率估计值记为p1。试比较p0与p1的大小。（结论不要求证明）

解析：（1）该校男生支持方案一的概率为该校女生支持方案一的概率为。

（2）这3人中恰有2人支持方案一有以下两种情况：①一名男生和一名女生支持方案一，一名男生支持方案二，概率为×两名男生支持方案一，一名女生支持方案二，概率为所以这3人中恰有2人支持方案一的概率是。

（3）p1＜p0。

理由：估计该校男生、女生人数的整体比例为600:400=3:2，男生对方案二的支持率高于女生。而一年级男生、女生人数的比例为500:300=5:3，高于整体比值，一年级对方案二的支持率高于平均值，所以除一年级外其他年级学生支持方案二的概率估计值p1小于该校学生支持方案二的概率估计值p0。

素养：有关随机变量的分布列与数学期望问题，互斥事件和相互独立事件的概率计算公式等是基础，有时合理构建独立重复试验，利用二项分布模型可简化计算概率。

聚焦5——期望方差

例 5（2020年高考全国Ⅲ卷理）在一组样本数据中，1，2，3，4出现的频率分别为p1，p2，p3，p4，且则下面四种情形中，对应样本的标准差最大的一组是（ ）。

A.p1=p4=0.1，p2=p3=0.4

B.p1=p4=0.4，p2=p3=0.1

C.p1=p4=0.2，p2=p3=0.3

D.p1=p4=0.3，p2=p3=0.2

解析：借助期望和方差的意义对选择支逐一验证，对于A选项，该组数据的平均数为=（1+4）×0.1+（2+3）×0.4=2.5，方差为=（1-2.5）2×0.1+（2-2.5）2×0.4+（3-2.5）2×0.4+（4-2.5）2×0.1=0.65；

因此，B选项这一组标准差最大。故选B。

素养：E（X）=x1p1+x2p2+…+xnpn，D（X）=[x1-E（X）]2·p1+[x2-E（X）]2·p2+…+[xn-E（X）]2·pn，当随机变量含参数或某一个概率为参数时，可构建期望或方差是关于某参数的二次函数，从而研究参数的变化趋势。