卷积神经网络模型剪枝结合张量分解压缩方法

巩凯强，张春梅，曾光华

（北方民族大学计算机科学与工程学院，银川 750021）

（∗通信作者电子邮箱kq192011@sina.com）

0 引言

近年来，卷积神经网络（Convolution Neural Network，CNN）为代表的神经网络在计算机视觉、自然语言处理等领域取得了突破性的进展。然而，随着神经网络的识别精度不断提升，网络结构也越复杂，需要占用更多的计算和存储资源，“深度结构”带来高效性的同时，也增大了模型的参数量。卷积网络模型的复杂度主要体现在两个方面：一是卷积层包含了网络90%的运算量；二是卷积层产生的庞大参数量，解决这两个问题，具有重要的应用理论意义。现阶段的神经网络模型训练主要在服务器和图形处理器（Graphics Processing Unit，GPU）端，对于一些应用场景已经不能满足实际的需求，如在自动驾驶、知识推理的落地，当前阻碍神经网络落地的原因主要是庞大的参数量难以在嵌入式端等资源受限的设备上部署，因此，模型压缩以降低模型中冗余参数为目标，将有利于神经网络在嵌入式端的落地。

本文的主要工作如下：

1）研究了卷积神经网络的剪枝方法。以Lenet5 和更快的区域卷积神经网络（Faster Region with Convolutional Neural Network，Faster RCNN）为剪枝对象，分析不同均值和方差的滤波器提取的图像特征，得出本文衡量卷积核参数重要性的评价标准，以此标准对卷积网络进行剪枝。

2）研究了网络模型加速方法。以Faster RCNN 为压缩对象，将本文的剪枝评价标准结合张量分解的方法，在稀疏度较高的卷积核分解，并选择一组最优秩作为张量分解的重构误差值对Faster RCNN 进行混合压缩，压缩后测试模型在树莓派4B上的加速效果。

1 相关工作

剪枝以神经网络的冗余参数剪除为目标，反向传播（Back Propagation，BP）神经网络［1］流行之后，对神经网络的剪枝相应地发展起来［2］。Mozer 等［3］提出Skeletonization 算法对神经网络剪枝；LeCun 等［4］提出了OBD（Optimal Brain Damage），使用二阶梯度衡量网络模型参数的重要性，从而去除冗余参数。当卷积神经网络发展起来后，Jaderberg 等［5］使用低秩分解方法对卷积神经网络进行分解，实现了4.5 倍的加速效果而准确度误差在1%内；Zhang 等［6］采用多次“剪枝-重训练”的方式对AlexNet 进行网络剪枝；Liu 等［7］采用稀疏结构对卷积网络压缩；Han 等［8］使用L1 范数和L2 范数作为模型参数的重要性评价；Lebedev 等［9］使用最小绝对值收敛和选择算子（Least absolute shrinkage and selection operator，Lasso）对参数约束以产生稀疏性；Yuan 等［10］使用分组变量回归对权值参数约束；Molchanov等［11］基于泰勒展开提出使用一阶导数与权重的乘积绝对值作为参数重要性评价进行渐进式剪枝；Li等［12］提出量级裁剪方式，使用权重的绝对值和大小作为衡量参数重要性的评价方式进行多次剪枝；He 等［13］对通道剪枝（Channel Pruning）进行改进，使用强化学习得到各层剪枝率的最优组合，然后对卷积核进行剪枝。

一个深度卷积网络模型中，高层卷积层维度较大，其权值稀疏度较高，压缩的直接方法是低秩表示原张量，低秩分解是通过减少卷积核参数达到压缩模型的效果，其思想就是使用因子分解将一个张量用几个参数较少的张量来近似表示。低秩分解按照对卷积核的分解维度的不同主要有两种：空间维度的分解和通道维度的分解，前者将3×3的卷积核分解为3×1或者1×3；后者将输入和输出通道的维度分解（如512×512 分解为300×300）。Denton 等［14］用低秩分解的ZFNet网络的卷积层进行加速，实现2.5倍的实际加速同时准确率下降在1%以内。Lebedev等［15］提出了简单二步法加速卷积层：第一步，使用非线性最小二乘法来计算CP（Canonical Polyadic）分解，将卷积核张量分解为秩为1的张量形式；第二步，使用CP分解将具有小卷积核的四个卷积层替换原来的卷积层。Tai等［16］提出了一种计算低秩张量分解的新算法，用于去除卷积核中的冗余。

以往的剪枝算法，以权值大小来衡量卷积核的贡献度，这容易裁剪重要的权值，如在人脸关键点检测时，整张人脸的很多特征：眼睛的边缘和颜色特征，即使权值很小但它提取的特征有利于分类与回归。本文基于上述研究，从图像滤波器的角度出发，剪除每层冗余滤波器来减少模型中的冗余参数和计算量；同时探索剪枝结合张量分解对卷积神经网络压缩。

2 理论分析

在一个确定结构的深度卷积网络模型中，大量的参数能够提升网络模型的分类能力，但同时也容易使网络模型过拟合，反之过少的参数使网络模型欠拟合，可见有效的压缩参数量方法对网络模型性能的重要性。

2.1 剪枝标准

在传统的图像处理方法中，通过人工设定卷积核参数进行卷积运算来获得图像的特征表示，提取特征方式通过卷积操作如式（1）：

如图1（卷积核不同权值参数提取的图像特征）可得出：Prewitt 算子（图1（b））和Laplace 算子（图1（c））可以获得图像的边缘特征，CNN 学习到的卷积核存在与Prewitt 算子和Laplace 算子相似的特征提取作用；若对图像进行均值滤波器（图1（d））卷积操作，可以看出提取到图像的基本轮廓信息，同样CNN 中存在很多权值相近均值滤波器，这说明图像集中在低频和高频特征可以用不同权值参数的滤波器提取，通过激活函数对提取的特征进行非线性变换，多个滤波器提取的非线性变换的向量最后组合成一幅图像整体特征。

图1 卷积核不同权值参数提取的图像特征Fig.1 Image features extracted by different weight parameters of convolution kernel

基于上述分析，均值较大的卷积核提取到低频信号，而方差较大的卷积核锐化图像，提取到高频信号，方差较大的提取算子更能提取出图像的边缘特征。而边缘是构成图像的最基本的特征，卷积核边缘提取的效果直接影响图像识别和理解。滤波器裁剪的模型压缩即在裁剪过程中，最大限度地保留能够提取到图像轮廓信息和边缘信息的滤波器，因此，本文认为卷积网络中均值和方差较小的滤波器为冗余滤波器，采用聚类的方式将均值和方差较小的滤波器分离出进行裁剪。以训练好的Faster RCNN 模型为例，该主干网络中共有13 层卷积层：Conv1_1、Conv1_2、Conv2_1、Conv2_2、Conv3_1、Conv3_2、Conv3_3、Conv4_1、Conv4_2、Conv4_3、Conv5_1、Conv5_2、Conv5_3，以及在区域推荐网络（Region Proposal Network，RPN）中的RPN_Conv、RPN_Cls 卷积层，分别计算每个卷积核参数的均值m 和方差s，设定卷积核C 形状为（h，w，n，t），其均值和方差如式（2）和式（3）：

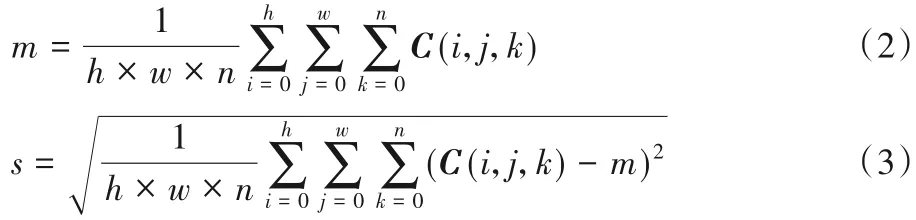
Conv3_1层卷积核均值直方图如图2所示，方差直方图如图 3 所示，则 Conv3_1 层卷积核均值范围为-0.000 5～-0.002，Conv3_1层卷积核方差范围为0.015～0.025，该区间内的滤波器离散度相似，对其他层的卷积层参数提取后分布情况与之类似。

依据卷积核权值分布特征，通过距离相似性度量关系对均值和方差具有相似性的滤波器聚类，则Conv3_1 层卷积核统计量特征分类如图4所示。

卷积核的贡献度评估分类展出了卷积核参数的3 个特点：1）每层卷积核参数的均值和方差分布在不同区间，有些卷积核的均值很低，说明该卷积核学习的权值参数提取到图像中的低频信号部分或者背景部分，即存在冗余性参数；2）卷积核参数类似正态分布，可以将每个卷积核的贡献度按照相似性函数分为两大类；3）均值较低和方差较大的卷积核说明其学习的权值参数波动大，提取到图像的灰度值等变化幅度较大的高频信号，该类卷积核的贡献度较大，因此剪枝过程中考虑方差评价标准对卷积核的贡献度度量也是较为重要。

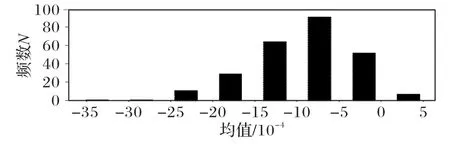
图2 Conv3_1层均值直方图Fig.2 Mean histogram of Conv3_1 layer

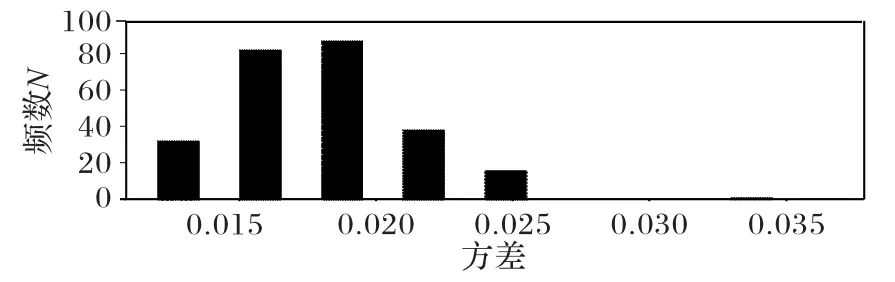
图3 Conv3_1层方差直方图Fig.3 Variance histogram of Conv3_1 layer

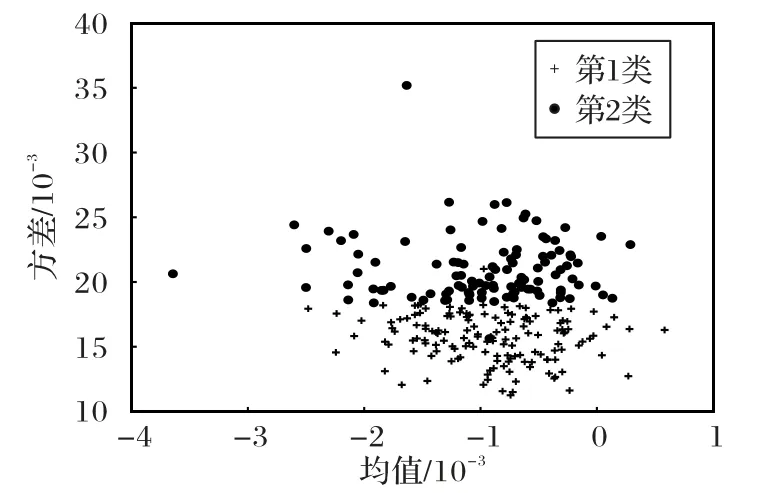
图4 卷积核统计量特征的贡献度评估分类Fig.4 Contribution evaluation classification of convolution kernel statistics features

2.2 卷积核张量低秩表示

由于卷积神经网络规模逐渐向更深、更大层次发展，一般而言，网络性能正相关于网络深度和参数量，但过深的网络和过多的参数会带过拟合、梯度消失现象。一种改进现有网络结构的手段是将卷积层等密集连接结构转化为稀疏的连接形式，因为这可以降低计算冗余度，同时维持网络的表达能力，其数学依据是一个大型稀疏矩阵分解为小的密集子矩阵，以此来近似稀疏结构，张量分解对于去除冗余信息和加速卷积计算是一种极为有效的方法，本文对深层次的卷积网络模型，剪枝结合张量分解进行模型压缩。向量称为一维张量，矩阵称为二维张量，以一个二维张量表示的图像为例，低秩表示后重构图像信息如图5（奇异值数对图像压缩的失真对比）可得出：一张300×200 大小的图像，奇异值Rank 分别设定为（20，40，150），Rank=40（图5（c））前40 个奇异值就能大致还原图像，这是因为在奇异值矩阵中奇异值减小得特别快，可以用最大的奇异值和对应的左右奇异向量来近似描述矩阵，因此对具有稀疏性的矩阵或者张量用其低秩近似表示可以有效压缩参数量。

卷积神经网络中的卷积核为四维张量，表示为W ∈Rd×d×I×O，其中d、I、O分别表示卷积核的尺寸、输入通道和输出通道。常见的张量分解方法有CP分解和Tucker分解，Tucker 分解可将卷积核分解为一个核心张量与若干因子矩阵，是一种高阶张量的主成分分析方法，设分解的秩（r1，r2，r3，r4），其表达形式如式（4）：

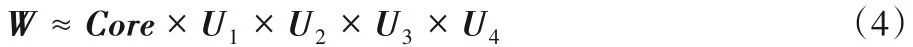
图5 奇异值数对图像压缩的失真对比Fig.5 Distortion comparison of singular value number to image compression

图6 展示了将一个张量W ∈Rd×d×I×O，分解为和W'∈Rr4×d×d×I过程，W（图6（a））为原始张量，参数量q=d2IO；P和W（'图6（b））为分解后张量，此时参数量对于大多数网络Or4远远小于，并且秩越小，压缩效果则越明显。

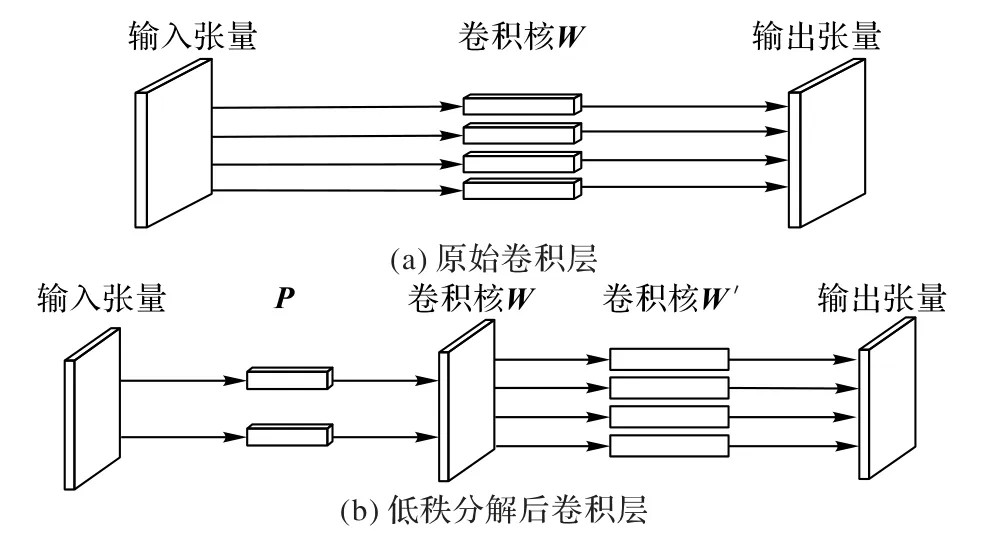
图6 张量分解过程示意图Fig.6 Schematic diagram of tensor decomposition process

3 方法描述

本章详细描述均值方差剪枝结合张量分解的混合压缩方法，压缩方法流程如图7 所示，主要包括剪枝流程和张量分解的低秩表示，剪枝方法剪除相对不重要的权值参数使得参数量减少，而张量分解将具有稀疏性的张量低秩表示，通常深层次的卷积神经网络，单独的剪枝方法会带来较大的精度损失，在网络微调时需增加迭代次数使模型收敛，带来重训练时间长的问题，若在稀疏性较大的高维度卷积层低秩分解，就避免了剪枝方法剪除重要的权值带来的精度损失，同时产生的不同尺寸稀疏级联卷积层可以加速压缩后的网络模型收敛。

3.1 网络模型剪枝方法

一个卷积核的均值和方差越小的条件下，说明该卷积核学习到背景信息或者低频冗余信号，在保证网络精度的前提下裁剪这些贡献度较小的卷积核。

网络训练是优化卷积核参数W 的过程，来减小定义的损失函数E(T|f，W)，T 为训练集，网络裁剪时优化参数子集Wp，其中贡献度较大的卷积核Wp∈W，优化裁剪的精度损失如式（5），剪枝流程如图8所示。

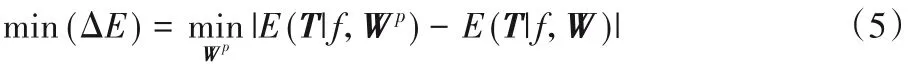
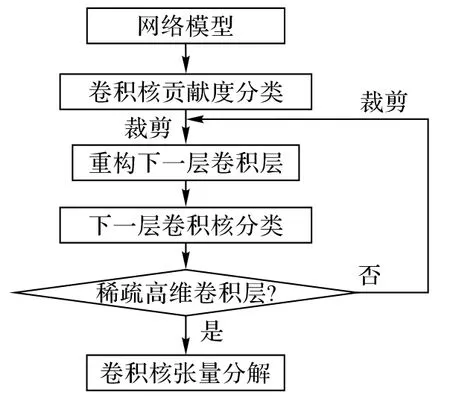
图7 剪枝结合张量分解的混合压缩流程Fig.7 Flowchart of mixed compression of pruning and tensor decomposition

基于均值和方差的卷积核裁剪过程，其卷积层的具体剪枝流程如算法1所示。

算法1 剪枝算法。

输入 训练好的网络模型，开始剪枝的卷积层，聚类终止阈值threshold。

输出 压缩后的网络模型。

第1步 根据2.1节剪枝标准计算卷积层W的每个卷积核均值和方差，组成聚类数据样本dataset｛（m（1），s（1）），（m（2），s（2）），…，（m（n），s（n））｝，其中m（1），m（2），…，m（n）＞T0。

第2步 优化值E ≥threshold时

1）初始2 个聚类中心Zj(O)，计算dataset 中的每个点与质心的距离Di，j，并划分到距离较近的质心（C1、C2）所属集合；

2）重新计算每个集合的质心qi；

4）如果E ＜threshold，返回C1和C2的索引值Index0 和Index1。

第3 步 比较C1和C2两类卷积核均值的绝对值和即|S1|、|S2|，保留较大的一类卷积核。

第4 步 在较小的一类卷积核中找出方差大于阈值T1，则该滤波器保留。

第5 步 上一层剪枝后，重构下一层卷积核的连接通道，继续用上述剪枝步骤，直到完成所有需剪枝的卷积层。

第6 步 对深度卷积网络剪枝后进行微调。剪枝完成后，加载剪枝前训练好的参数继续训练使网络重新收敛。

第7步 输出剪枝的网络。

算法实现中，从裁剪的第一层卷积层开始，独立地裁剪每一层滤波器。裁剪时本文没有采用根据均值或方差阈值大小直接对模型进行裁剪，因为若在某一层滤波器的均值或方差值均小于阈值，则该层所有滤波器均会被裁剪而对模型产生结构性破坏，本文依据模型中各层卷积层滤波器学习到的数据固有属性，通过聚类的方法对滤波器分类，这样做的好处是剪枝中自动找出均值和方差的剪枝阈值，尽可能地将较小均值和方差冗余滤波器提取到图像重要特征的滤波器分为几个不同簇，之后保留冗余滤波器中方差大于T1的滤波器，该方法适用于卷积核均值和方差连续分布在不同区间，采用类聚方式找出冗余滤波器的分布区间从而裁剪。

图8 卷积核裁剪流程Fig.8 Pruning process of convolution kernel

3.2 张量分解算法实现

数学上一个矩阵的奇异值分解是唯一的，从而可以将一个矩阵运算稀疏化，而一个四阶张量分解是一个非确定性多项式（Nondeterministic Polynomially，NP）问题，分解结果存在多样性，目前可行的分解方法为高阶正交迭代算法。对于3×3 或者5×5 大小的卷积核，其分解因子矩阵为单位阵，假设待分解张量W(h，w，s，t)，卷积核分解的正交迭代步骤如下：

1）确定压缩张量输入和输出通道方向的压缩秩（r3，r4）。

2）分解输入和输出通道方向的因子矩阵A1、A2，其中A1∈Rs×r3，初始化W(1)为展开的前r3个主奇异值对应的左奇异向量组；A2∈Rr4×t，初始化W(2)为展开的前r4个主奇异值对应的左奇异向量组。

3）求解分解的核心张量g，如式（6）：

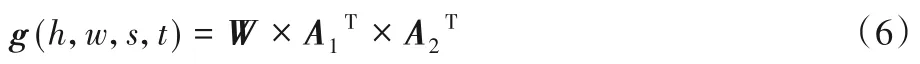
5）得到的核心张量g 及因子矩阵构造相似矩阵Rec(h，w，s，t)，然后计算构造误差如式（7）：

6）重复过程3）～5）步骤，直到构造误差小于阈值10-5。

7）算法返回g(h，w，s，t)，U(1，1，s，r3)，V(1，1，r4，t)，其中g、U、V张量分别作为分解后的第2、1、3个卷积核的权值。

4 实验验证与分析

为了验证上述方法，本文以Lenet5 和VGG16 基础的Faster RCNN 为研究对象，Lenet5 网络进行剪枝，剪枝流程如前文所述。“剪枝+张量分解”对深度卷积网络Faster RCNN 压缩，训练集/测试集采用Pascal VOC 数据集，实验环境：Windows 10 操作系统、8 GB 内存、网络模型训练框架tensorflow和嵌入式系统树莓派4B。

4.1 在Minst数据集的Lenet5剪枝

对Lenet5 中的两层卷积层剪枝，然后测试其准确度在Minst 数据集变化，剪枝前后的卷积核形状和裁剪率如表1所示。

本文中的剪枝方法和主流的剪枝后准确度对比如表2所示。

为了验证本文中均值和方差的剪枝评价标准，剪枝后的Lenet5 和文献［12］的剪枝标准在Minst 数据集上特征图可视化，如图9（不同剪枝标准剪枝后特征）可得出：加入方差剪枝标准（图9（c））的压缩方法，剪枝后更能够准确提取到图像边缘、轮廓等特征。

表1 Lenet5剪枝前后卷积核形状Tab.1 Shape of convolution kernel before and after pruning of Lenet5

表2 所提方法与其他方法的剪枝结果对比 单位：%Tab.2 Pruning result comparison of the proposed method with other pruning methods unit：%

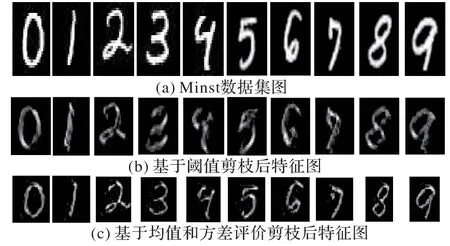
图9 不同剪枝标准剪枝后Minst数据集的特征图Fig.9 Feature map of Minst dataset after pruning with different pruning standards

4.2 深度网络模型的混合压缩

Faster RCNN 算法是目标检测领域领先的算法之一，该算法框架由2 个部分组成：特征提取网络和区域生成网络，本节对VGG16 为基础的特征提取网络和区域生成网络的卷积层剪枝结合张量分解压缩，来验证这种方法的压缩效果。Conv4层前网络的卷积层输出维度较低，输出通道的稀疏性较低，因此采用2.1 节剪枝标准剪除冗余滤波器；而在维度较高的Conv5 层的输入输出通道均为512，其权值分布如图10 所示，纵坐标表示在不同迭代次数下权值大小，权值参数范围为-0.01～0.01，如此稀疏的数据分布适合低秩压缩。

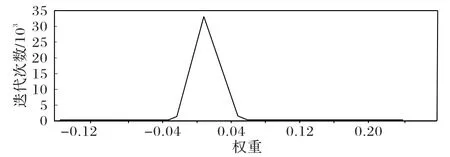
图10 Faster RCNN中Conv5_1权值分布Fig.10 Weight distribution of Conv5_1 in Faster RCNN

在tensorboard 中可视化本文的剪枝标准结合张量分解的损失值，并比较相同压缩率下直接用权值阈值方式的损失值，在高维卷积层进行张量分解的剪枝迭代30 000 步收敛于0.6附近，而权值阈值的剪枝方式需要迭代40 000～50 000 步才能达到收敛。这是因为张量分解将稠密的卷积层分解为几个稀疏结构的卷积层，可以降低计算复杂度和参数量，同时将一层变为多层的策略，通过选择一组秩得到较小的重构误差，近似出原卷积核参数，在fine-tune 时可以较快地达到收敛状态，对于更深层次的卷积网络而言，结合张量分解的剪枝可以加快网络收敛，有效缩短了剪枝后的网络重训练时间。

混合压缩后Faster RCNN 卷积核参数量如表3 所示，Conv4_3～Conv5_2 低秩分解时秩设定为（128，128），网络层的参数量为每个维度值之积，计算得出混合压缩后所有卷积层的参数量大小为31.3 MB，网络卷积层参数量达到了54%的压缩率。

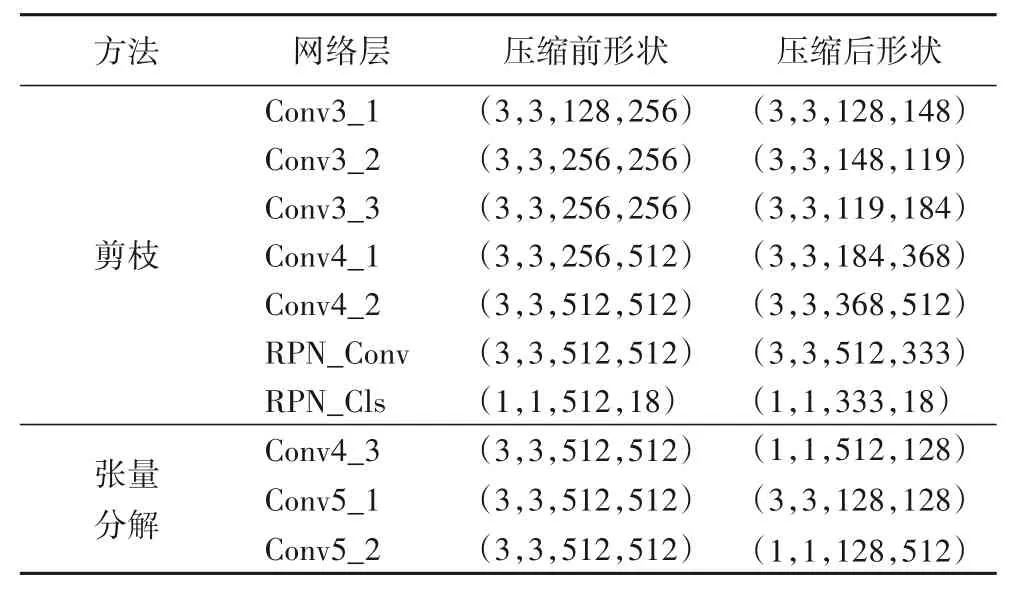
表3 混合压缩后的Faster RCNN卷积核参数量Tab.3 Convolution kernel parameters of Faster RCNN after mixed compression

低秩分解后网络的前向计算加速如表4所示，以Conv5_1层为例，实验结果表明，秩值取（128，128）或者（256，256）基本能重构待分解的张量。

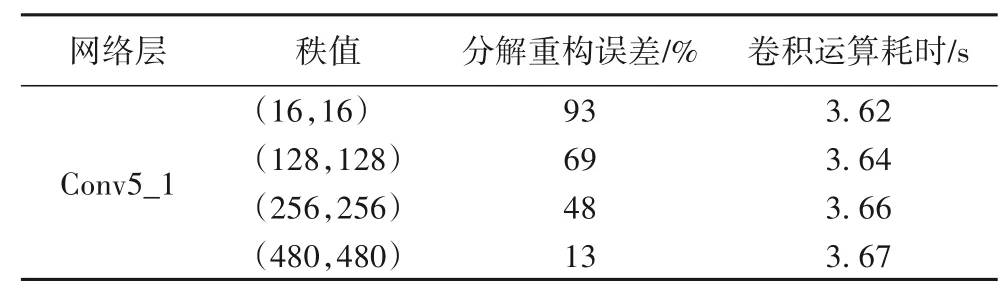
表4 张量分解秩值对卷积层前向计算加速效果Tab.4 Comparison of forward calculation acceleration effect of convolutional layer with tensor decomposition of different rank

压缩前后Faster RCNN 在PASCAL VOC 的P-R（Precision-Recall）曲线以及AP（Average Precision）如图11所示。

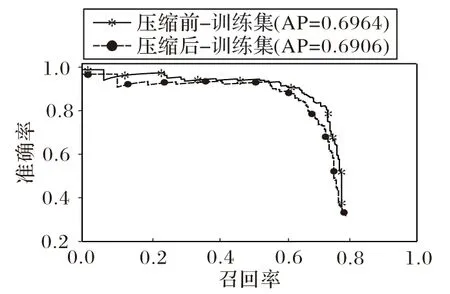
图11 压缩前后Faster RCNN的PR曲线Fig.11 PR curve of Faster RCNN before and after compression

将提出的“均值、方差剪枝+张量分解方法”与其他裁剪算法下的Faster RCNN的AP值进行比较，具体结果如表5所示。

1）基于张量分解的压缩算法［18］：低维卷积层到高维卷积层均用奇异值分解（Singular Value Decomposition，SVD）。

2）随机裁剪（Random Pruning）［19］：对于每一个卷积层，随机裁剪一定量的滤波器来对模型进行压缩和加速。

3）卷积层先基于Lasso 回归进行网络剪枝［20］，再进行SVD。

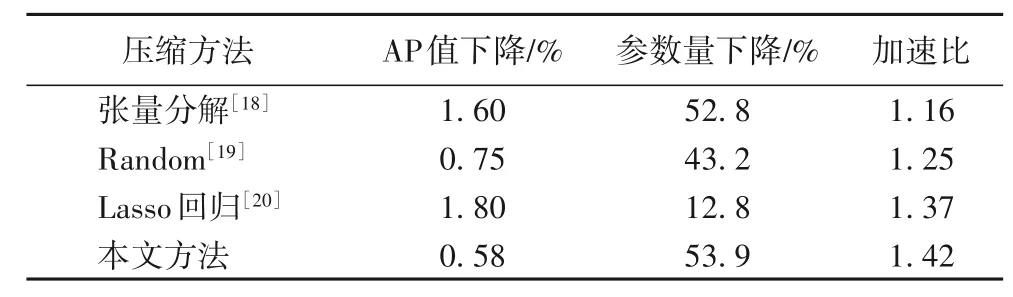
表5 不同压缩方法下的Faster RCNNTab.5 Faster RCNN under different compression methods

在对比实验中，以删除冗余参数作为有效的压缩神经网络手段［21］，对权值具有稀疏性的Faster RCNN 为压缩模型，分别用3 种策略进行对比压缩后的模型效果：文献［18］中所有卷积层进行张量分解，在稀疏度不大的低维卷积核分解误差累积到高维卷积核从而影响精确度；文献［19］随机方式裁剪滤波器，裁剪率越大，贡献度较大的滤波器被裁剪的概率也越大；文献［20］是L1 范数惩罚权值小的方式，剪枝中也会裁剪离散度较大卷积核，采用均值和方差的权值贡献度评价方式能够保留映射边缘、轮廓特征的卷积核，在具有稀疏性的高维度卷积层只需对训练好的模型奇异值分解，达到网络模型加速的目的；本文从不同的角度压缩模型，提出的均值和方差剪枝标准结合张量分解的方法优于其他方法，由于该方法的精确度变化和模型加速取决于分解时的秩，因此需要多组秩值确定压缩模型的最优秩。

5 结语

本文针对深度卷积神经网络拥有巨大的参数量和计算量，研究了基于均值和方差剪枝+张量分解的压缩方法，为了验证算法有效减少参数量和计算量，分别在Lenet5 和Faster RCNN 进行了剪枝，明显降低了模型的存储需求，使得模型在损失精度极少的情况下，运行效率和存储效率同时提升。未来工作是进一步探索表征卷积核参数重要性的量，利用张量稀疏性，找出卷积层最优秩占比算法，使得压缩后模型精确度和加速效果达到最优。