基于后悔理论及EDAS法的概率语言多属性群决策方法

童玉珍，王应明

（福州大学经济与管理学院，福州 350116）

（∗通信作者电子邮箱576856545@qq.com）

0 引言

决策在我们的日常生活中是非常普遍但又极其重要的一项活动。在传统的模糊语言决策方法中，决策者仅通过一个语言术语去表达自己的偏好或者评价，然而在许多复杂的决策问题中，决策者通常很难仅用单一的语言术语来表达自己犹豫不决的定性意见。为了解决这类问题，Rodriguez 等［1］提出了犹豫模糊语言术语集，它在实际的定性决策中，可以用来表示复杂、犹豫的语言表达。需要指出的是，目前大多数关于犹豫模糊语言术语集的研究中，都默认决策者提供的语言术语具有同等的重要性，事实上决策者可能会更倾向于某个评价语言术语，这些语言术语集可能有不同的重要性程度。因此，Pang 等［2］提出了概率语言术语集（Probabilistic Linguistic Term Set，PLTS），在不丢失任何原始语言信息的前提下通过添加概率信息拓展了犹豫模糊语言术语集，概率语言术语集不仅允许决策者在决策过程中出现犹豫不定的情况，同时结合概率来表达决策者的偏好信息。概率语言术语集的提出得到了许多学者关注，Zhang等［3］提出了概率语言的偏好关系及其一致性指数，并提出一种自动优化的方法去提高一致性；Gou 等［4］提出了概率语言新的基本运算法则；Lin 等［5］提出了概率语言术语集的距离度量方法并将其运用于多属性群决策中；Bai 等［6］运用图解法去分析概率语言的结构并提出概率语言术语集的新的比较方法；Liao 等［7］提出了一种利用概率语言信息进行多准则决策的线性规划方法；文献［2，7-10］则将一些经典的决策方法如TOPSIS（Technique for Order Preference by Similarity to Ideal Solution）、ORESTE（Organísation，Rangement Et Synthèse Dedonnées Relarionnelles）、LINMAP（LINear programming technique for Multidimensional Analysis of Preference）、PROMETHEE（Preference Ranking Organization Methods for Enrichment Evaluations）、BP（Bidirectional Projection）等拓展到了具有概率语言信息的多属性决策中。

目前越来越多学者关注到决策者心理行为对于现实决策过程及决策结果的影响。在众多基于有界理性的方法中，运用最广泛的是前景理论［11］和后悔理论［12］。由于后悔理论在计算过程中没有较多的参数，计算简便，越来越多的学者将其运用于多属性决策问题中。Xia［13］考虑了策者的犹豫行为和后悔行为，提出豫模糊语言多准则决策以识别出不同类型的最佳选择；Peng 等［14］结合后悔理论与ELECTRE Ⅲ（ELimination Et Choix Traduisant la REalité）法建立了能够有效支持新能源投资决策的模型；Jiang 等［15］考虑决策者后悔规避的心理行为提出了一种新的模糊广义后悔决策方法；Wang等［16］提出一种新的基于项目的后悔理论方法来解决区间二型模糊环境下的决策问题。Keshavarz 等［17］在2015 年提出了离平均方案（平均解）距离的评价（Evaluation based on Distance from Average Solution，EDAS）方法，它不仅在不同的权重下具有稳定性，而且与现有的一些决策方法如VIKOR（VlseK riterijumska Optimizacija I KOmpromisno Resenje）、AHP（Analytic Hierarchy Process）等有很好的一致性。EDAS 法具备的稳定性、有效性及计算过程的简易性，使其在近几年得到了较快的发展，Kahraman 等［18］结合直觉模糊集提出了直觉模糊EDAS 法；Keshavarz 等［19］考虑一种符合正态分布的决策属性值提出了随机EDAS法；Stanujkic等［20］将EDAS法拓展到了属性值为区间灰色值的多属性决策问题中。

基于以上分析，很多学者针对属性值为概率语言的决策问题，提出了一些决策方法，但需要指出的是大多数的决策方法假设决策者是一个“完全理性人”。但在不确定的前提之下进行决策时，对于决策者的非理性行为因素应予以着重考虑，这也更加符合决策的实际情况；而关于后悔理论的多属性决策问题的研究及探讨，大多数是基于决策属性值为犹豫模糊数、区间值或精确值等，而对于决策属性值为概率语言的研究目前还较少。而在时间紧迫、信息不完全以及在决策者自身认知的局限性的情况下，决策者很难及时地对决策属性值给出精确的评价值，而是会更加倾向于运用更符合人类思维习惯的语言术语去给出科学的符合现实的评价值。最后，EDAS作为近几年提出的较新的多准则决策方法，一般运用于属性值为数值的决策问题中，而对于属性值为定性的特别是运用于属性值为概率语言的多属性决策问题的相关研究还较少。

针对现有研究的分析，本文考虑将后悔理论及EDAS 法拓展到概率语言信息的决策环境下：首先利用新的概率语言熵及交叉熵建立属性权重确定模型；然后考虑决策者后悔规避的心理行为同时将群体满意度公式拓展到概率语言信息下用于计算后悔、欣喜感知效用值；最后针对属性值为概率语言术语集决策问题，结合EDAS 法与后悔理论，提出一种基于后悔理论及EDAS 法的概率语言多属性群决策方法，并将其运用于突发事件的处理与决策中。

1 基本概念

1.1 概率语言术语集

定义1基于加性语言评价量表S={sα|α=-τ，…，-1，0，1，…，τ}（其中τ 是一个正整数），根据文献［2］概率语言术语集被定义为：

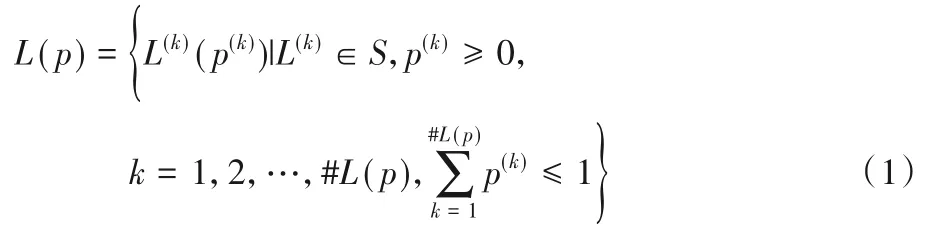
其中：L(k)(p(k))是具有概率信息为p(k)的语言术L(k)；r(k)是语言术语集L(k)的下标；#L(p)是L(p)中语言术语的数量。

根据文献［21］中提出的犹豫模糊语言熵及交叉熵、文献［4］提出的概率语言等价变换函数，并结合概率语言性质及与犹豫模糊语言的关系，本文提出概率语言熵及交叉熵的相关定义。

定义2令S={sα|α=-τ，…，-1，0，1，…，τ}为语言评价量表，L(p)为概率语言术语集，其中L(k)(p(k))是一个具有概率信息为p(k)的语言术语L(k)，#L(p)是L(p)中语言术语的数量，且#L(p)=K，则L(p)的熵需要满足以下条件：

1）0 ≤E(L(p)) ≤1；

2）当g(L(p))=0 或g(L(p))=1 时，若 有p(k)=1，E(L(p))=0；

3）当 且 仅 当#L(p)=2，p(1)=p(2)=12 且g(L(1))+g(L(2))=1时，E(L(p))=1。

基于犹豫模糊语言熵及概率语言等价变换函数，定义概率语言熵：

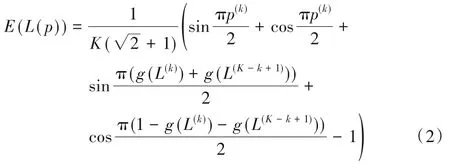
证明

1）首先对式子中的以下部分进行证明

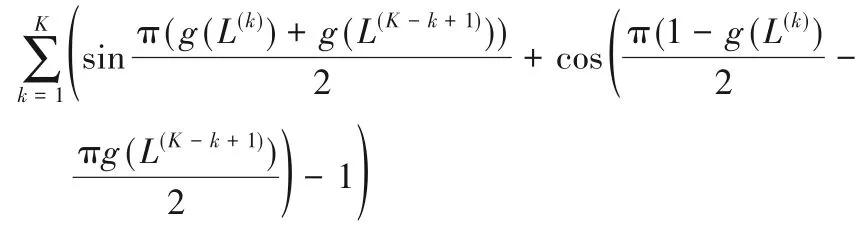
设 π(g(L(k))+g(L(K-k+1)))=a，a ∈[0，2π]，令 f(a)=所以可得-1 ≤f(a) ≤1。因此可将式（2）表示为：

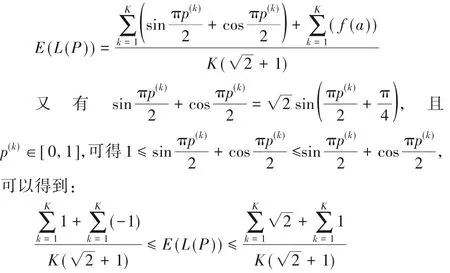
即：0 ≤E(L(p)) ≤1。 证毕。

2）当g(L(p))=0，p(k)=1时，

E(L(p))=

g(L(p))=1，p(k)=1时，

E(L(p))=

即当g(L(p))=0 或g(L(p))=1 时，若存在：p(k)=1，E(L(p))=0。 证毕。

定义3令S={sα|α=-τ，…，-1，0，1，…，τ}为一个语言术语集，L(p1)与L(p2)为两个概率语言术语集，其中#L(p1)和#L(p2)是这两个概率语言术语集的个数，并且#L(p1)=#L(p2)=K。那么L(p1)与L(p2)之间的交叉熵本文表示为CE(L(p1)，L(p2))需要满足以下条件：

1）CE(L(p1)，L(p2)) ≥0；

2）当且仅当g(L(p1)(k))=g(L(p2)(k))，k=1，2，…，K 时，CE(L(p1)，L(p2))=0。

基于犹豫模糊语言交叉熵及概率语言等价变换函数，定义概率语言交叉熵：

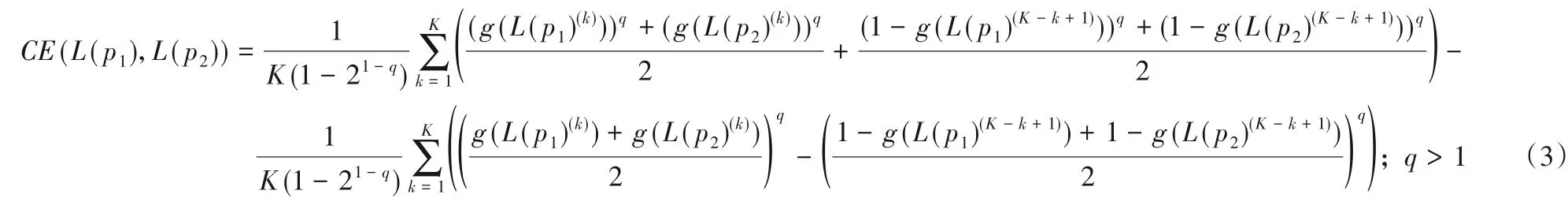
证明 令g(L(p1)(k))=x，g(L(p2)(k))=y，那么原式可表示如下：

CE(L(p1)，L(p2))=

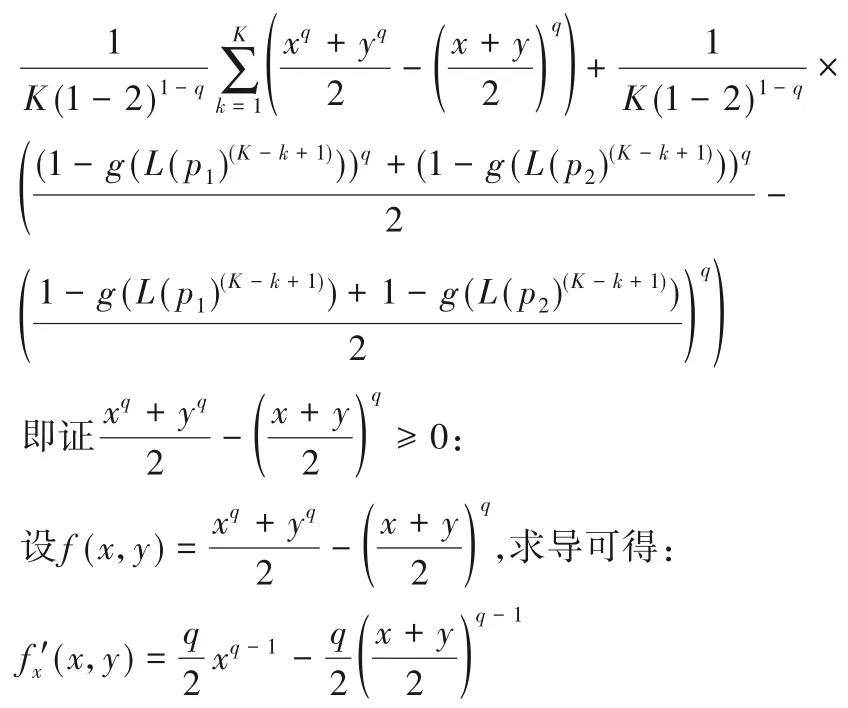
又x ∈[0，1]，y ∈[0，1]，所以f(x，y)在x ∈(0，y)上递减，在x ∈(y，1)上递增，y同理。故f(x，y) ≥f(x，x)=0，当且仅当x=y 成 立，即 g(L(p1)(k))=g(L(p2)(k))，k=1，2，…，K 时CE(L(p1)，L(p2))=0成立。 证毕。

1.2 群体满意度指数

针对后悔理论的效用函数，文献［13］在属性值为犹豫模糊元的多属性决策中提出一种群体满意度指数。本文将其拓展到属性值为概率语言术语集的多属性决策中。

定义4S={sα|α=-τ，…，-1，0，1，…，τ}为一个语言术集，L(p)为概率语言术语集，则称

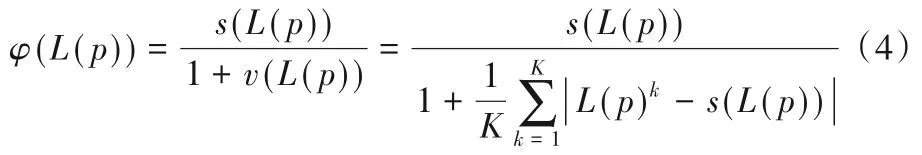
为概率语言术语的决策群体满意度指数。其中：s(L(p))表示概率语言术语集的得分函数，按照文献［2］中提出的得分函数公式进行计算；v(L(p))表示概率语言术语集L(p)的平均偏差函数，用来反映决策群体的分歧程度。

2 决策模型的构建

本章将在所提出的概率语言术语集的信息熵及交叉熵公式的基础上构建概率语言指标权重确定模型，该模型将用于计算所给出各决策指标的权重值，在此基础上，基于后悔理论的概率语言EDAS 排序模型也将在本章提出，该模型将后悔理论与EDAS 法结合，用于处理属性值为概率语言的应急决策问题。

2.1 问题的描述

假设某城市在同一时间爆发了多个网络舆情突发事件X={X1，X2，…，Xm}，因该城市应急资源有限，因此需优先处理综合危害性最高的突发事件，再依序处理剩余突发事件。假设应急部门选择了n 个评价指标c={c1，c2，…，cn}，且各评价指标的权重W=(w1，w2，…，wn)T未知，wj≥0(j=1，2，…，为了让评价结果的科学性更高，挑选有专业差异的专家组成决策组d={d1，d2，…，dl}。各决策专家为各突发事件的评价指标赋予语言评价值，最后综合各决策专家的评价矩阵，得到概率语言决策矩阵R=[Lij(p)]m×n表示如下：

其中的概率语言评价值表示为：

2.2 评价指标权重确定模型

信息熵描述的是信息的不确定程度，若某一评价指标所获得的熵值越小，则该评价指标所包含的信息越多，那么该指标在全局指标中也越重要，应赋予更大的权重值；若某一项决策指标上的交叉熵越大，则表示在该项指标上各备选方案的评价差异越大，那么该指标的重要性也越大，也应赋予更大的权重值。因此本文将采用各评价指标的评价值计算其信息熵及交叉熵，更加科学地计算出各评价指标的重要性程度，尽量避免人为赋权所带来的影响，让各评价指标最终所被赋予的权重更加合理且更加符合客观实际。本文将运用概率语言信息熵及交叉熵建立相应的指标权重模型，具体计算步骤如下：

1）利用式（2），计算评价指标cj的总体信息熵：

2）利用式（3），计算评价指标cj的平均交叉熵：则可得评价指标cj的总体交叉熵：

3）基于概率语言信息熵及交叉熵理论可知，评价指标cj平均概率语言交叉熵越大，该指标应赋予较大的权重值；若评价指标cj的概率语言总体信息熵越小，则该指标也应被赋予更大的权重值，可以得到如下评价指标权重优化模型：

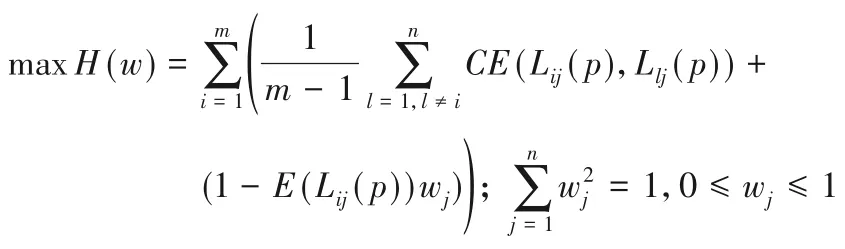
4）求评价指标权重优化模型，并进行归一化处理，可以得到各决策指标的标准权重如下：

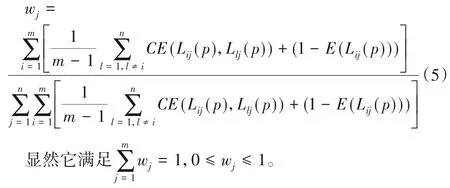
2.3 基于后悔理论的概率语言EDAS决策模型

经典的决策方法如TOPSIS、VIKOR 等，这些方法的逻辑功能是将最优解与负解的最大距离及将最优解与正理想解的最小距离作为最优解的基础。然而，EDAS方法的最佳选择是与平均解的距离相对应的，在EDAS 方法中，前两个度量值分别作为与平均值的正距离和负距离的传递，这些度量可以显示每个备选方案与平均解决方案之间的差异。相对于大多数其他多属性决策方法，EDAS法在不同权值下具有较好的稳定性，简单和较低的计算过程是也让其更适于应急决策问题的处理。此外，在应急决策这类不确定问题中，决策者的非理性行为因素应予以着重考虑，这不仅符合应急决策的实际情况，也可以得到更加合理、科学的决策结果。因此本节将考虑决策者后悔规避的心理行为，确定概率语言信息的效用值及欣喜和后悔值，让决策过程及结果更符合现实，然后结合EDAS法提出更适于应急决策问题的基于后悔理论的概率语言EDAS决策模型。具体步骤如下：

1）让各专家赋予各备选方案的各属性语言评价值，并获得概率语言决策矩阵R=[Lij(p)]m×n：

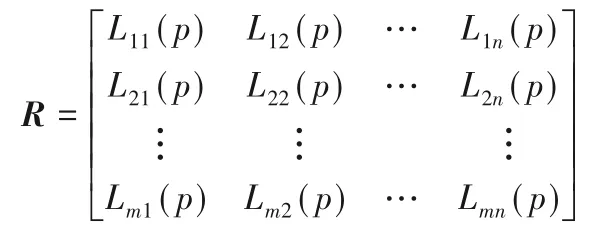
2）将概率语言决策矩阵进行标准化，根据文献［2］所提出的概率语言标准化公式，得到标准化后的概率语言决策矩NR=[Lij(p)]m×n：

3）根据式（5），计算各评价指标的权重值：

W=(w1，w2，…，wn)T

4）根据文献［22］提出的后悔理论的感知效用函数公式并结合式（4）计算各备选方案的后悔-欣喜值及感知效用值，并建立各方案感知效用值矩阵：

5）以感知效用值矩阵为计算目标，结合文献［18］所给出的EDAS方法计算步骤进行计算：

①计算各属性感知效用值的平均方案（AVerage solution，AV）：

AV=[AVj]1×n

②计算各属性感知效用值与平均值的正距离（Positive Distance from Average，PDA）：

PDA=[PDAij]m×n

与平均值的负距离（Negative Distance from Average，NDA）：

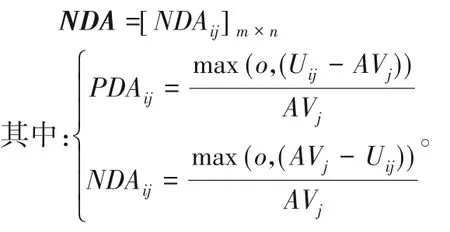
③计算加权后的PDA、NDA，可 得SPi（Weighted Summation of the Positive Distance）与SNi（Weighted Summation of the Negative Distance），其中：

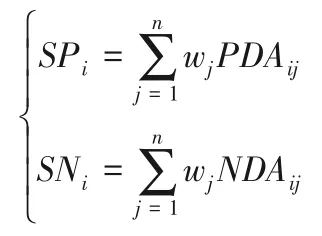
④标准化SPi与SNi，得到NSPi（Normalized Values of SPi）和NSNi（Normalized Values of SNi）：

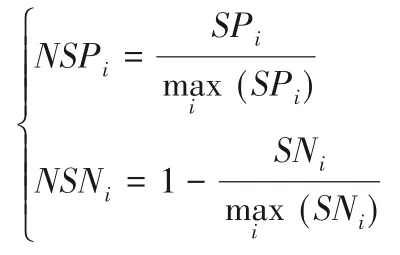
⑤得到各方案属性下的感知效用值的最终评估得分ASi（Appraisal Score）：

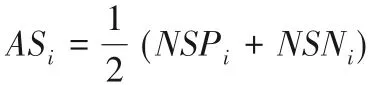
6）根据所得的各方案属性的感知效用值的最终评估得分，对各备选方案进行排序，选择出满意的方案。

3 算例分析

3.1 问题的描述

城市A 的网络舆情监测站点监测到可能爆发的3 个网络舆情突发事件X={X1，X2，X3}，因该地区应急资源有限，需优先处置综合危害性最高的突发事件，再依序处理剩余事件。为评估各网络舆情突发事件的综合危害性，本文根据文献［23-24］确定突发事件的广度c1、易爆度c2、扩散速度c3、可能持续时间c4、次生灾害发生作为评价指标c5，且评价指标的权重未知；选取5 位应急决策专家d={d1，d2，d3，d4，d5}组成应急决策委员会。

由于各决策专家受时间压力以及对网络舆情突发事件各信息掌握的不全面、不准确，往往难以及时地对各指标给出精确的评估值，因此允许决策专家为各突发事件的评价指标赋予语言评价值，决策者们利用S=｛s-3=极低，s-2=很低，s-1=低，s0=中，s1=高，s2=很高，s3=极高｝来评估各网络舆情突发事的评价指标，5 位决策专家评价各指标所得的原始矩阵如表1～5表示，其中“—”表示决策专家无法给出相应的信息，最终通过总结这五个表格可以得到概率语言决策矩阵R=[Lij(p)]m×n。

表1 决策专家d1给出的决策矩阵Tab.1 Decision matrix given by decision maker d1

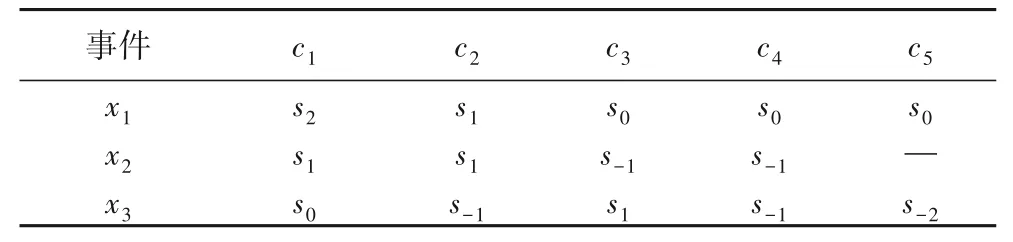
表2 决策专家d2给出的决策矩阵Tab.2 Decision matrix given by decision maker d2

表3 决策专家d3给出的决策矩阵Tab.3 Decision matrix given by decision maker d3

表4 决策专家d4给出的决策矩阵Tab.4 Decision matrix given by decision maker d4

3.2 方案的排序

1）让各专家赋予各备选方案的各属性语言评价值，并获得概率语言决策矩阵R=[Lij(p)]m×n，如表6。

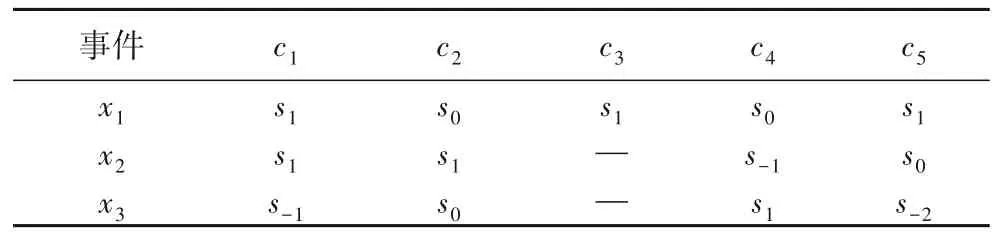
表5 决策专家d5给出的决策矩阵Tab.5 Decision matrix given by decision maker d5

表6 汇总后的概率语言决策矩阵Tab.6 Probabilistic linguistic decision matrix after summarization

2）将概率语言决策矩阵进行标准化，利用文献［2］，得到标准化后的概率语言决策矩阵NR=[Lij(p)]m×n，如表7。

3）根据式（5），计算各评价指标的权重值，得到评价指标的权重值：

W={0.128，0.246，0.327，0.145，0.154}

4）根据文献［22］并结合式（4），计算各备选方案的后悔—欣喜值及感知效用值，如表8，并建立各方案感知效用值矩阵。

5）根据文献［22］，计算各方案的感知效用值，取α=0.3，计算结果如表9。

6）以感知效用值矩阵为计算目标，结合EDAS 方法计算步骤进行计算：

①计算各属性感知效用值的平均方案值AV=[AVj]1×n，可得AV=［0.428 2，0.327 6，0.354，0.306 4，0.261 5］；

②计算各属性感知效用值与平均值的正负距离PDA=[PDAij]m×n、NDA=[NDAij]m×n：

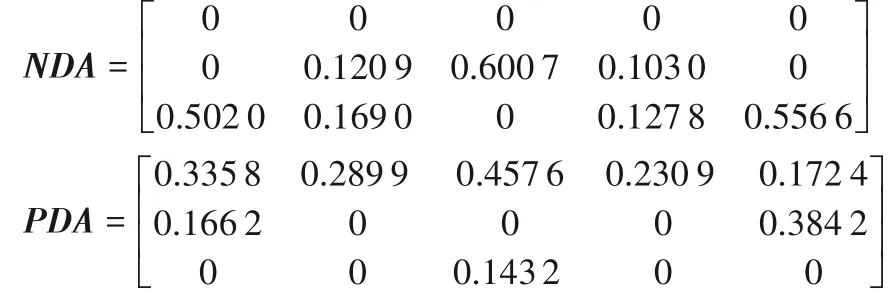
③计算加权后的PDA和NDA，分别得到SPi与SNi：

表7 标准化后的概率语言决策矩阵Tab.7 Probabilistity linguidtic decision matrix after standardization

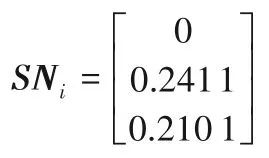
④将所获得的SPi与SNi进行标准化，得到NSPi与NSNi：

⑤计算各方案属性下的感知效用值的最终评估得分AS：

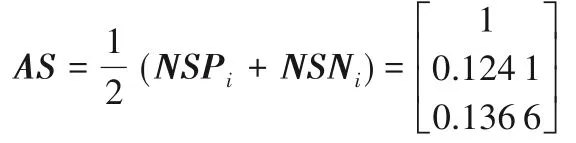
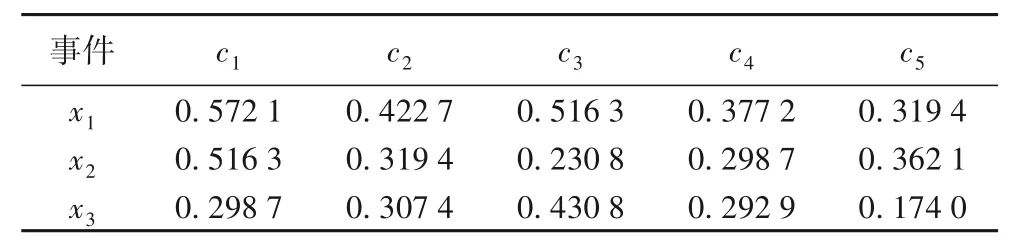
表8 各事件在不同评价属性值下的效用值Tab.8 Utility values of different events under different evaluation attribute values

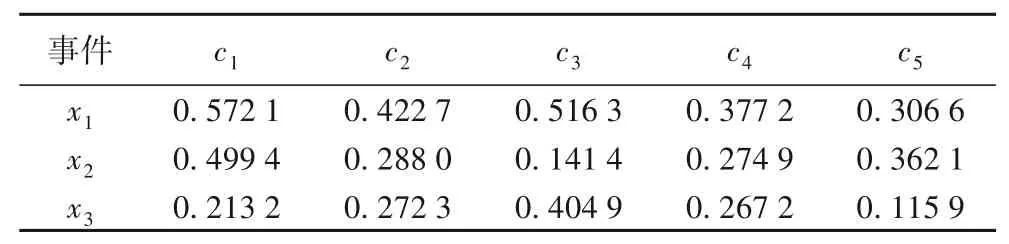
表9 各事件的感知效用值Tab.9 Perceived utility values of different events

7）根据最终的评估得分可以得到各网络舆情突发事件的排序为：

x1≻x3≻x2

因此可得到优先处置的事件为网络舆情突发事件1。

3.3 比较分析

本文将所提出的决策方法与其他文献提出的决策方法进行比较分析，主要将其他文献的决策方法分为两类：一是未考虑决策者后悔规避的心理行为，使用文献［2］方法对本文的实例进行分析；二是属性权重的赋值方法，使用文献［7，25］提出的权重赋值方法对本文的实例进行分析。

首先将本文所提出的决策方法与未考虑决策者后悔规避心理行为的决策方法进行比较。运用文献［2］的决策方法对本文实例进行排序所得到的结果为x1≻x3≻x2，与本文所提方法的排序结果相同。文献［2］所使用的决策方法虽然考虑了决策者对不同评价语言的不同偏好，但是却在决策过程中假设决策者是完全理性的，这一假设会在一定程度上偏离决策的现实情况，进而导致决策结果有失合理性。

然后是根据不同的属性权重确定方法进行对比分析。本文运用信息熵及交叉熵构建属性权重计算模型计算得到的各属性权重值为：

W=(0.128，0.246，0.327，0.145，0.154)

文献［25］运用传统熵权法计算各属性的权重，计算得到的各属性权重值为：

W=(0.221，0.187，0.294，0.195，0.103)

文献［7］运用线性规划法对各属性进行权重的赋值，计算得到的各属性权重值为：

W=(0.147，0.197，0.292，0.165，0.199)

那么使用文献［25，7］获得的属性权重值以及本文使用信息熵及交叉熵得到的属性权重值并分别使用EDAS 法和TOPSIS 法进行排序，使用这两种方法进行排序分析是为了让所得到的计算结果更具全面性，得到的最终排序结果如表10表示。

表10 使用不同权重计算方法的排序结果Tab.10 Sorting results by using different weighting methods

比较表10的三种不同赋权法产生的排序结果可知：

1）在三种赋权法下所得的最优先处置的事件都为网络舆情突发事件1，证明了本文方法具有一定的合理性。

2）不同赋权方法所得到排序结果的不同在于事件2 和事件3 的排序。文献［25］采用的是传统的熵权法，运用信息熵建立属性权重模型，造成排序结果与本文的排序结果有所差异，但最优先处置的事件都为事件1，这是因为该文献使用的熵权法求各属性权重时只使用各属性的信息熵进行计算而未将交叉熵考虑在内，因此造成一定的信息损失，对最终的排序结果产生影响。本文考虑到某项指标的信息熵测度越小，该评价指标所包含的信息越多，那么该指标在全局指标中也越重要，应赋予更大的权重值；若某项指标上的交叉熵测度越大，则表示在该项指标上评价差异越大，对决策评估的作用越大，也应赋予更大的权重值。因此本文未像传统的熵权法在求权重时只单纯考虑指标值的信息熵，而是将决策指标值的信息熵及交叉熵测度同时纳入权重确定模型中，不仅考虑了决策指标自身信息熵的大小对权重大小的影响，同时考虑了指标间的差异性程度信息即交叉信息熵，进而最大限度地减少原始信息的流失，使权重结果更具客观性、合理性。

3）文献［7］线性规划法得到的网络舆情突发事件的处置顺序本文的排序结果完全一致，说明本研究提出的权重确定模型具有一定的合理性，但需要指出的是，本文所提出的权重确定模型能够最大限度地保留原始信息特性，是具有一定优势的。

4 结语

本文考虑到在信息不完备、时间紧急的情况下，决策者很难及时地对网络舆情突发事件的各评价指标给出精确的评估值，提出一种基于概率语言的网络舆情突发事件应急群决策法，使评估过程更加符合应急情况下的客观实际，让评估结果更具合理性；同时考虑多个决策专家的评价意见，进行群决策探讨，使得决策过程及决策结果都不失科学性；通过概率语言信息熵及交叉熵构建指标权重确定模型，能减少信息的丢失，使权重结果更具准确性；在考虑决策者后悔规避这一心理行为下，结合EDAS 法提出一种计算更简要高效、计算结果更符合现实情况的决策方法；此外本文所提出的决策方法还适用于如安全事故、自然灾害应急预案等的应急评估，帮助决策者选择最佳应急方案，具有一定的实用意义。最后本文所提出的决策方法仅适用于有限个决策者进行决策的决策问题，未来将对相同背景下的大型群体决策问题进行探讨与分析。