牛顿-软阈值迭代鲁棒主成分分析算法

王海鹏，降爱莲，李鹏翔

（太原理工大学信息与计算机学院，山西晋中 030600）

（∗通信作者电子邮箱ailianjiang@126.com）

0 引言

主成分分析（Principal Component Analysis，PCA）作为一种常用的数据降维方法，在数据分析、目标检测、图像识别等领域得到了广泛应用。PCA算法能够提取目标数据的主要特征达到降维的效果［1］。如果数据含有稀疏噪声，PCA 提取的特征子空间会向噪声数据方向偏移。鲁棒主成分分析（Robust Principal Component Analysis，RPCA）是一种能够对具有结构信息但是被稀疏噪声破坏的数据矩阵进行分解的算法，找到隐藏在原始数据中的低秩成分，实际上就是找到了数据的本质低维空间。RPCA 不仅在特征提取中有着抵抗噪声的特性，而且在视频的背景前景分离［2-4］、鲁棒人脸识别［5］、移动目标检测［6］等领域也具有广阔的应用前景。

2011 年，Candès 等［7］首次定义了RPCA 问题，即将一个含有稀疏噪声的数据矩阵分解为低秩矩阵与稀疏矩阵两部分。为了保证稀疏矩阵足够稀疏，使用l0-范数进行约束，同时要使低秩矩阵的秩尽可能小。然而Gillis等［8］证明二进制矩阵（0-1矩阵）的分解是NP-Hard 问题，进而证明l0-范数约束最优化是一个NP-Hard 问题。由于l0-范数无法使用凸优化解决，文献［7］将RPCA 问题的低秩与稀疏约束松弛为核范数与l1-范数约束的目标函数最优化问题，并用拉格朗日方向交替法［9］求解。由于该算法每次迭代需要对数据进行奇异值分解求核范数，因此该算法的时间复杂度非常高［4］。Shen 等［10］提出了基于增广拉格朗日方向交替法的低秩矩阵拟合（Low-Rank Matrix Fitting，LMaFit）算法，该算法用两个低秩矩阵的乘积表示一个低秩矩阵的方法代替核范数，降低了因使用奇异值分解而产生的时间开销。这种方法是后续研究中降低时间开销的重要方法。Yi 等［11］提出基于梯度下降（Gradient Descent，GD）的RPCA 算法，该算法使用稀疏矩阵估计算子估计出原始数据的稀疏矩阵的近似矩阵。GD 算法在优化算法上选择了梯度下降，提高了算法的运行效率。Lu 等［12］推导出了张量核范数、张量软阈值算子，并以此构建数学模型，采用方向交替拉格朗日乘子法实现了张量鲁棒主成分分析（Tensor Robust Principal Component Analysis，TRPCA）算法，该算法提高了RPCA 算法对彩色图像处理、视频背景建模的能力。TRPCA 算法因为使用了张量奇异值分解，因此时间复杂度较高。Chereau 等［13］提出了基于最大相关熵模型的RPCA 算法，他们采用了幂迭代的方式来求解最大相关熵模型，进而实现RPCA 算法。该算法的优点是不需要预先设置低秩矩阵的主成分的数量，提高了算法的易用性。由于上述RPCA 算法的计算时间随着数据规模提高而显著提升，处理大规模数据会消耗大量的时间，因此本文将针对RPCA 问题，通过改进RPCA 模型，降低RPCA 算法的时间复杂度，进而降低数据规模对RPCA算法的影响，提高RPCA算法的运行速度。

1 RPCA问题及模型

由于主成分分析算法是由欧氏距离最小化推导出的算法，因此稀疏噪声会因为欧氏距离的二次方特性对主成分分析算法求得结果产生较大的影响［14］。

图1（a）展示了PCA 算法在数据较均匀的条件下的效果，从图中可以看出，PCA 能够准确地对这些分布均匀的数据降维。如果数据含有稀疏噪声，如图1（b），PCA 算法的结果会产生较大的偏差。RPCA 算法提取了含有稀疏噪声数据的主要特征，并且对该含噪数据进行了降维。

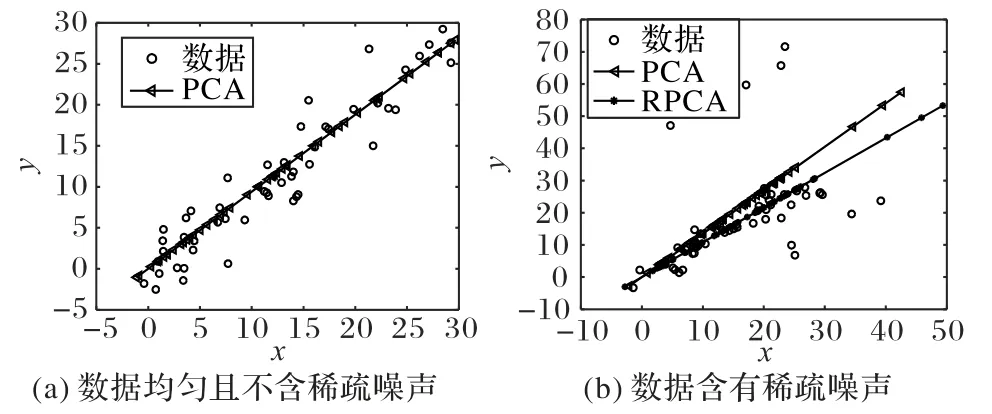
图1 PCA算法与RPCA算法对比Fig.1 Comparison of PCA algorithm and RPCA algorithm

为了将含噪数据分解为低秩矩阵和稀疏矩阵，同时使低秩矩阵的秩与稀疏矩阵的非0 元素的数量尽可能少，文献［7］中将RPCA模型表示为：

其中：Y表示包含稀疏噪声的数据，L表示数据中的低秩部分，S 表示数据中的稀疏部分，rank(L)表示L 的秩，模型（1）满足Y=L+S。模型（1）理论上可以达到分离低秩矩阵和稀疏矩阵的目的。然而l0-范数是一种无法使用凸优化求解的范数。为了优化模型（1），因此使用核范数与l1-范数将模型（1）松弛化为：

2 NSTI模型及其优化算法分析

本文改进原有RPCA 模型，提出了一个新的RPCA 模型，使得该模型在能够表示RPCA 问题的基础上又能够采用简单高效的方法进行优化，该优化方法称为牛顿-软阈值迭代（Newton-Soft Threshold Iteration，NSTI）算法。

2.1 NSTI算法模型

为了降低因计算奇异值分解而导致的巨大的算法运行时间的开销，LMaFit和GD算法使用了如式（3）所示的方法：

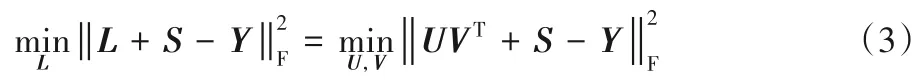
其中U、V 是两个低秩矩阵，满足L=UVT。鉴于这种利用两个低秩矩阵的乘积表示一个低秩矩阵的方法，可避免使用核范数，本文改进模型（2），并给出NSTI算法的数学模型：

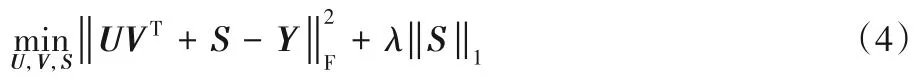
式（4）左边的范数中，低秩矩阵L由两个低秩矩阵U、V 的乘积表示，因为rank(L)=min(rank(U)，rank(V))，所以能够保证L 是一个低秩矩阵。式（4）左边是一个能够对U、V 进行凸优化求解的范数，本文用牛顿法来优化左边的范数。采用牛顿法求解的原因有两个：第一，牛顿法比梯度下降收敛速度更快；第二，不会因为使用了牛顿法而增加过多的时间开销。

式（4）右边稀疏矩阵S 通过l1-范数来表示其稀疏性质。l1-范数是l0-范数的凸近似。最小化l1-范数的目的是为了让S稀疏化。本文采用软阈值迭代算法求解稀疏矩阵S。该方案相对于文献［11］中的GD 算法的稀疏矩阵估计算子，具有计算速度快的优点。软阈值迭代算法的缺点是软阈值是静态的，并且需要在算法运行之前根据数据调整软阈值的大小。本文提出了软阈值估计算子，用来弥补软阈值迭代算法中的不足。

2.2 NSTI算法

NSTI算法分为两部分，其中一部分是求解稀疏矩阵S。S对于模型（4）的梯度为：

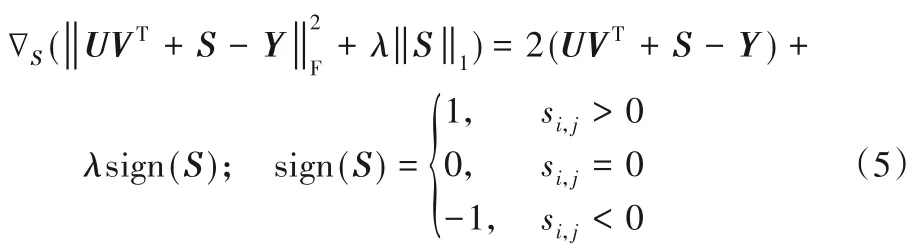
由软阈值迭代算法［15］，可求出稀疏矩阵S 的近似解。式（6）是软阈值算子也是S近似解的计算式。

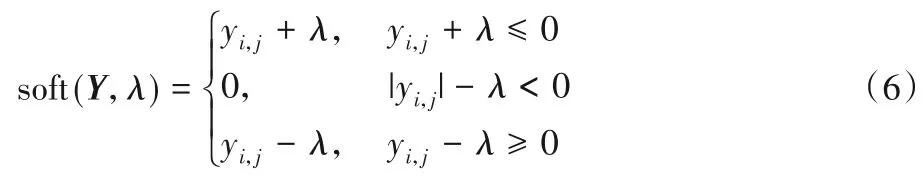
NSTI 算法的另一部分是求解低秩矩阵的两个因子U、V。U、V对于模型（4）的一阶梯度为：

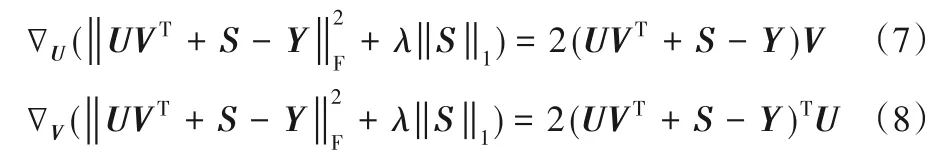
Hessian 矩阵是牛顿法求解的关键，通过计算出Hessian矩阵，就能利用牛顿法求出低秩矩阵U、V。U、V 矩阵对应的Hessian矩阵为：

因此，可得到如下两式：

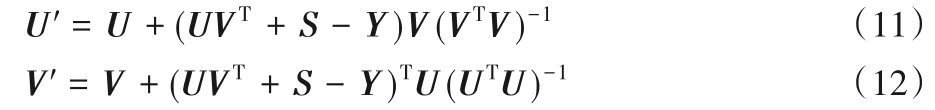
NSTI算法详细过程如下。

输入 数据Y，精确度α，收敛阈值t，秩r；

输出 U、V、S。

1）首先对Y 进行奇异值分解，选取前r个奇异值与前r个左奇异向量的乘积初始化U，选取前r 个奇异值与前r 个右奇异向量的乘积初始化V。稀疏矩阵S为0矩阵。

2）计算Y'=Y -UVT，并计算软阈值λ=f(Y'，α)。

3）利用软阈值迭代求出稀疏矩阵S=soft(Y'，λ)。

4）计算矩阵E=Y'-S，以及U、V 的Hessian 矩阵的逆

NSTI 算法思想借鉴了方向交替法。将模型（4）中要求的3 个变量分为两部分，通过交替迭代求解模型中的3 个变量。2.1 节提到牛顿法比梯度下降收敛速度更快，软阈值迭能够快速求解稀疏部分，因此NSTI采用牛顿法与软阈值迭代交替计算的方案来优化模型（4）。该方案能够求解模型（4）中的3个变量并且算法的收敛速度与计算速度都得到了提升。

2.3 软阈值估计

软阈值λ 决定着数据Y 中的数据的划分：λ 值越低，每次迭代，能提取更多的元素成为稀疏矩阵，然而这样会使得原本属于低秩矩阵的成分被划分到稀疏矩阵中，优点是能够提高算法的精确度；反之，λ 值越高，将提高低秩矩阵元素的比例，优点是能够降低算法迭代次数。如果λ 值过高，那么最终收敛的结果会将全部元素划分到低秩矩阵L中，稀疏矩阵S将会是一个0矩阵；反之，λ值过低，那么全部元素将划分到稀疏矩阵S中，L矩阵将变成一个0矩阵。软阈值计算方式为：

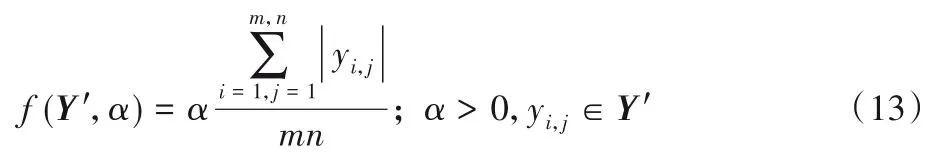
对任意属于Y'(Y'=Y -UVT)的元素a1、a2，通过和阈值λ 比较，小于阈值λ 的则被归到低秩成分L 中，大于λ 的被归到稀疏成分S中。如果|a1|＜|a2|，而且一定存在低秩成分，那么a1比a2更有可能是低秩成分，低秩空间UVT的元素被认为是其对应原始数据Y 的元素在低秩空间的投影，原始数据减去其在低秩空间大的投影的绝对值是原始数据元素到低秩子空间的距离。将数据扩展到Y 全部元素，对于任意ai(i=1，2，…，mn -1，mn)，一定存在这样的一个序列，其中ai与bj是一一对应关系。通过式（13）估计一个λ，将数据中距离平面较近的一部分划分为一个低秩矩阵，将距离平面较远的数据部分划分为一个稀疏矩阵。通过调节α 的大小控制λ 的大小，进而控制算法的精确度。

2.4 NSTI时间复杂度分析

假设数据Y 是一个m × n 的数据矩阵，Y=L+S，L 是一个m × n 的矩阵，L 矩阵的秩为r，r 远小于m 和n。假设矩阵U、V 的规模分别为m × r，n × r，那么L 的秩最大为r。对于稀疏矩阵S，S的规模为m × n。

基于上述假设，奇异值分解的时间复杂度为O(n2m)，初始化U、V 矩阵的过程为O(mr)，因此初始化过程时间复杂度为O(n2m)。

在算法迭代过程中：第2）、3）步时间复杂度为O(nm)；第4）步求解Hessian 矩阵时，需要计算的时间复杂度为O(mnr)，在求Hessian 矩阵的逆矩阵中，因为Hessian 矩阵的规模时r ×r，所以Hessian 矩阵的逆运算开销可以忽略；同理第6）步中的时间复杂度为O(mnr)。因此每次迭代复杂度为O(mnr)，软阈值估计算子的时间复杂度为O(nm)。假设算法迭代x次收敛，则算法完整的时间复杂度为O(xnmr)，因为r远小于m 和n，因此算法时间复杂度近似为O(xnm)。

3 实验与分析

3.1 实验环境

实验选取NSTI 算法、LMaFit 算法和GD 算法三个算法进行对比。LMaFit、GD 是文献［16-17］评价认可的效率较高的两个算法。通过与LMaFit算法和GD算法对比来证明NSTI算法时间效率和算法精确度的提高。实验环境为Matlab 2019a，实验机器配置为Intel Core i7 8700，6 核心12 线程，内存为8 GB，操作系统为Windows 10。在实验中的奇异值分解函数为PROPACK 数据分析工具包中的lansvd 函数。基于lanczos分解的lansvd 奇异值分解函数具有比传统奇异值分解函数更快的计算速度。

3.2 算法有效性分析

为了验证算法是有效的，将从算法的整体损失、低秩矩阵损失和稀疏矩阵损失三个角度来说明。算法整体损失为l，l越小说明算法越精确，提取的稀疏矩阵越稀疏。其中l为：

决定数据Y 规模的参数有m、n 和低秩矩阵的秩r 以及稀疏矩阵的非0元素的比例a，其中数据Y=L+S。低秩矩阵L中的元素生成过程如下：首先生成一组基向量，选择r 个基向量，随机组合生成一个m × n 的秩为r 的低秩矩阵L。然后利用a 随机生成一个稀疏矩阵S，该实验使用Matlab 内置函数sprand。

实验数据的规模设为1 000×1 000，低秩矩阵的秩为20，稀疏矩阵的稀疏度为0.2。图2（a）显示随着迭代次数增加，算法整体与各部分逐渐收敛。NSTI 算法借鉴了方向交替法的思想，每次迭代求出一组参数，作为下次迭代的输入。算法每次迭代，都能够降低算法的整体损失与各参数的损失，最终达到算法的整体收敛。图2（b）中验证了算法能够正确地求出一个符合输入数据的稀疏度的稀疏矩阵。算法在迭代初期，计算出的稀疏矩阵包含大量的非0 元素，但随着算法迭代，稀疏矩阵收敛于原始的稀疏矩阵。

图2 NSTI算法运行效果Fig.2 Running effect of NSTI algorithm

3.3 算法性能对比

为了验证NSTI 算法的时间效率的提升。设计实验对比三种算法在同一数据下经过迭代达到相同的损失l 所需要的运行时间。

图3 是三种算法在相同规模的数据下运行时间的对比，说明了NSTI 算法比LMaFit 算法、GD 算法，运行速度要快，运行时间稳定。

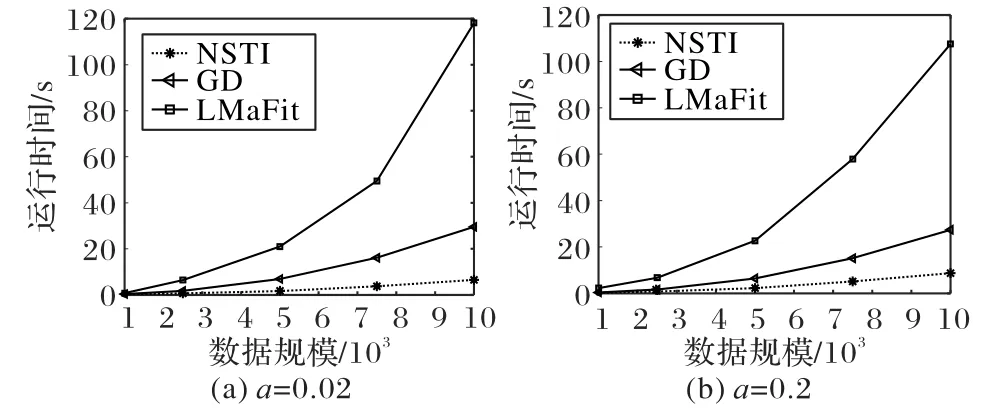
图3 三种算法在不同数据规模下的对比Fig.3 Comparison of three algorithms under different data sizes

LMaFit 的单次迭代时间复杂度为O(n3)，GD 算法的单次迭代时间复杂度为O(n3)，NSTI 算法单次迭代时间复杂度为O(n2)，所以NSTI的计算时间相对LMaFit、GD增长缓慢。在算法机理上，NSTI 选用的牛顿法，在理论上比梯度下降收敛速度快，又因为RPCA 问题的低秩的特性，牛顿法的计算速度由O(n3)变为O(n2)，所以牛顿法比梯度下降法计算速度快。NSTI选择的软阈值迭代法理论上时间复杂度为O(n2)，在保证算法准确度的同时，保证了算法的时间效率。

图4 是当非0 元素比例a=0.1，数据规模为5 000×5 000，通过调整低秩矩阵的秩r，对数据进行矩阵分解，对比三个算法在达到相同的损失l所需要的时间：当r ＜8时，NSTI算法与GD 算法运行时间比较稳定；当r ≥8时，三种算法的变化规律逐渐接近。

由于算法机理的不同，NSTI、GD 与LMaFit 单次迭代的时间随着r提升而小幅提升，然而LMaFit的迭代次数随着r的提升而降低，进而降低了计算时间。如图4，NSTI 与GD 算法略有提升，LMaFit算法有明显下降。

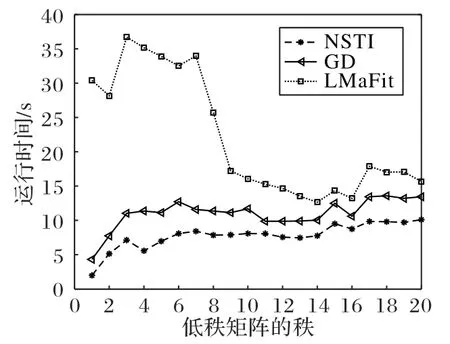
图4 三种算法在不同低秩r下运行时间对比Fig.4 Comparison of running time of three algorithms under different low rank r conditions

图5 展示了NSTI 对比其他算法的时间效率提升百分比，图5的数据来源是图4。通过图5可以看出，NSTI算法在秩为1 时相比较GD、LMaFit 算法，能够分别提升54.0%与93.5%的时间效率；当秩为20 时，能够分别提升24.6%与45.5%的时间效率。

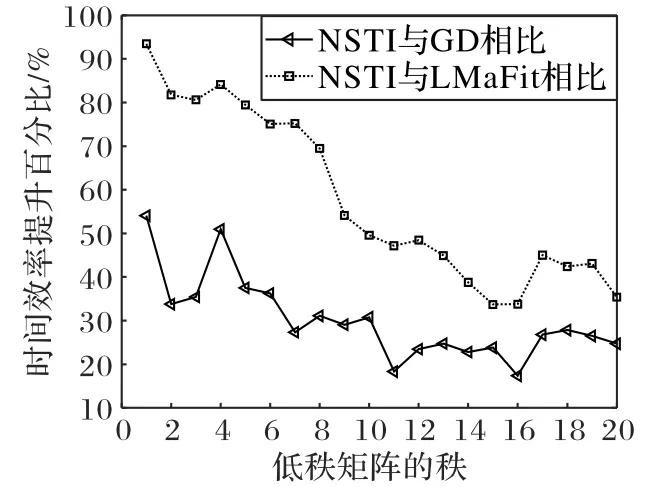
图5 与对比算法相比NSTI的性能提升Fig.5 Performance improvement of NSTI compared with comparison algorithm

3.4 视频背景/前景提取实验

为了验证NSTI算法在视频前景背景分离的能力，设计实验对比算法在视频背景/前景提取中的效果。将视频看做数据Y，视频的背景看作是低秩矩阵L，视频的前景看作是稀疏矩阵S［15］。对视频的数据矩阵进行RPCA，得到低秩矩阵和稀疏矩阵。低秩矩阵输出为背景，稀疏矩阵输出为前景。图6为该实验要处理视频的第40、70、100帧。

图6 原始视频Fig.6 Original video

图7 展示不同算法提取的背景。对比提取的背景，在第70帧和第100帧中原画汽车的位置，GD算法与LMaFit算法出现黑影，在NSTI 算法对应的位置没有黑影，色彩与原始图像的色彩基本一致，这说明NSTI 算法提高了去除噪声的能力。在右侧栏杆位置，LMaFit 算法将栏杆全部划分到前景，NSTI算法，GD算法将栏杆算作背景。

图8 中的GD 和LMaFit 算法出现一个NSTI 算法中没有出现的图块。对比9 张提取的前景图片，NSTI 算法相对GD、LMaFit 算法，提取的视频前景最完整。表1 说明NSTI 算法比其他算法的运行时间效率至少提高了78.7%。

RPCA 算法能够将数据分解为一个低秩矩阵和一个稀疏矩阵，进而将视频分解为背景与前景。又因为该视频数据的背景的秩为1，因此能够保证NSTI 算法的牛顿法部分的时间效率最高。NSTI 采用了软阈值迭代法，同时用软阈值估计算子确定软阈值，这种改进了的软阈值迭代算法能够求出更加精确的稀疏矩阵，因此可以从数据中看出NSTI算法求出的前景更加精确。

图7 不同算法提取的背景对比Fig.7 Comparison of background extracted by different algorithms

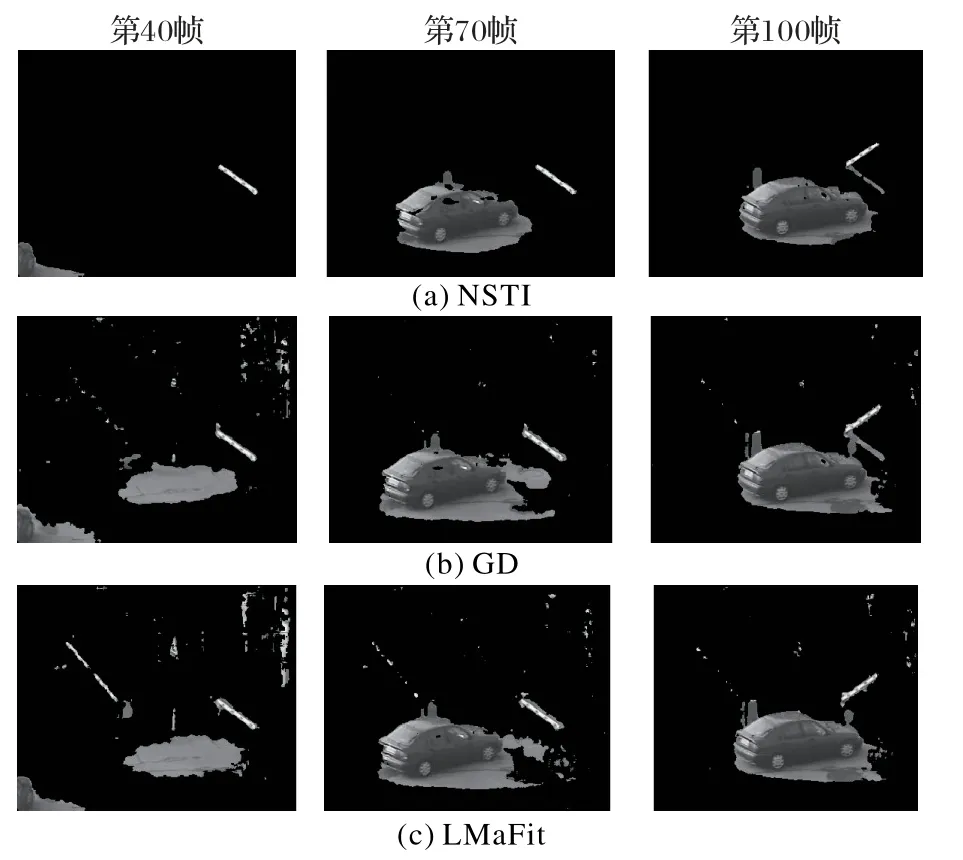
图8 不同算法提取的前景对比Fig.8 Comparison of foreground extracted by different algorithms

表1 各算法消耗的时间 单位：sTab.1 Time consumed by different algorithms unit：s

3.5 图像降噪实验

为了证明算法在图像降噪的能力的提升，本实验对一组a=0.2含噪图片进行降噪。实验数据共有10张含噪图片。图像降噪实验中，原始图像被视为低秩矩阵L，噪声被视作稀疏矩阵S，通过RPCA 处理达到降噪效果。本实验将对比算法的运行时间以及算法的残差e，利用残差对比算法的精确度高低，e越小精确度越高。e的计算方式为：

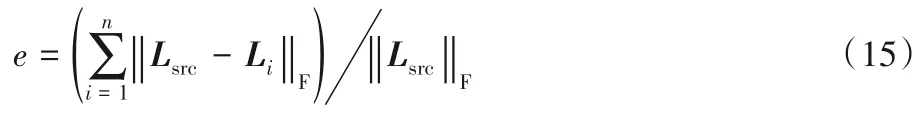
其中：L表示图片的数据矩阵，Lsrc表示原始图片，Li表示第i幅含噪图片降噪后的结果。该实验采用峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）［12］来评价算法的降噪能力。

图9 的数据说明了NSTI 算法的输出结果噪点最少，相比GD和LMaFit，NSTI的图像更加清晰。表2的数据说明了NSTI的残差值比其他算法至少降低了45.3%。NSTI算法的时间效率比其他两个算法至少高出64.3%。NSTI算法计算得到的图片的PSNR 值比LMaFit 算法高出18.8%，比GD 算法高出24.8%。因此可以说明NSTI算法处理的图像更加清晰。

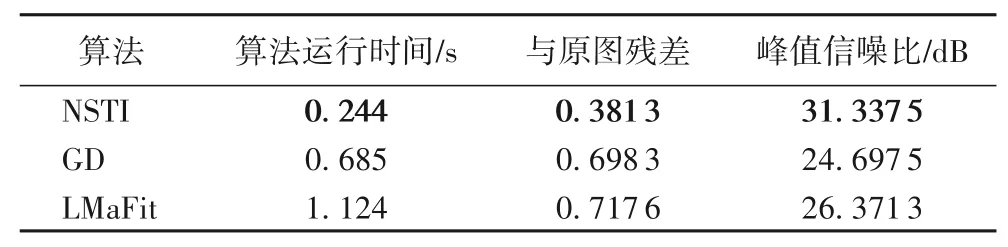
表2 图像降噪实验Tab.2 Image denoising experiment

图9 图像降噪实验Fig.9 Image denoising experiment

因为NSTI算法提高了算法效率，所以在处理图像数据更加高效，NSTI 算法比LMaFit 算法提高的时间效率为78.29%，与图5的数据相符合。NSTI算法采用了改进的软阈值迭代算法，不需要预估稀疏度，相比较稀疏矩阵估计算子，提高了图像降噪的水平，PSNR高达31.337 5 dB。

3.6 图像恢复实验

为了验证NSTI 算法在图像恢复方面的能力设计人脸恢复实验，选取的对比算法有GD、LMaFit、TRPCA 算法，数据集为耶鲁大学的人脸数据集。耶鲁大学的人脸数据包含面部的不同表情、光影、方向及佩饰的图像。

图10 4种算法的图像恢复效果对比Fig.10 Image recovery effects comparison among four algorithms

表3展示了各个算法分别处理得到的图像的PSNR 的值，PSNR 值越大，说明算法的恢复图像能力越强。图10 验证了NSTI算法能够有效地恢复图像。与LMAFit相比，NSTI的时间效率与PSNR 值比较高，这一点在表3 中得到验证。NSTI，GD与TRPCA算法的PSNR值在表3中无明显区别，这说明对于耶鲁大学数据集，NSTI、GD 与TRPCA 三种算法的图像恢复能力基本一致。因为NSTI算法使用了牛顿法与软阈值迭代法，所以在时间效率上，NSTI比另外三种算法要高，能够快速地计算出人脸的低秩特征。表3证明了NSTI有着最高的时间效率。

NSTI 算法比其他算法的时间效率高的原因有两点：第一，GD 算法每次迭代需要求解稀疏矩阵估计算子，该算子的时间复杂度为O(n3)；LMaFit算法每次迭代都需要计算奇异值分解，奇异值分解的时间复杂度为O(n3)；TRPCA 算法存在张量核范数的运算，张量核范数的时间复杂度O(n3)。第二，NSTI采用了牛顿法与软阈值迭代法提高计算速度，NSTI每次迭代时间复杂度为O(n2)。

表3 不同算法图像恢复性能对比Tab.3 Comparison of image restoration performance of different algorithms

4 结语

本文研究了RPCA 问题，利用牛顿法和软阈值迭代法改进了RPCA模型，并提出了NSTI算法。经实验证明，本文提出的NSTI算法，与其他RPCA算法相比，在时间效率与算法精确度上有明显提升。本文提出的软阈值估计算子能够计算出一个动态且精确的软阈值，能够提高NSTI算法的收敛速度和精确度。NSTI算法也存在着不足，像GD 算法一样，参数中需要输入低秩r，来决定低秩矩阵的秩r，而没办法在算法中直接估计出r的大小。