基于Rescaled Hinge损失函数的多子支持向量机

李 卉，杨志霞

（新疆大学数学与系统科学学院，乌鲁木齐 830046）

（∗通信作者电子邮箱yangzhx@xju.edu.cn）

0 引言

分类问题是机器学习中研究的热点问题之一，针对此问题Vapink 在VC（Vapnik-Chervonenkis）维和统计学习理论的基础上提出支持向量机（Support Vector Machine，SVM）［1］。与其他机器学习方法（例如人工神经网络［2］）相比，支持向量机具有许多优势。首先，支持向量机解决一个凸二次规划问题，确保一旦获得最佳解，它就是唯一解。其次，支持向量机通过最大化两个类之间的间隔来得出模型，并基于结构风险最小化原则，而不是经验风险最小化原则。目前，支持向量机已应用于不同领域，例如疾病诊断［3-4］、文本分类［5］和企业信用等级［6］等。

鉴于支持向量机优越的性能，迄今为止它的扩展版本得到了长足发展。2007 年，Jayadeva 等［7］提出一种基于非平行分划超平面思想的双支持向量机（TWin Support Vector Machine，TWSVM）。双支持向量机与广义特征值中心支持向量机［8］的想法相似，都针对给定训练集生成两个非平行超平面解决二分类问题，但优化问题的构造不同。由于这两个方法都是基于非平行超平面的思想构造最终的决策函数，从而使得学习机具有更好的灵活性和泛化能力。最近，双支持向量机的一些扩展算法也被不断提出，如文献［9-10］。然而，在现实生活中有许多需要解决的问题为多分类问题，如图像分类［11］、疾病分类［12］、蛋白质折叠识别［13］等。以双支持向量机为基础，文献［14］提出多子支持向量机（Multiple Birth Support Vector Machine，MBSVM）解决多分类问题。多子支持向量机通过求解K 个小规模二次规划问题来得到决策函数，从而有较低的计算复杂度，针对多分类问题具有一定的优越性。

另一方面，在现实生活中，收集到的数据往往带有噪声，或者标签记错，这样的数据称之为异常值。多分类算法在遇到异常值的情况下，算法的性能会有所下降。有很多研究处理异常值都是通过对数据进行预处理，直接剔除异常值；然而直接剔除异常值会出现信息丢失等问题。因此，在不删除异常值的前提下，提出鲁棒的分类方法成为热门的研究。例如，文献［15］提出求解有噪声数据的二分类方法，称作基于Rescaled Hinge损失函数的鲁棒支持向量机（Robust Support Vector Machines based on Rescaled Hinge loss function，RSVM-RHHQ）。

为了提高多分类方法对异常值的鲁棒性，本文提出基于Rescaled Hinge 损失函数的多子支持向量机（Multiple Birth Support Vector Machine based on Rescaled Hinge loss function，RHMBSVM）。该方法通过将有界、非凸的Rescaled Hinge 损失函数引入多子支持向量机的优化问题中，从而得到鲁棒的优化问题。事实上，该方法是一个加权多子支持向量机。给每个点不同的惩罚，从而可识别异常值，提高鲁棒性。其次，针对K 个非凸优化问题，通过共轭函数理论将问题进行等价转换，利用变量交替策略构造迭代算法，使问题得到了有效求解。本文方法主要的优势和特点可总结为如下3个方面：

1）针对多类分类问题，本文方法使用了非平行分划超平面的思想，所构建的优化模型只需求解K 个小规模的二次规划问题，主要求解对偶问题的未知量个数只与第k 类样本点的个数有关，有效降低了计算复杂度。

2）针对带异常值的多类分类问题，本文方法通过将Rescaled Hinge 损失函数引入到多子支持向量机中，给每个样本点不同的惩罚，从而减弱异常值对模型性能的影响。

3）针对线性情形和非线性情形的多类分类问题，本文方法分别给出了具体的优化模型和求解算法。具体地，当多类分类问题只需超平面就可分划时，使用线性情形的算法；否则，就使用引入核函数的非线性情形的算法。值得注意的是，当非线性情形选择的是线性核时，算法即可退化为线性情形。

数值实验结果表明，在无异常值的UCI数据集中，本文方法的正确率比现有的多分类方法高。在有异常值的UCI数据集中，本文方法的鲁棒性优于现有的多分类方法。

1 准备知识

本章介绍了多子支持向量机和Rescaled Hinge损失函数。给定训练集：

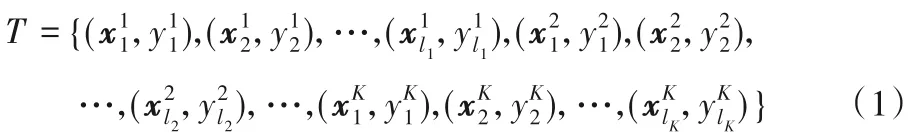
1.1 多子支持向量机

多子支持向量机的思想是针对训练集T（1）寻找K个超平面，第k个超平面具体形式如下：

多子支持向量机通过求解K个小规模二次规划问题来得到式（2）所示的超平面。其原理是第k类样本点离第k个超平面尽可能远，其余K -1 类样本点离第k 个超平面尽可能近，从而可构造多子支持向量机的第k个小规模二次规划问题：

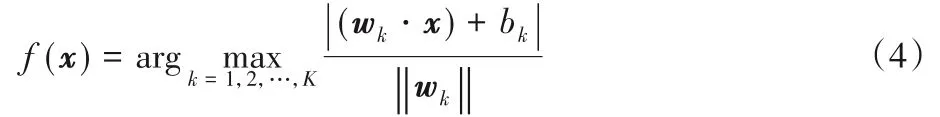
1.2 Rescaled Hinge损失函数

在本节中，简单介绍一下Rescaled Hinge损失函数［15］。在文献［16］中，用Correntropy［17］得到的损失函数C-loss为：

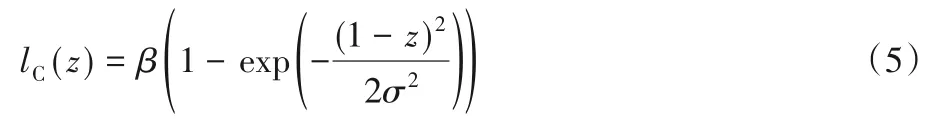
其中σ 是窗宽，常数当z=0 时，lC(0)=1。若定义最小二乘损失函数lls(z)=(1-z)2［18］，损失函数C-loss可写为：

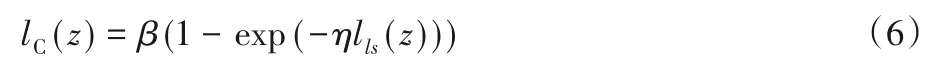
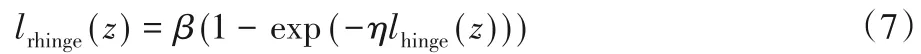
其中lhinge(z)=max(0，1-z)，当z=0时，lrhinge(0)=1。

图1［15］展示了Hinge 损失函数和不同η 的Rescaled Hinge损失函数的直观几何图像。

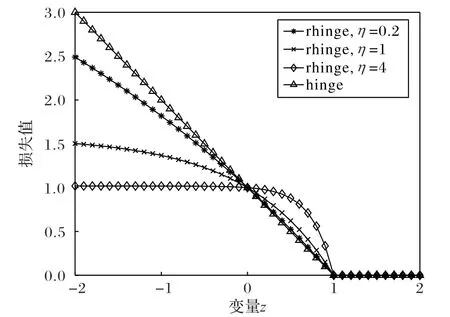
图1 Hinge损失函数和不同η值Rescaled Hinge 损失函数Fig.1 Hinge loss function and Rescaled Hinge loss function with different η

从图像可看出Hinge 损失函数和Rescaled Hinge 损失函数都是单调函数，而Hinge损失函数是凸函数，Rescaled Hinge损失函数是非凸函数。从图中也可看出，η 的值越接近0，Rescaled Hinge损失函数就越接近Hinge损失函数。

2 模型的提出

针对带有异常值的多分类问题，本文提出基于Rescaled Hinge 损失函数的多子支持向量机（RHMBSVM）。该方法包括线性情形和非线性情形：线性情形针对超平面能够分划的多类分类问题提出，最终的决策函数由K 个超平面构成；否则，本文通过引入核函数，构造非线性情形的优化模型，从而可得到K 个超曲面来构造最终的决策函数。值得注意的是，当非线性情形时，如果选择线性核函数，模型可退化为线性情形。

2.1 线性情形

现给出直观的线性情形的优化模型和求解过程。给定训练集T（1），构造如下K个超平面：

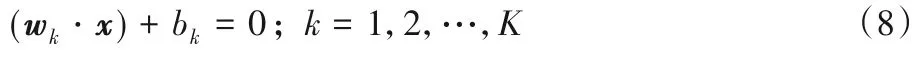
为了得到上述超平面，构造如下原始优化问题：

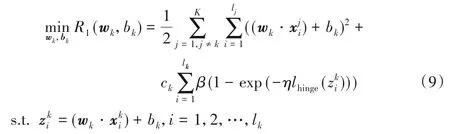
其中ck≥0 是惩罚参数。优化问题（9）中，目标函数的第一项表示除了第k类样本以外的K -1类样本离第k个超平面尽可能近，第二项表示第k类样本离第k个超平面尽可能地远。为了使不同的样本赋予不同的权重，这里使用了有界、非凸的Rescaled Hinge损失函数。

现在给出求解优化问题（9）的求解过程，由于β 是常数，对优化问题（9））没有影响，因此优化问题（9）等价于下面的优化问题：

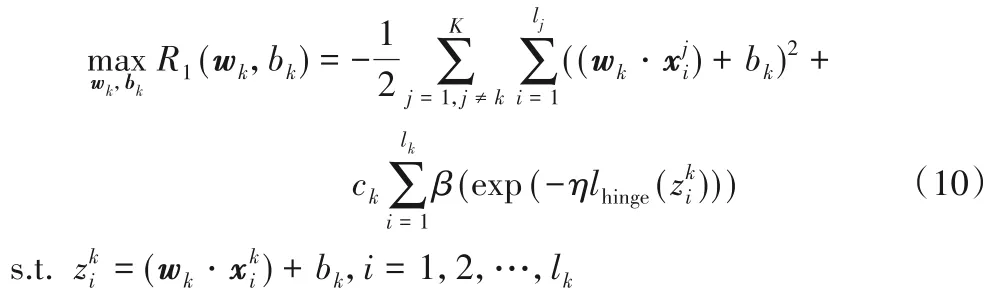
由于引入非凸的Rescaled Hinge 损失函数，导致优化问题（10）为一个非凸的优化问题，不方便求解，因此，通过共轭函数理论对优化问题（10）进行等价转换，再采用变量交替策略得到优化问题（10）解(wk，bk)。具体地，引入辅助函数h(v)=-v ln(-v)+v(v ＜0)，根据共轭函数理论［19］，h(v)的共轭函数为：

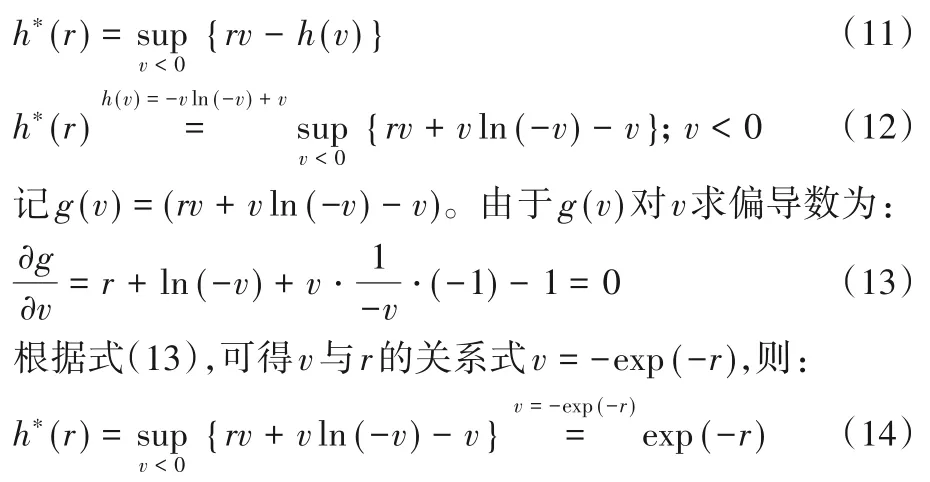
接下来，将共轭函数理论应用到需要求解的非凸优化问题（10）中。

由于求解式（18）的上界，等价于求解式（18）的最大值。因此，优化问题（10）等价为如下形式：

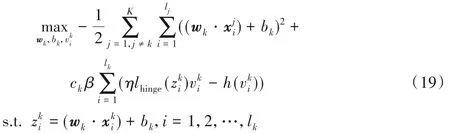
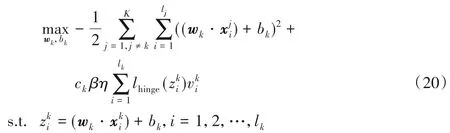
此时，式（20）第二项中损失函数的系数可统一写成一个关于的函数的形式因此，优化问题（20）可写成：

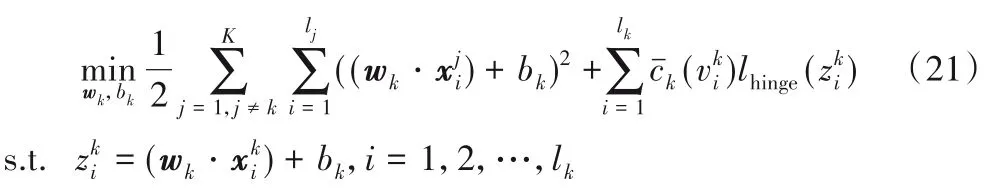
从优化问题（21）看出，与多子支持向量机的优化问题不同之处是惩罚参数是关于的函数，从而给予每个样本不同的惩罚，由此可降低异常值的影响。优化问题（21）的解可通过求解其对偶问题得到。通过引入拉格朗日乘子向量αk，构造拉格朗日函数，利用KKT（Karush-Kuhn-Tucker）条件，可得优化问题（21）的对偶问题［14］：

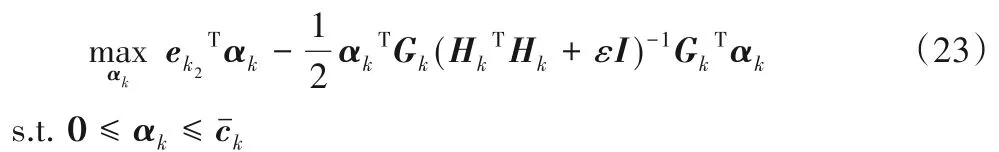
采用变量交替策略求解优化问题（19）的第二步，当得到优化问题（21）的解(wk，bk)时，则优化问题（19）的目标函数第一项为常数，不影响优化问题的解。因此，优化问题（19）等价于：

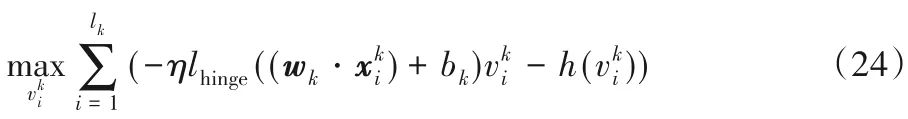
根据共轭函数理论中的式（17）和v 与r的关系式，得到解的关系式由解的关系知式（24）的解析解为：

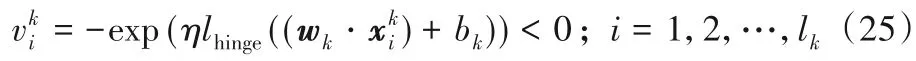
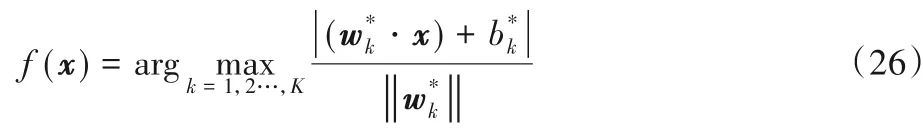
将预测点x代入决策函数，可得相应的类别标签。

综上，归纳线性基于Rescaled Hinge 损失函数的多子支持向量机算法步骤如下：

1）初始化参数。选择合适的参数η ＞0和惩罚参数ck，迭代收敛精度δ。设置s=0和=-1(i=1，2，…，lk)。

2.2 非线性情形

不难想象，很多情况下多类分类问题不能用K 个超平面来构造决策函数，此时可使用核映射将样本点映射到Hilbert空间中，在Hilbert 空间中可实现线性分划，此时在原空间中即是非线性分划。将针对非线性情形，寻找如下带有核函数的K个超曲面：

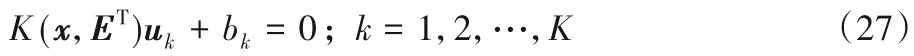
其中E 是由所有样本点构成的矩阵，ET=[A1，A2，…，AK]T，K(⋅，⋅)是核函数。注意到，当核函数被选取为线性核函数时，上述超曲面可退化为超平面。为得到式（27）所示的超曲面，构造如下的优化问题：

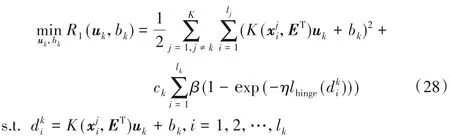
其中ck≥0是惩罚参数。

现在，给出优化问题（28）的求解过程。与线性情形的求解过程相似，用共轭函数理论将优化问题（28）作等价变换。令代入共轭函数理论得到式

（14），则优化问题（28）可用下面的形式表示：

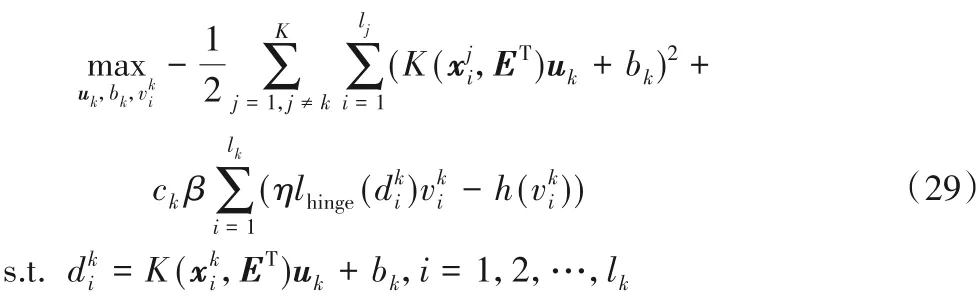
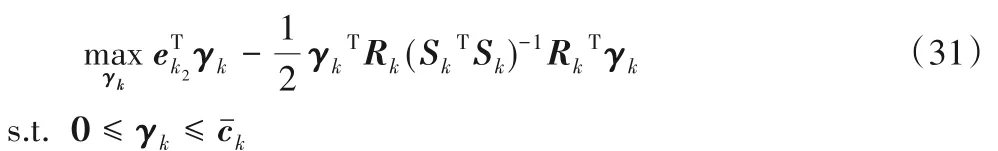
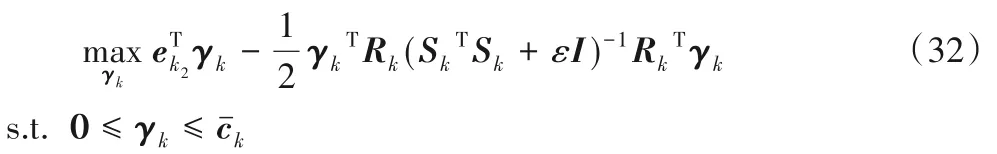
采用变量交替策略求解优化问题（29）的第二步，将(uk，bk)代入优化问题（29）中，可得：

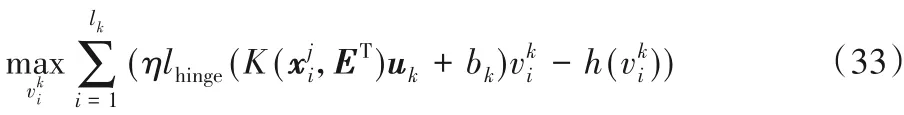
同理，根据共轭函数理论，可知式（33）的解析解为：

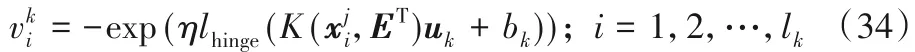
综上，归纳非线性基于Rescaled Hinge 损失函数的多子支持向量机算法步骤如下：

1）初始化参数。选择合适的核函数K(⋅，⋅)，参数η ＞0，核参数p 和惩罚参数ck，迭代收敛精度δ。设置s=0 和

3 数值实验

本章用基于Rescaled Hinge 损失函数的多子支持向量机（RHMBSVM）与多子支持向量机（MBSVM）［14］、基于Rescaled Hinge 损失函数的鲁棒支持向量机（RSVM-RHHQ）［15］进行比较。其中，由于基于Rescaled Hinge损失函数的鲁棒支持向量机只能求解二分类问题，所以本文使用该方法时利用了“一对余”策略解决多分类问题，并在Matlab中编辑其代码。按照多子支持向量机和基于Rescaled Hinge损失函数的多子支持向量机的算法，在Matlab软件中编辑相应的代码。为了方便计算，设参数η ∈{0.2，0.5，1，2，3，4}，惩罚参数c=c1=c2=…=ck选自集合{2-8，2-4，2-1，21，24，28}。选用高斯核函数K(x，x')=其中的参数p 选自集合{1，3，5，7，9}。用五折交叉验证［20］选择参数，并计算各种方法的正确率。实验环境：内存为4.00 GB，64 位的Windows 7 操作系统中用软件Matlab R2016b运行得到。

为了检验本文提出的方法的有效性，在UCI 数据库中选取了6 组数据集，它们分别是：iris、wine、glass、vowel、vehicle、svmguide2。表1给出了6组数据集的详细信息。

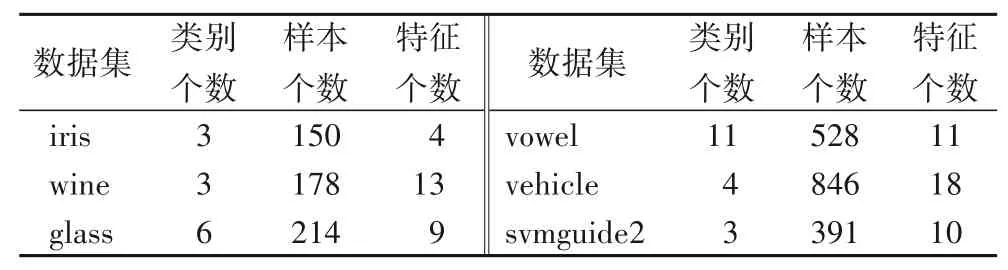
表1 实验中使用的UCI数据集Tab.1 UCI datasets used in the experiment

本文采用正确率（Accuracy，AC）来衡量分类性能。为了表明本文方法性能，针对6 个UCI 数据集进行了实验，并与多子支持向量机和基于Rescaled Hinge 损失函数的鲁棒支持向量机进行了比较，实验结果如表2所示。

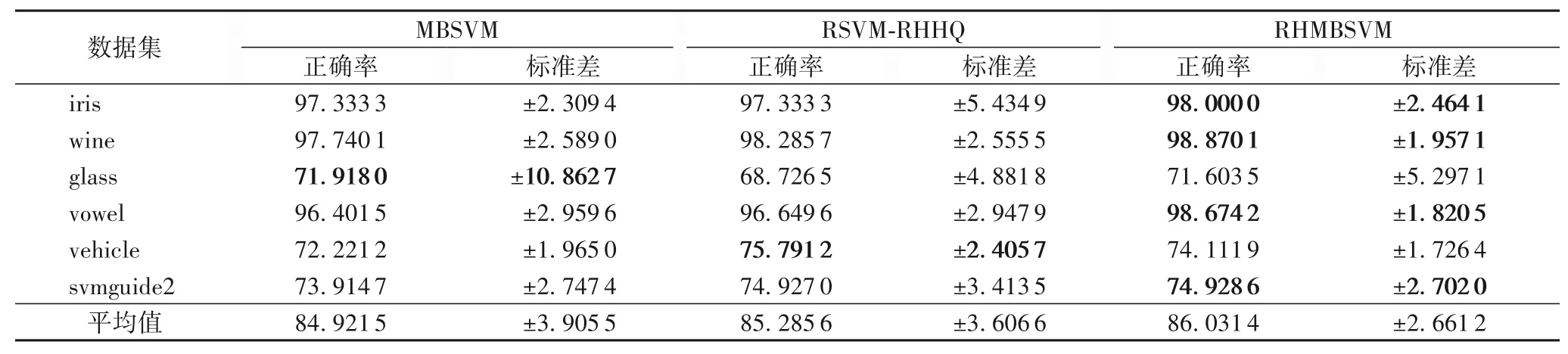
表2 各方法在无噪声数据集上的正确率和标准差 单位：%Tab.2 Accuracy and standard deviation of different methods on noise-free datasets unit：%

表2中对最高正确率进行加粗，由表2可看出本文方法在6个数据集中有4个数据集的正确率都比对比方法高，并且本文的方法对于数据集glass 和vehicle 计算的正确率也和对比方法的结果差不多。从表2 的最后一行可以看出，在对不加噪声的UCI数据集的数值实验中，本文方法正确率比MBSVM平均提升1.11个百分点，比RSVM-RHHQ 平均提升0.74个百分点。因此，表明本文方法比现有的两种多分类方法具有更高的正确率。

为了表明基于Rescaled Hinge 损失函数的多子支持向量机的鲁棒性，分别选取6 个UCI 数据集25%或50%的特征，加入均值为0，方差为0.01 或0.05 的高斯白噪声，并与多子支持向量机和基于Rescaled Hinge 损失函数的鲁棒支持向量机进行比较，实验结果如表3所示。

由表3 可看出，加入不同的噪声，本文方法的性能优于多子支持向量机和基于Rescaled Hinge 损失函数的鲁棒支持向量机，且噪声对算法的影响较小。从标准差可知，本文方法的结果更稳定。从表3 中各方法计算的平均值可看出，在对加噪声UCI数据集的数值实验中，本文方法正确率比MBSVM 提升2.10 个百分点，比RSVM-RHHQ 提升1.47 个百分点，体现出本文方法与其他两种多分类方法相比，对有噪声的数据集具有更好的鲁棒性。

分类的结果与参数的选择有很大的关系，图2 展示了本文 方法 在 参数c ∈{2-8，2-4，2-1，21，24，28}和p ∈{1，3，5，7，9}时，分别绘制正确率的三维柱状图，柱状图中的每一个都是由一对参数c和p确定。

如图2 所示，在所有数据集中，对参数c 和p 的变化敏感度最低的是wine数据集，敏感度较高的有vehicle和svmguide2数据集。在选择参数时，可看出这六个数据集中的大部分数据集选择的参数在p=1，c=21。

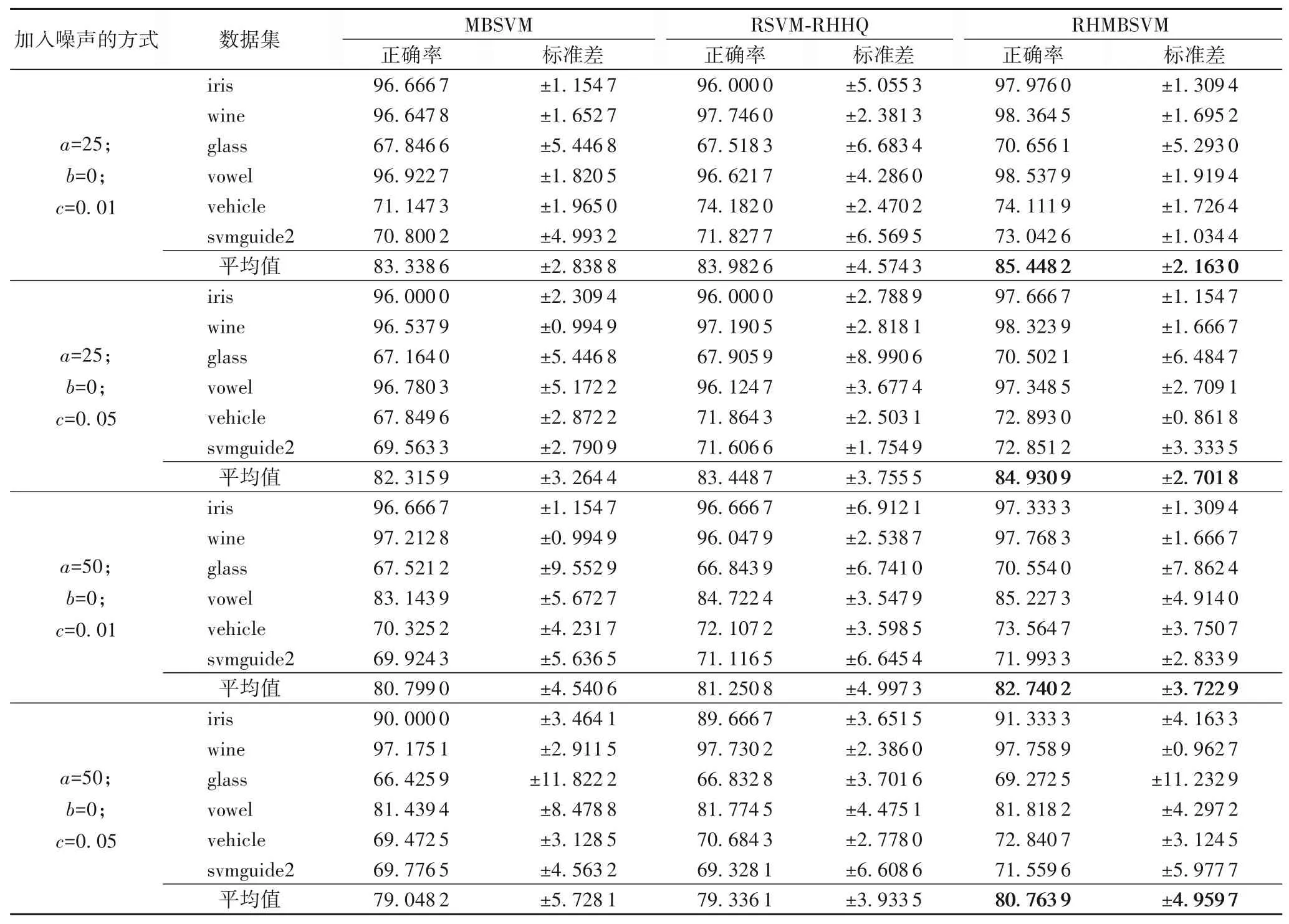
表3 各方法在有噪声数据集上的正确率和标准差 单位：%Tab.3 Accuracy and standard deviation of different methods on datasets with noise unit：%

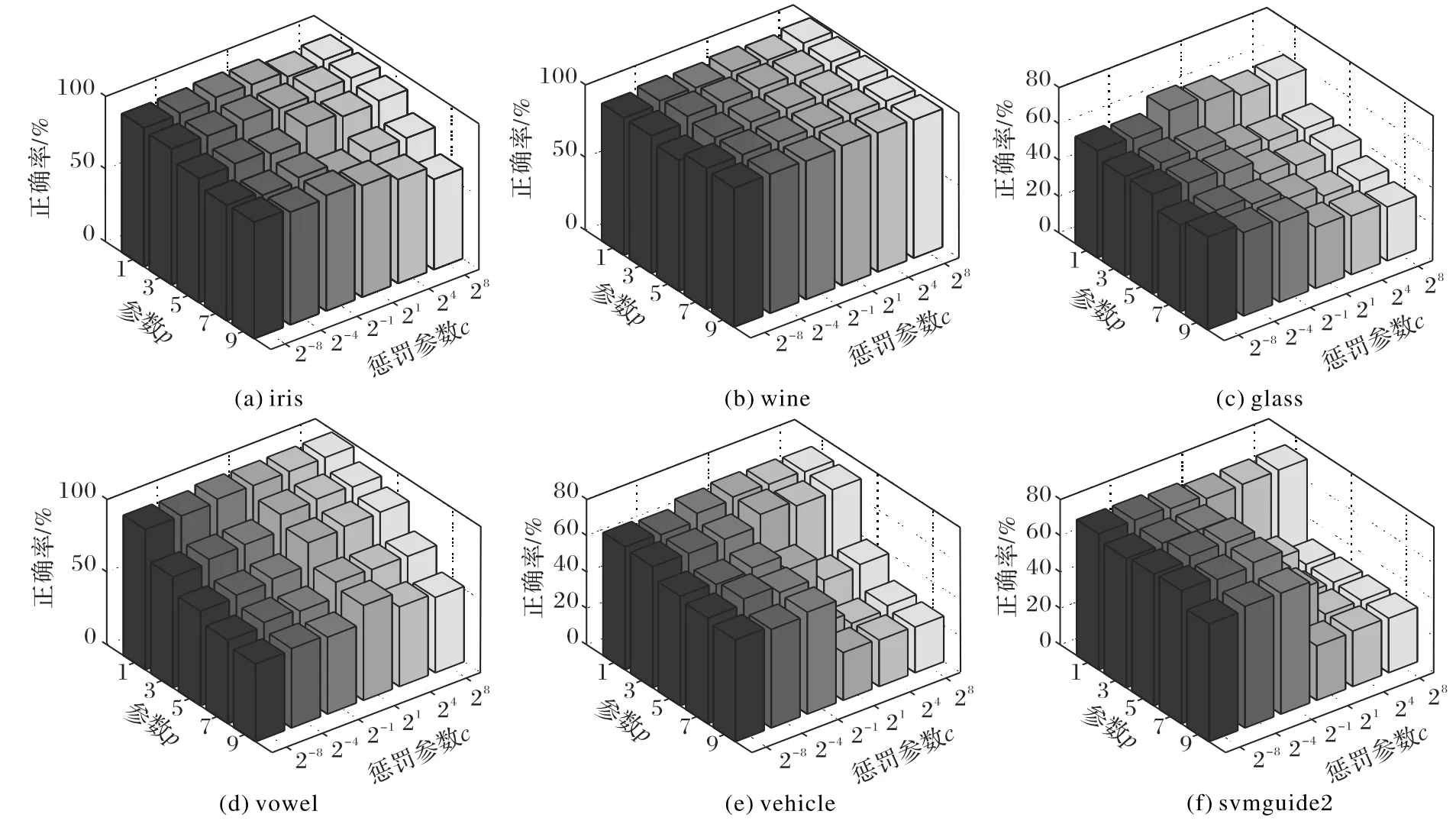
图2 在参数c和p不同值时，RHMBSVM在UCI数据集上的正确率Fig.2 Accuracy of RHMBSVM on UCI datasets with different values of parameters c and p

4 结语

在本文中，对多分类问题中存在异常值这一现象，本文将Rescaled Hinge 损失函数引入传统的多子支持向量机中，提出了基于Rescaled Hinge 损失函数的多子支持向量机。在求解过程中发现，本文方法实际上是一个加权的多子支持向量机，给每个点不同的惩罚，使异常值对决策函数产生更小的影响。本文方法只需求解K 个小规模的二次规划问题，有相对低的计算复杂度。对UCI 数据集进行了实验，并与多子支持向量机和基于Rescaled Hinge损失函数的鲁棒支持向量机的“一对余”策略进行了实验比较，表明了在多子支持向量机中，引入Rescaled Hinge 损失函数，进一步提高了算法的准确性和鲁棒性。接下来可以探索如何降低异常值对支持向量机推广到多分类算法的影响，并且文中参数较多，也可对参数的分析和选择进行更深入探究。