演化信息协助的动态协同随机漂移粒子群优化算法

赵 吉，程 成

（1.无锡环境科学与工程研究中心，江苏无锡 214153；2.江南大学物联网工程学院，江苏无锡 214122；3.中国船舶科学研究中心，江苏无锡 214082）

（∗通信作者电子邮箱queenji97@hotmail.com）

0 引言

随着科学技术的发展，许多现实世界中的优化问题变得越来越复杂，迫切需要更好、更有效的优化算法。粒子群优化（Particle Swarm Optimization，PSO）算法［1］自1995 年首次提出以来，学者们对提高其性能进行了许多尝试［2］。然而，就PSO本身而言，它并不是一种全局优化算法［3］。为此，Sun 等［4］根据外部电场中金属导体的自由电子模型［5］提出了一种新的随机漂移粒子群优化（Random Drift PSO，RDPSO）算法，并且能更加高效地估计复杂生化动力系统的参数。RDPSO 能保持群体的多样性，利用平均位置的等待机制提高粒子的全局搜索能力，比PSO 和遗传算法（Genetic Algorithm，GA）具有更好的性能［6］。RDPSO 算法也可以用作数据挖掘中的优化问题的通用工具，例如聚类、分类、回归等，其广泛存在于现实世界的优化问题［7-8］中。

与其他进化算法一样，RDPSO 算法也面临着早熟收敛和陷入局部最优的问题，导致性能损失和次优解。非重复访问策略与智能进化算法相结合［9-14］，通过使用二维空间分割树避免估计候选解被重复访问，引导算法搜索方向趋于有希望的搜索区域，从而提升搜索能力以提高算法的性能。文献［14］提出了基于搜索历史信息的非重复访问量子行为粒子群优化（Non-revisited Quantum-behaved PSO，NrQPSO）算法，利用搜索历史记录访问过的解位置，有效提高算法性能。但是其变异方式采用了简单的单粒子随机翻转变异，没有充分利用群体中粒子间的信息传递。同时NrQPSO 需要设置参数阈值e，该值是个经验值，对解的影响很大，需要多次调试才能达到最优值，因此算法性能对该值的依赖度较大，不具备普遍性。为了进一步提高RDPSO 算法在复杂优化问题中的性能，提高粒子的多样性，本文提出演化信息协助的动态协同随机漂移粒子群优化（Cooperative RDPSO，CRDPSO）算法，粒子动态地进行协同合作，通过演化过程中的信息协助同时记录访问过的解位置和适应度值，避免算法重复访问，增强自适应变异从而显著提高收敛精度和速度。

1 随机漂移粒子群优化算法

给定一个最小优化问题：

其中F(X)是一个在连续可行空间S 中的适应度函数（或目标函数）。假设在具有m个粒子的群优化算法中，每个个体都被视为D 维空间中的无体积粒子，第k 代第i 个粒子的位置向量和速度向量分别表示为：以及粒子的个体最优位置（personal best，pbest）（给出最佳目标函数值或适应值的位置）。群体有一个称为全局最佳（global best，gbest）位置的向量它定义为种群中所有粒子中最佳粒子的位置。根据式（1）分别按式（2）和式（3）计算：

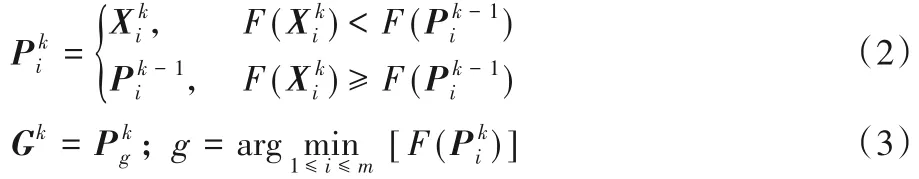
轨迹分析［15］表明，假设每个粒子都收敛到其局部吸引子，粒子群优化算法的收敛性是可以实现的。在PSO 算法中，粒子向个体最优位置的方向运动类似于外部电场中金属导体内电子的漂移运动。然而，根据自由电子模型［5］，除了电场引起的定向运动外，电子还处于随机性的热运动中。电子运动的总体效应是电子倾向最小势能的位置。因此，如果把电子的位置作为问题的候选解，势能函数作为问题的目标函数，电子的运动显然与求最小解的过程非常相似。受此启发，假设PSO 中的粒子像是在外部电场中金属导体内移动的电子，粒子的运动是热运动和指向粒子个体最优值方向运动的叠加。因此，粒子的速度可以表示为：其 中分别表示热运动和定向运动的速度。基于这样的假设，文献［4］提出了下列RDPSO粒子更新方程：

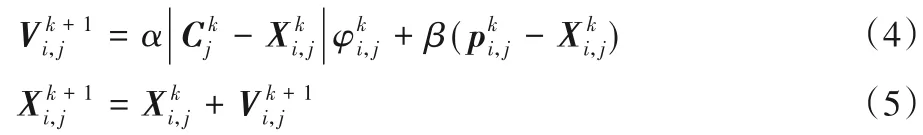
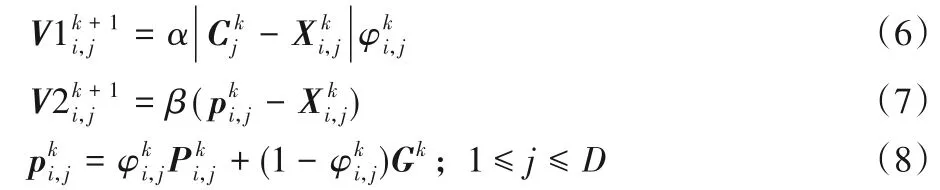
2 演化信息协助的CRDPSO算法

2.1 动态协同机制

对于高维问题，包含随机算法（如随机漂移粒子群算法和遗传算法等）在内的搜索算法都存在尺度规模的“维数灾难”问题。协同机制的重要性在于，它能使粒子群中粒子“好”的维度信息得以保留，并能防止丢弃潜在的有用信息。粒子的每个维度通过执行协同操作，可以分别评估每个维度的优劣，并保存最有用的信息加速收敛。协同进化机制可以提高算法在高维问题中的性能［17-18］。在进化的每次迭代中，每个粒子都会动态地连续更新一个上下文粒子向量，以便在协同合作过程的每个连续阶段获得新的信息。为了减少每个维度替换的适应度函数计算量，通过选择最优粒子向量并与其他粒子协作。改进的动态协同进化方式，进一步提高动态协作性能。在进化过程中，每个粒子xi通过进化公式产生5个进化的粒子｛xi_1，xi_2，…，xi_5｝。因此，连同xi共得到6个个体，根据式（1）分别计算其适应度值，在6 个个体中选择最佳个体xi_b；然后将xi_b指定为粒子xi的当前较优局部上下文粒子向量，随后将xi_b与其余5 个个体进行协同进化。对于xi_b向量的每个维度，分别用其他5 个个体的对应维度替换，并测试替换维度是否提高了适应度值。如果是，则采用替换值，并使用结果向量替换上下文粒子向量。重复此过程，直到所有5 个测量向量的所有维度都得到评估，并选择最佳排列以形成新一代的粒子。动态协同进化机制的过程算法描述如下。

步骤1 对于当前粒子xi根据RDPSO 进化式（4）、（5）、（8）进化产生5个子代粒子｛xi_1，xi_2，…，xi_5｝。

步骤2 从｛xi，xi_1，xi_2，…，xi_5｝中选取最优的粒子作为动态协作的上下文粒子向量xi_b。

步骤3 对于剩下的5个粒子，分别对每个粒子的每一个维度用xi_b的相应维度替换，同时根据式（1）计算适应度值，如果替换后的粒子适应度值优于F（xi_b）则保留相应维度，否则保留原有维度值。

步骤4 直到所有剩余5 个粒子都和上下文粒子向量比较完，保留具有最优适应度值的粒子作为本次粒子进化的子代粒子。

步骤5 返回步骤1 直到粒子群所有粒子都进行了动态协同进化后产生新的子代粒子群。

2.2 基于演化信息的自适应变异

CRDPSO 使用二维空间分割（Binary Space Partitioning，BSP）树作为演化历史信息的存储方式，其记录了每个粒子的位置和适应度值｛［xi，F（xi）］｝，根据｛xi｝的分布将整个搜索空间S 进行划分。最初，CRDPSO 中的BSP 树T 仅包含根节点。树的每个节点记录了RDPSO 先前访问的不同解xi。同时，它还记录了搜索空间的子区域Si。节点使用欧几里得度量来对搜索空间进行二维分割。两个子节点a 和b 子节点沿着第k维将父节点的子区域线性分割为两个重叠的子区域，k的选取满足a 和b 在k 维上的距离最大，即arg max|a(k) -b(k)|。假设｛x1，x2，x3，x4，x5｝是二维搜索空间内的估计解，它们在二维平面空间的分布如图1（b）所示。记录估计解的BSP树结构如图1（a）所示，BSP 树根据估计解将二维搜索空间划分为多个小区域，如图1（b）的虚线区域所示，每个区域对应于现有的解。每个树节点包含其关联解的各种搜索演化信息（包括搜索空间中的解位置、适应度值等）及其在搜索空间分配的子区域。以这种方式，RDPSO 生成的每个历史解被记录在树的节点中，并且BSP树用作查询xi子区域的有效数据结构［11］。

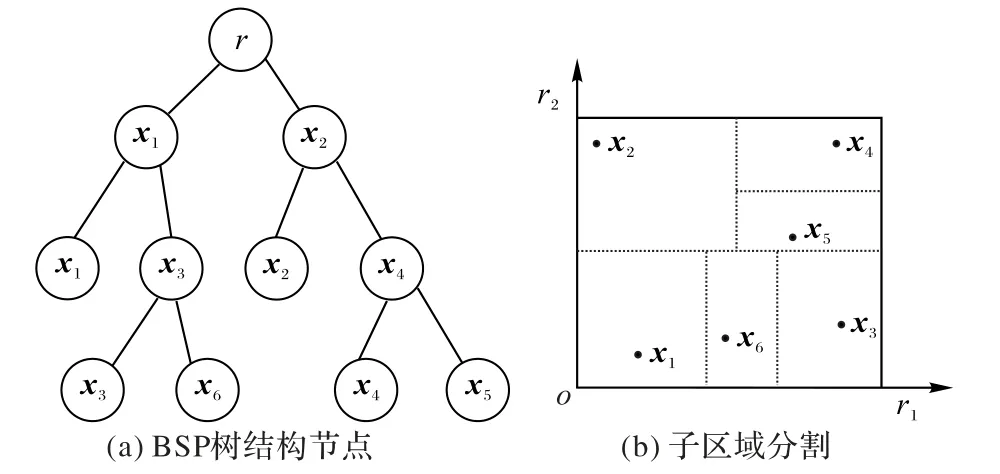
图1 BSP树结构实例Fig.1 Example of BSP tree structure

因为BSP 树同时记录了所有解的适应度值F（xi），该记录可以看作适应度值F（x）的近似值如果解xk的子区域是Sk，一个候选解x 在子区域Sk内，那么解x 的适应度值可以近似为xk的适应度值，即通过标准树节点插入操作来实现，其近似误差随着BSP 树中一个一个记录的解数量增加而单调减小。本文采用的基于梯度下降式的变异方式是一种自适应的、无参数和引导的变异操作。其基于整个搜索历史自适应地调整变异步长，其搜索方向由近似适应度值控制，而不是像单粒子随机翻转突变那样随机。假设X 和Y 分别是节点x和y的子区域，如果X⊆Y，则Y 是X 的邻居。与X 相关的Y 的邻居数量为节点x 和y 的深度差。因此，首先找到子区域X 的最优值，即节点x 的适应度值是其子区域邻居中最佳值，那么其所在子区域可以看作是其邻居子区域的最优子区域。引导自适应变异被定义为指向其最近的最优子区域方向，其变异方向就是向着离近似适应值F˜(x)局部增长最大的方向移动。设置一个变异方向变量W作为指向x 的最近历史最优y 的方向，即W=y -x。近似适应度值被看作一个阶跃函数，因此其最优值的形式是一个D 维子区域而不是一个点。因为BSP树记录适应度值的拓扑结构代表了子区域之间的邻接关系，因此找到离x 最近的最优值相当于在中寻找x的最近最优子区域。为了平衡梯度下降方向分配的搜索效果，引入区间（0，1）内的随机值作为变异步长α。因此x变异公式为：

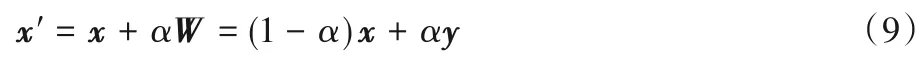
如果x 就是局部最优，即x=y，那么将从x 的子区域中随机选择一个突变体xm。图2 显示了自适应变异的示例，搜索空间S 和个体序列（即BSP 树）空间分割和图1 一样。假设x是要变异的个体，相应的变异从搜索x 子区域开始，在实际编程中是从根节点开始。假设搜索终止于节点x5，S2是x的子区域，然后计算S2到所有最优子区域的距离，其最近的最优子区域是S5。因此，x 的变异范围是位于x 和x5之间直线上的一个点。变异操作步骤如下：

步骤1 搜索待变异粒子x的子区域s ⊆S。

步骤2 找到子区域s的最近最优子区域。

步骤3 y是子区域s中的估计解。

步骤4 如果x=y，x 在子区域内进行随机变异，xm=Random（s）；否则xm=(1-α)x+αy（变异步长在自适应调整范围内随机分配，α=Random(0，1)。

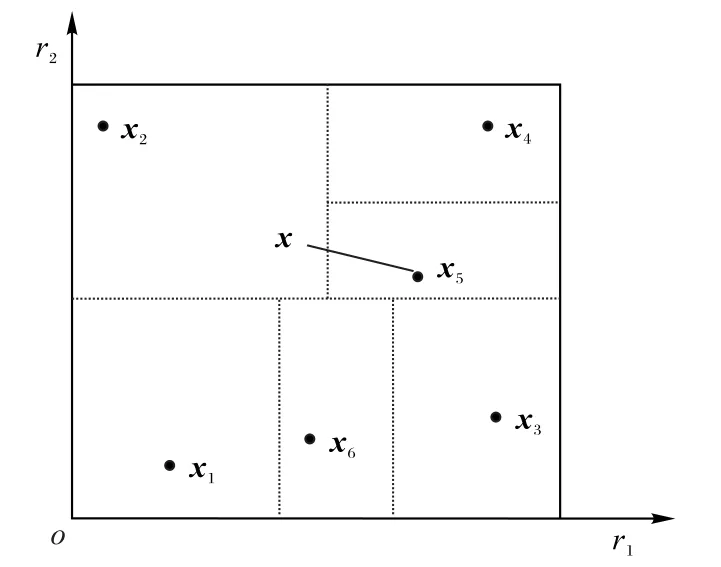
图2 自适应变异（x和x5之间的直线是x变异的可能范围）Fig.2 Adaptive mutation（straight line between x and x5 is the range of possible mutation range of x）

2.3 演化信息协助的动态协同随机漂移粒子群优化算法

本文提出的CRDPSO 可以看作是RDPSO 算法模块和自适应变异模块的结合体，其中算法模块包含了动态协同进化的随机漂移粒子群优化算法，而自适应模块则是由历史信息记录和随机梯度下降式自变异操作组成，如图3 所示。对于一个D 维搜索空间S⊂RD，算法中的单个粒子x 是一个1×D 的实值向量，即x ∈RD。算法通过4 个主要步骤来搜索最优值，即种群初始化、搜索、变异和进化，其重点是通过演化历史信息，动态协同进化的自适应变异来增强种群多样性。CRDPSO 从初始化粒子群P=｛xi｝开始，同时BSP 树初始化为只包含根节点的树T，记录每个粒子的位置和适应度值。之后，粒子群经过自适应变异操作产生粒子群。随后根据动态协同机制，选择最好的置换粒子形成子代粒子群。产生新的粒子群子代后需要重新计算粒子的适应度值并连同位置一起插入树T中，重复算法直到迭代次数超过预定值为止。

图3 显示了CPDRSO 算法的流程，数字表示CPDRSO 迭代中的步骤顺序。

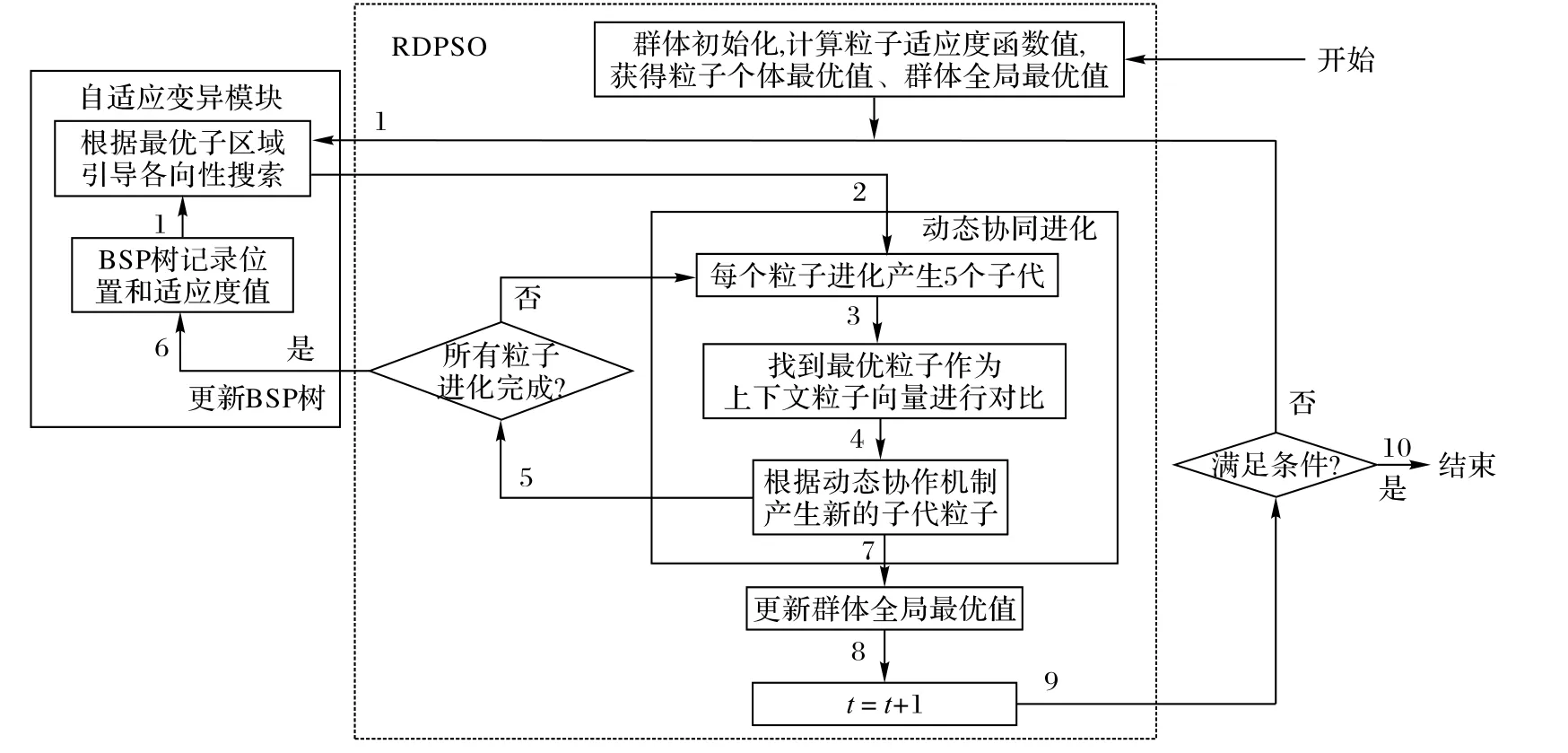
图3 CRDPSO算法流程Fig.3 Flowchart of CRDPSO algorithm

3 测试及结果

3.1 测试函数

本文采用一组标准测试函数包括多峰或单峰基准函数F=｛f1（x），f2（x），…，f10（x）｝［19-20］来测试所提出的算法并验证其性能，表1中显示了10个测试函数，所有的仿真研究都是在Matlab中进行的。

表1 测试函数Tab.1 Test functions

3.2 算法设置

除了RDPSO 和CRDPSO 算法，差分进化算法（Differential Evolution，DE）［21］、协方差矩阵适应进化策略算法（Covariance Matrix Adaptation Evolutionary Strategy，CMA-ES）［22］、非重复访问遗传算法（Continuous Non-revisiting Genetic Algorithm，cNrGA）［11］和三种版本的QPSO，即CCQPSO（Cooperative Quantum-behaved PSO）［18］、CLQPSO（Comprehensive Learning Quantum-behaved PSO）［23］和NrQPSO［14］也通过测试函数进行性能比较。在实验中，CRDPSO 和RDPSO 的参数设置与文献［4］中推荐的参数相同。对于CLQPSO，β 从1 线性下降到0.5，其他因子设置同文献［23］；NrQPSO设置同文献［14］。对于cNrGA，交叉速率是均匀交叉，设置为rx=0.5。对于所有比较的算法，群体大小设置为100，最大迭代次数设置为2 000。所有测试函数的维数设置为D=30。每种算法在实验中独立运行30 次，测试结果取值为30 次独立实验获得最优解的最好，最差和平均值以及标准偏差。

3.3 结果分析

对于所有测试函数，表2 中列出了每种算法30 次独立运行2 000 次迭代的统计值，其中“Best”“Worst”和“Ave.”，分别代表30 次独立运行中获得的最优解的最好值、最差值以及最优解的平均值，“Std.”代表获得的最优解平均值的标准偏差。黑体字的值意味着对应算法对于特定测试函数是测试算法中最优的。从表2 可以清楚地看到，对于所有测试函数，本文提出的CRDPSO 算法性能都优于其他七种算法。虽然RDPSO和CCQPSO在f1、f2和f6上均表现了出色的性能，但CRDPSO算法在所有其他测试函数上均胜过它们。除f9以外，CRDPSO算法的标准偏差对于几乎所有测试函数都是最优的。这表明CRDPSO 对于绝大多数测试函数都能获得最优解，具有最好的算法稳定性。此外，详细的仿真结果（“Best”“Worst”“Ave.”和“Std.”）表明，CRDPSO 的性能表现在十种测试情况下均排名第一。因此表2中列出的仿真结果表明，CRDPSO的整体性能优于其他比较的算法。通过使用演化信息机制，CRDPSO 可以确保搜索过程中的非重复访问以及快速收敛到局部最优。同时，它利用自适应突变来指导粒子搜索更好的邻域，进一步提高局部搜索能力，使得CRDPSO 算法可以获得最好的平均最优值，并且也是最稳定的。

不同算法的收敛曲线如图4所示。

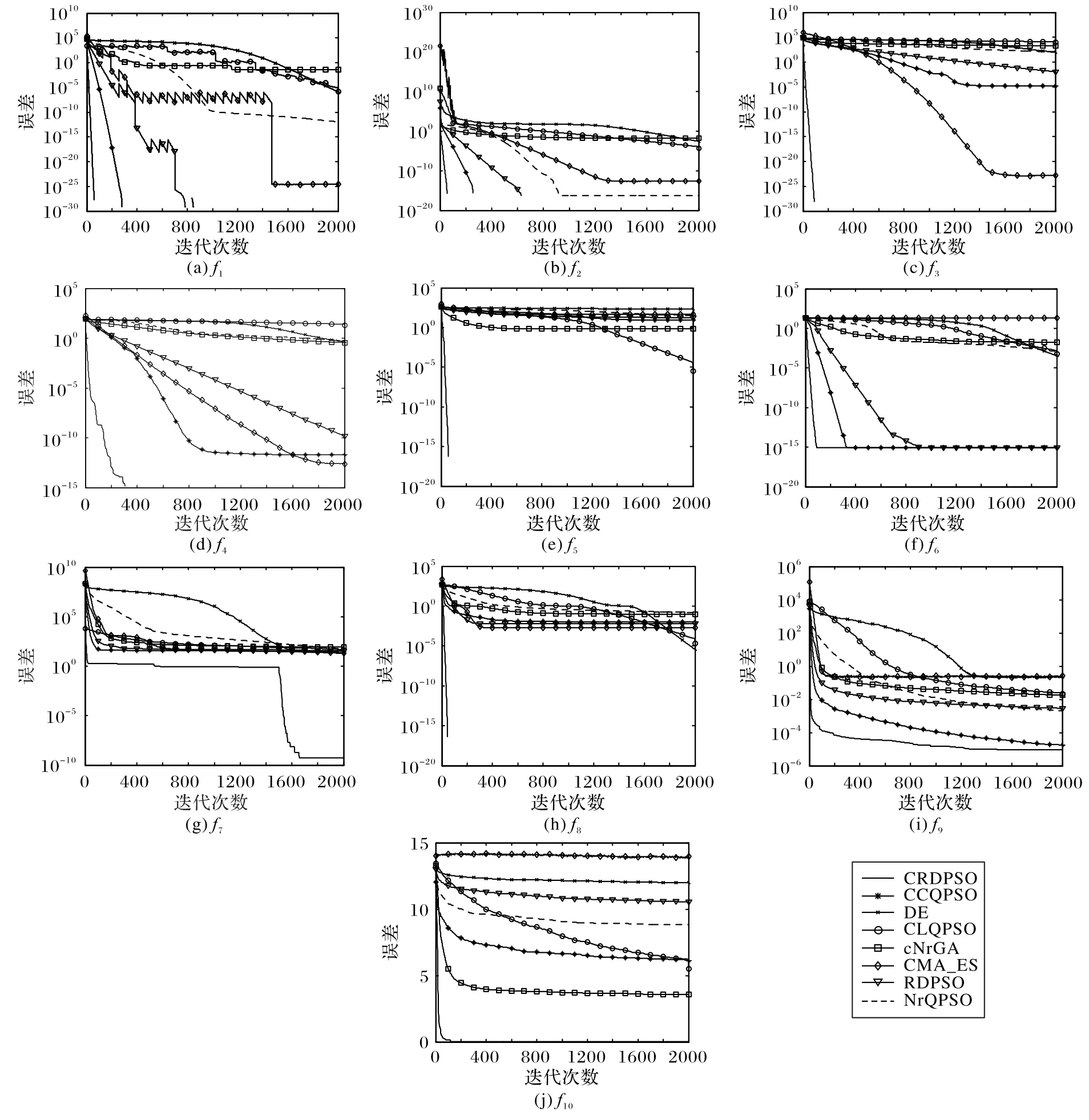
图4 不同算法的收敛曲线Fig.4 Convergence curves of different algorithms

表2 结果表明，对于f1、f2和f6，RDPSO、CRDPSO 和CCQPSO 算法最终都达到了最优值。然而，从图4（a）、（b）、（f）的收敛曲线可以看出，CRDPSO 的收敛速度远优于其他两种算法，在不到200 次的搜索迭代中，它就已经能收敛到全局最优值。对于f3～f5和f7～f10，CRDPSO 的收敛速度和收敛精度也远远超过其他七种算法，在很短的迭代次数内就找到了每个测试函数的全局最优值。CRDPSO 算法能够更快地搜索到最优值是因为粒子一旦利用整个演化历史信息找到自己最近的最优邻域子区域，就可以进行自适应变异；同时，利用动态协同机制保持最优信息，使算法能够快速收敛到全局最优值。在图4中，对于f1～f5和f8，CRDPSO已经达到Matlab能够识别的0，并且0 的对数比例是负无穷大，因此适应度值不能再在图中显示。这很好地说明，对于这些测试函数，CRDPSO 获得的目标函数值的仿真结果无限接近理论值，即0。对于图4（g）中的f7，即使CRDPSO 算法已经趋于收敛，但在后期（即1 500次迭代后）还能够进一步找到一个新的更好的解，这说明CRDPSO 算法在搜索过程的最后阶段仍然具有更好的搜索能力，并且有很大的机会逃离局部最优解而得到更好的解。综上所述，CRDPSO 算法与其他算法相比，具有最佳的收敛性能和优化精度。

为了确定除精度和收敛性外，CRDPSO 算法与其他七种算法之间的性能是否存在显著差异，表3 列出了不同算法之间的显著性水平为0.05的Wilcoxon秩和检验结果。从表3中可以看出，对于f1、f2和f6，CRDPSO，RDPSO 和CCQPSO 没有显著差异。然而，对于绝大多数测试函数，CRDPSO 算法可以得到h=1，这表明与其他算法相比，CRDPSO 的优化性能有了显著提高。结果表明，无论是在单峰函数还是多峰函数中，CRDPSO 算法的最优性能都明显较高，收敛更快、最优值精度更高。

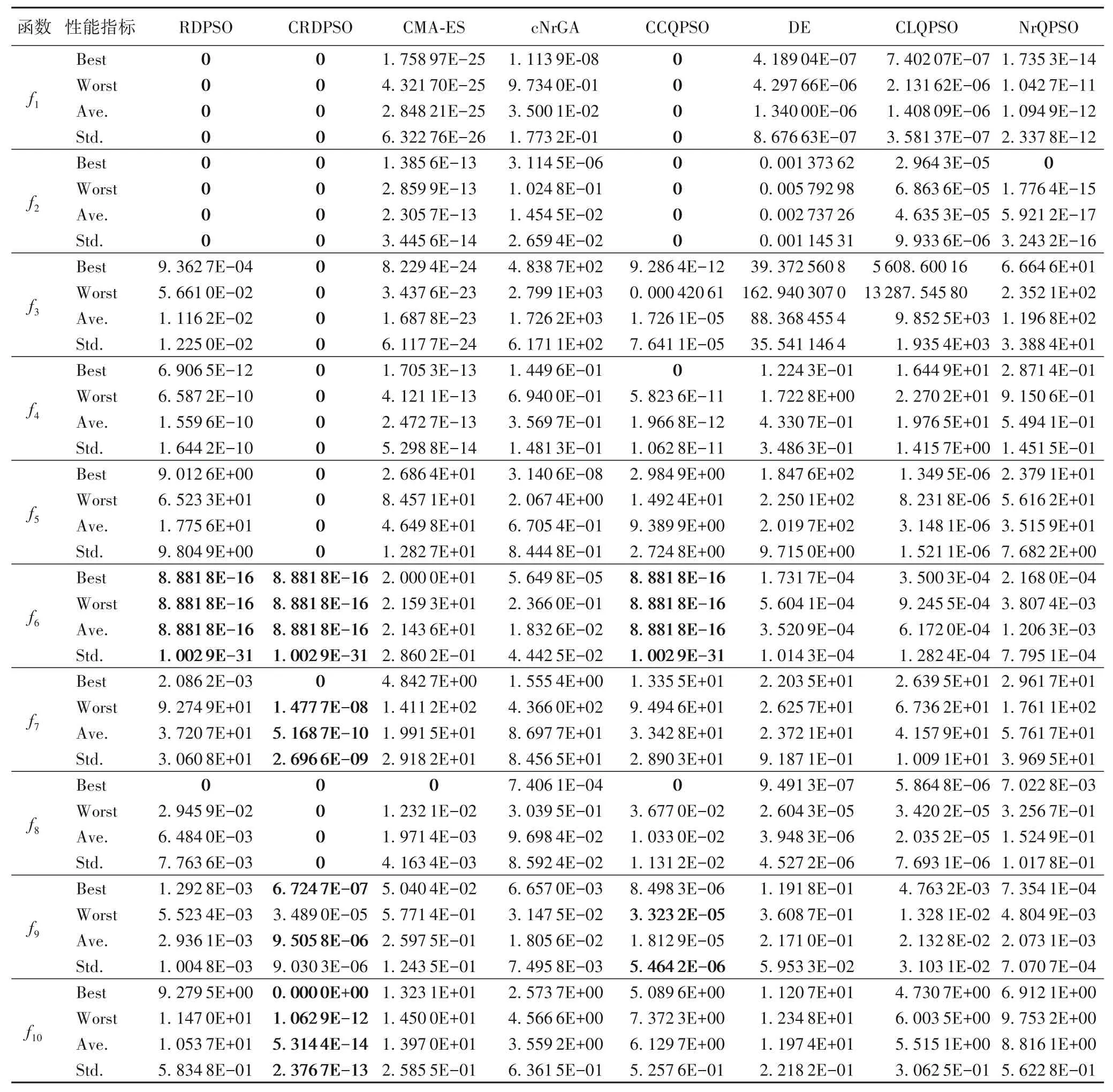
表2 测试函数仿真结果Tab.2 Simulation results of test functions

进化算法运行时间主要耗费在生成解和适应度函数计算。不同算法采用不同的策略生成可能解，CRSPSO 的群体多样性保持比较好，因此目标函数收敛较快，主要运算时间在于访问BSP 树（即搜索和插入节点）和动态协作的适应度计算。对比cNrGA 和NrQPSO，由于CRDPSO 还需要进行额外的动态协同计算，因此花费的时间也会相应增加，但是CRDPSO获得的解精度比cNrGA 和NrQPSO 有大幅提高。CRDPSO 和CCQPSO算法都具备协同操作。CRDPSO每次迭代时，每个粒子都需要和动态上下文粒子向量进行对比获取更好的适应度值从而增加了计算开销。CRDPSO 又利用了搜索历史信息，因此比CCQPSO 提高了整体收敛速度并进一步提高了准确度。总体而言，CRDPSO 算法增加时间和空间成本提升精确度和收敛度性能，这也充分符合了没有免费午餐的理论。对于实际问题如表面配准、加热优化设计和能源管理、通风和空调系统等，适应度函数评价需要比解生成耗费更多的时间。根据目前电脑硬件的发展，对于这类实际应用问题，CRDPSO所需要的额外时间开销和建立BSP树所需要的容量对于提高算法性能都是可以接受的，其综合性能是可以适应的。

表3 Wilcoxon秩和检验结果Tab.3 Wilcoxon rank sum test results

4 结语

在RDPSO 算法中，早熟收敛和粒子多样性是急需解决的两个问题。为此，本文提出了演化信息协助的动态协同RDPSO 算法（CRDPSO），将动态协作机制与标准RDPSO 算法相结合。群体粒子之间的动态协作机制采用动态上下文粒子信息可以更好地利用任何新的信息，增强了群体的搜索能力，有助于防止算法的早熟收敛。该算法通过搜索历史信息方案，利用二维空间分割（BSP）树结构来存储估计解的位置和适应度值。受益于空间划分方案，使用的记录树结构获得一种用于改进CRDPSO 中突变策略的快速适应度函数，由此产生无参数的自适应变异，从而提高了粒子的变异能力。与其他比较流行的搜索随机算法相比，对于10 个标准测试函数上的实验结果表明，该算法具有最好的全局寻优能力，并且收敛速度和精度都有所提高，证明了CRDPSO 的有效性和高效率。改进后的算法在理论上可以证明其优越性，但在实际问题中还需要进一步验证。因此，将CRDPSO 算法应用于实际工程问题成为未来的研究重点。下一步研究工作是验证CRDPSO算法在电力经济调度、数据分析和生物路径参数识别等工程应用中的性能。同时，为了进一步充分利用和挖掘有效历史信息，历史演化信息在粒子群搜索中的信息动态可视化也是今后的一个研究内容。