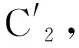将军饮马问题的变式探究

程柳莎

(浙江省东阳市第二高级中学, 322100)

传说古希腊有一位精通数学和物理的学者,名叫海伦．一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题:将军每天骑马从城堡A出发,先到河边饮马,然后再去河岸同侧的城堡B开会,应该怎样走才能使路程最短?据说海伦略加思索就解决了它,从此以后这个被称为将军饮马的问题被广为流传．这实际上是在直线上找一点到两个定点的距离之和的最小值问题．本文以此为基础进行延伸,整理了与此类似的平面内到两个点的距离之和的最值问题,即|PA|+|PB|的最值问题及其求解思路．下面，就三类模型作业具体分析.

模型1二个定点一个动点

当动点只有一个时,可利用两点之间线段最短求出最小值．为了形成三点共线,可以利用动点所在的曲线的轨迹将同侧的两个定点化为异侧的两个定点．

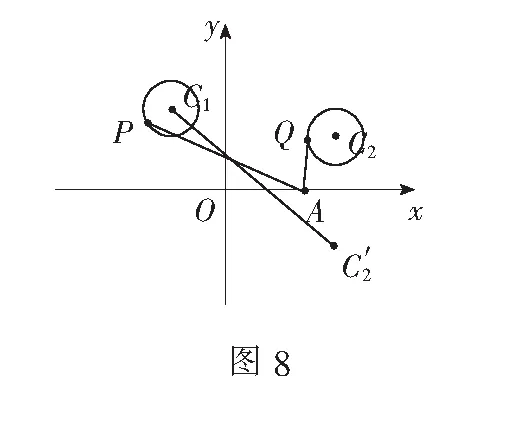
1. 动点在直线上时,利用对称点转化

2. 动点在圆锥曲线上,一个定点为焦点时,利用定义转化

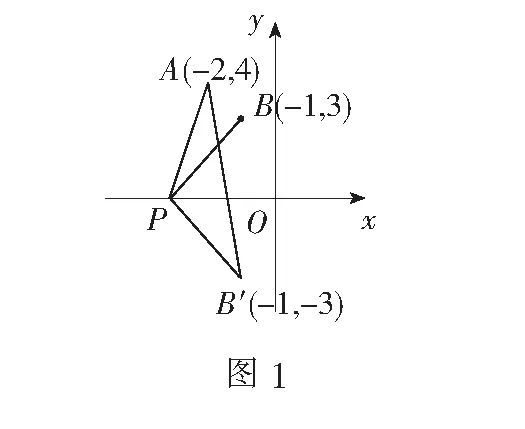
例2已知P为抛物线C:y2=8x上的一个动点,F为抛物线的焦点,点A的坐标为(4,1),求|PA|+|PF|的最小值．

解如图2,过P,A分别作抛物线的准线x=-2的垂线,垂足为H,E.由抛物线的定义可知|PF|=|PH|,于是|PA|+|PF|=|PA|+|PH|≥|AE|=6,所求最小值为6.

评注若动点在抛物线上,一个定点为焦点,另一个定点在抛物线外侧,则定点与焦点的连线段的长即为所求最小值;若一个定点为焦点,另一个定点在抛物线内侧,则此定点到准线的距离即为所求最小值.

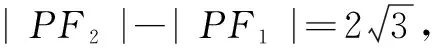
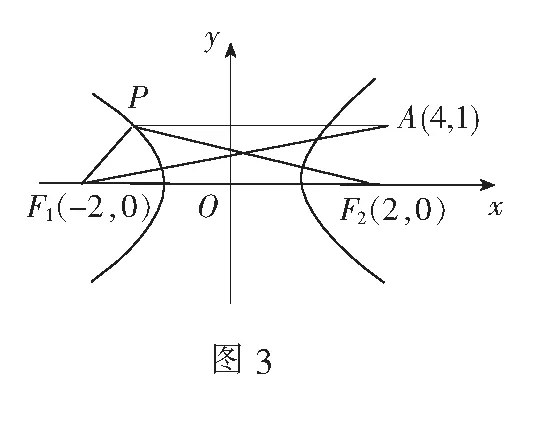
评注若动点在双曲线的左支或右支上,一个定点为焦点,另一个定点与焦点所在双曲线这一支的两侧,则由两定点连线段的长可得最小值;若另一个定点与焦点在动点所在双曲线这一支的同侧,则利用双曲线的定义转化,可求得最小值．

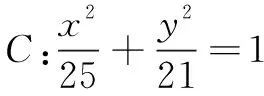
解如图4,易知点A在椭圆内部.由椭圆的定义知|PF2|+|PF1|=10,故|PF2|=10-|PF1|,|PF2|+|PA|=10+|PA|-|PF1|.

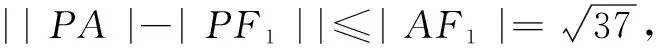
评注若动点在椭圆上,一个定点为焦点,另一个定点在椭圆外侧,则定点与焦点的连线段的长即为最小值,利用椭圆的定义将距离之和转化为距离之差,可求得此定点与另一个焦点的连线段与长轴的和为最大值;若另一个定点在椭圆内侧,类比例4可求得最大值与最小值．

3.动点在圆上时,利用阿波罗尼斯圆的性质(反演点)或椭圆的定义转化

例5若向量a,b满足|a|=1,|b|=2,求|a+b|+2|a-b| 的最小值．

分析1向量的模可表示两点间的距离,所以|a+b|+2|a-b|为距离的线性之和.考虑把系数化为相同的情形,从而将目标函数转化为距离之和,利用阿波罗尼斯圆的反演点求解.

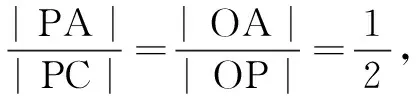
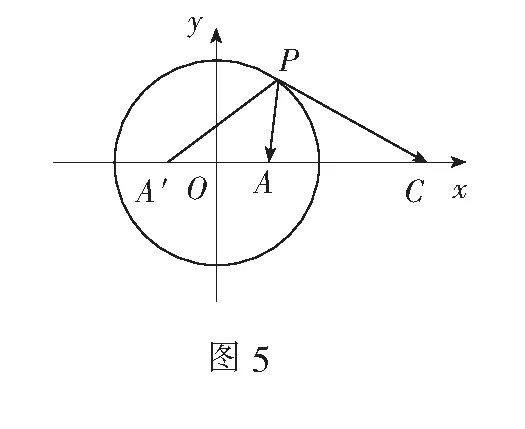
分析2既然能通过求阿波罗尼斯圆的反演点,将线性和化为距离之和,必然可从代数角度直接转化为距离之和．

解法2设点A(1,0),A′(-1,0),C(4,0),P(x,y),a=(1,0),b=(x,y),则有x2+y2=4.于是

|a+b|+2|a-b|

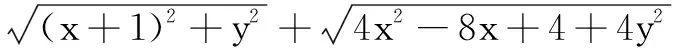
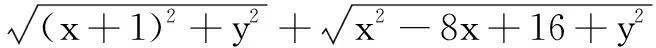
=|PA′|+|PC|

≥|A′C|=5.

例6(2017年浙江高考题)已知向量a,b满足|a|=1,|b|=2,求|a+b|+|a-b|的最小值与最大值．

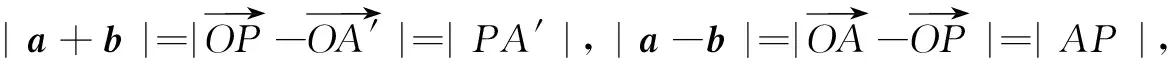
由线段AA′在圆内部,设|PA′|+|PA|=2a(a>1),则点P在以A,A′为焦点、2a为长轴长的动椭圆上.又因为点P也在圆x2+y2=4上,故当动椭圆与圆有公共点时,可求此椭圆长轴的最大和最小值.

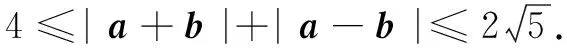
模型2一个定点二个动点

当动点有两个时,可先固定其中一个动点,研究另一个动点对距离之和的影响,然后再看此动点对距离之和的影响,逐一进行突破．

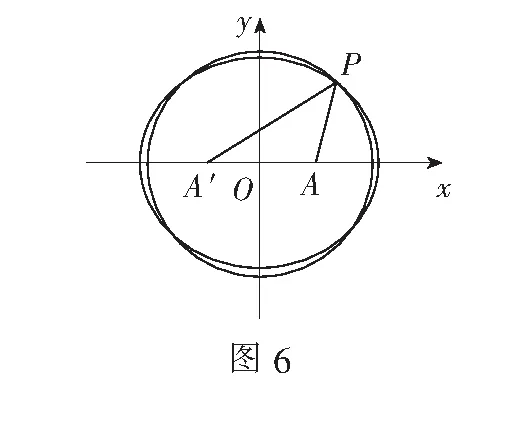
例7已知P为抛物线C:y2=8x上的一个动点,F为抛物线的焦点,动点A在圆D:(x-4)2+(y-1)2=1上,求|PA|+|PF|的最小值．

解如图7,过点P,D分别作抛物线的准线x=-2的垂线,垂足为H,E,由抛物线的定义可知|PF|=|PH|.

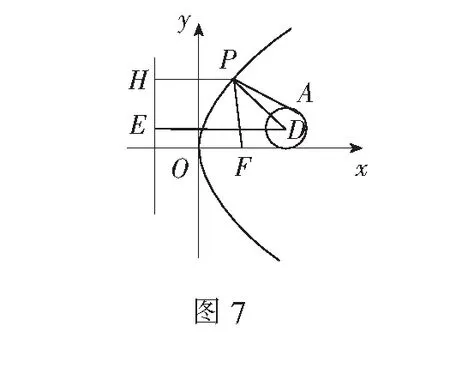
又因为|PA|≥|PD|-1,所以

|PA|+|PF|=|PA|+|PH|

≥|PH|+|PD|-1

≥|DE|=5,

故所求最小值为5.

模型3三个动点

当动点有三个时,可先固定其中两个动点,研究第三个动点对距离之和的影响;然后再看第二个动点对距离之和的影响,以此类推逐一进行突破．

例8已知点P,Q分别为圆C1:(x+2)2+(y-3)2=1及圆C2:(x-4)2+(y-2)2=1上的动点,动点A在x轴上,求|PA|+|QA|的最小值．

解先固定点P,Q,视点A为动点,则|AP|≥|AC1|-1,|AQ|≥|AC2|-1,得|PA|+|QA|≥|AC1|+|AC2|-2．