对一道竞赛题的探究
郑国岐 郑颖欣
(湖北省沙市第五中学,434000) (湖北省沙市中学,434000)
一、试题呈现
(2020年浙江省数学夏令营赛题)将1~2 020的数字按顺时针方向围成一个圆圈(如图1),然后从1开始,按顺时针方向依次隔一个数拿走,即拿走数字1,3,5,…,这个过程一直进行下去,直到剩下最后一个数字,则最后剩下的数字是多少?(注:内圈数字表示所有数字排列的序号,外圈数字表示依次拿走的序号)
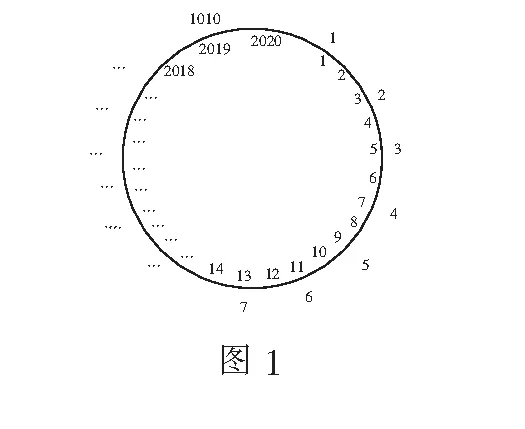
二、规律探寻
我们从简单到复杂依次进行探究,看其中是否隐藏着某种规律?
第一步:人数n依次是2,3时,如图2依次求得最后剩余的数字编号m.如下表:

n23 m22
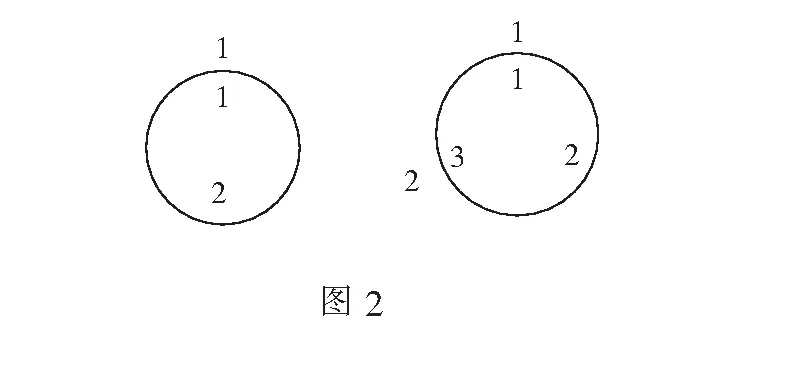
第二步:人数n依次是4,5,6,7时,如图3依次求得最后剩余的数字编号m.如下表:
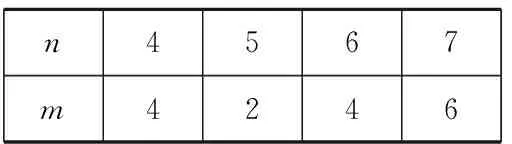
n4567 m4246
第三步:人数n依次是8,9,10,…,15时,依次求得最后剩余的数字编号m.如下表:

n89101112131415 m82468101214
第四步:人数n依次是16,17,18,…时,依次求得最后剩余的数字编号m.如下表:
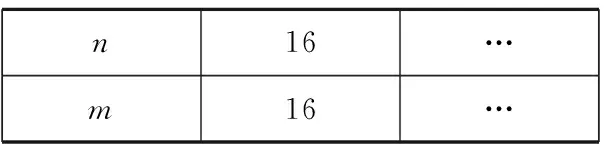
n16… m16…
由此猜想:

n2n2n+12n+2…2n+k(k<2n)m2n24…2k
三、证明猜想
命题1将数列1,2,3,…,2n(n≥1)的数字顺时针围成一个环,从去掉1开始,然后按顺时针方向隔一项再去掉一个数,…,依次进行下去,最后剩余的数为2n.
证明当n=1时,最后剩余的数是2,命题显然成立.
假设当n=k(k≥1)时,命题成立,即将数列1,2,3,…,2k围成一个环,从1开始去掉,然后隔一项再去掉一个数,…,依次进行下去,最后剩余的数为2k.
则当n=k+1时,从1开始转一圈去掉一半的数,剩下2k个数,由n=k可知,最后剩下的数是剩下的第2k个数,亦即是数2k+1.
综上,命题1成立.
命题2将数列1,2,3,…,2n+k(n≥1,k<2n)的数字顺时针围成一个环,从去掉1开始,然后按顺时针方向隔一项再去掉一个数,直到最后剩下一个数,则这个数是2k.
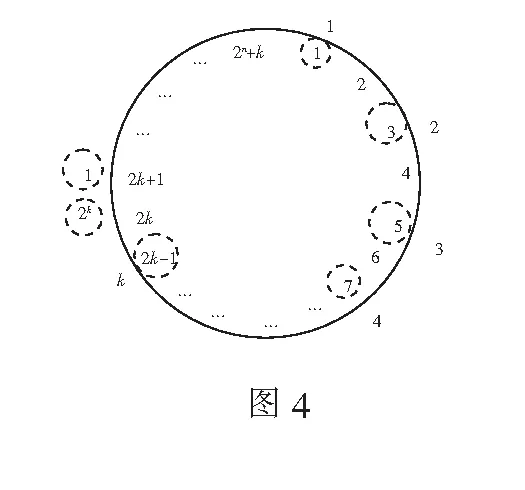
证明先从1开始,按照题目要求去掉k个数,则去掉的第k个数为2k-1,此时剩余2n个数.如图4,在这2n个剩余数中,2k+1号数相当于新数环中的1号数,2k号数相当于数环中的第2n号数.因此,由命题1知最后剩余的是第2k号.命题2得证.
四、解决问题
由2020=210+996,得n=10,k=996.所以,由命题2知文首夏令营赛题中所求最后剩余的数字为996×2=1 992.

