注重探究学习 激发学生兴趣——以“平面与平面垂直的性质”教学设计为例

罗贤旭

(浙江省丽水中学, 323000)

本文介绍“平面与平面垂直的性质”一节课的教学设计，供大家分析研究.

一、 复习回顾,引入课题

师:请同学们回顾两个平面垂直有哪些判定方法?

生:平面与平面垂直的判定定理.

师:很好!能用文字语言与符号语言表述判定定理吗?

生1:文字语言:如果一个平面经过另一个平面的一条垂线,那么这两个平面相互垂直.符号语言:a⊥β,a⊂α⟹α⊥β.

师:这位同学回答得很好,也就是说线面垂直可以得到面面垂直．说明大家对平面与平面垂直的判定定理学习得非常好!

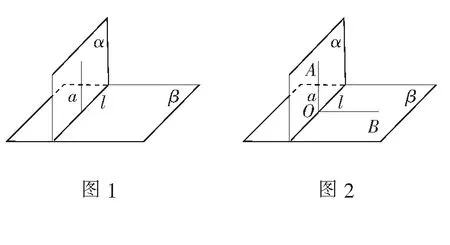
师:(PPT展示面面垂直判定定理的图形语言，如图1)除了判定定理之外,我们还有其他判定平面垂直的方法吗?

生:(思考片刻后继续沉默)

生2:二面角是直角.(回答得很轻)

师:大家觉得这位同学说得对吗?

生：(少数学生)可能.

师:(展示二面角是直角的图形，如图2)同学们,我们一起来回忆面面垂直是如何定义的.我们首先学习了二面角的概念,然后进一步学习了二面角的平面角的作法,最后定义二面角是直角的两个平面相互垂直!

生：(齐)对!(同学们都有顿时豁然开朗的感觉).

设计意图立体几何中判定定理与性质定理具有相互依存关系,通过复习回顾判定定理唤起学生对垂直概念的思考,同时也为后面性质定理的学习做了铺垫.

师:如果将判定定理中的某个条件和结论换个位置,结果还成立吗?比如说:α⊥β,a⊂α⟹a⊥β.

生:不一定成立.

师:那同学们能举出反例吗?

生:直线可能和平面平行,也可能会相交但不垂直.

师:(PPT展示学生说的两种情形，如图3)很好！这两种情况都会出现不垂直.

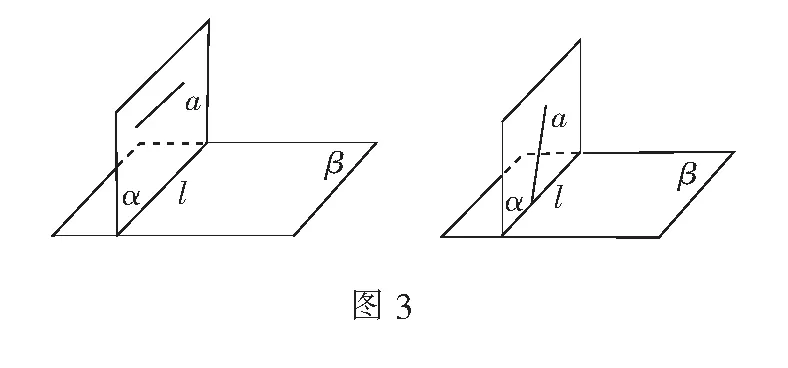
师:平面α内是否存在与平面β垂直的直线?

生：(齐)存在!

师:那这样的直线该如何作出来?同学们思考下,然后我们请一位同学上白板演示一下.

生3:在白板上老师已经画好的平面α内作一条直线a垂直于交线l.

设计意图通过改变条件与结论的方式,引导学生寻找垂直的直线,也就很自然得到本节课的要点——平面垂直的性质定理.

师:同学们作的直线一定垂直于平面β吗?

生:一定!

师:在未证明之前这还只是同学们的一种猜想,下面我们一起来证明这个猜想.

二、借助模型,论证猜想

师:在如图4所示的长方体中,面A′ADD′与面ABCD垂直,直线A′A垂直于其交线AD，直线A′A与平面ABCD垂直吗?

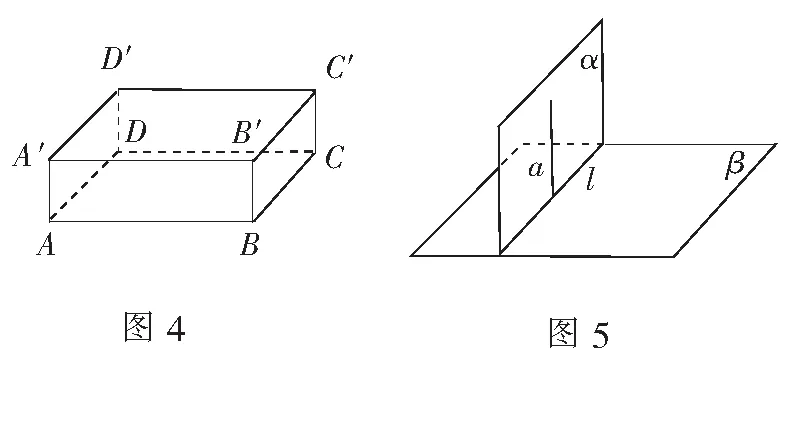
生:垂直.

师:更一般地,我们需要证明的问题是:已知α⊥β,α∩β=l,a⊂α,a⊥l,则a⊥β.(展示PPT图形如图5)同学们一起分析一下:我们现在要证明的是线面垂直,可以寻找线线垂直,那么能找到两条相交直线与已知直线垂直吗?

生4:已知条件中已有a⊥l,只要在平面β内再作一条直线与a垂直

师:嗯,请这位同学说说自己的想法.

生4:在平面β内过直线a与l的交点O作射线b⊥l,则a⊥b.

师:为什么?

生4:因为两条射线组成角的是二面角的平面角.

师:非常好,你是怎么想到这个方法的?

生4:老师开始上课时给我们复习了用直二面角判定平面垂直,所以就自然想到了.

设计意图平面垂直的性质定理的证明其实是有难度的,学生思维方法里面很难直接想到用定义,课前复习定义就为学生联想用定义法证明性质定理搭建了桥梁.

师:这就是今天要学习的面面垂直的性质定理我们一起来重新整理一下其文字语言、图形语言及符号语言.

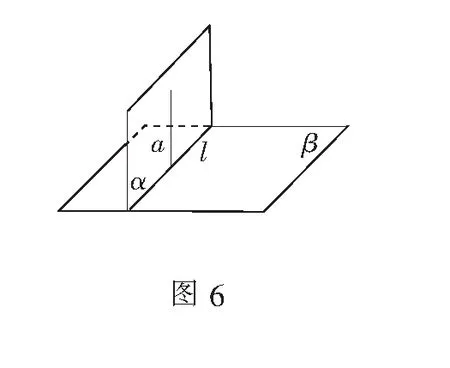
文字语言:若两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.

符号语言:α⊥β,α∩β=l,a⊂α,a⊥l⟹a⊥β.

图形语言:如图6.

三、借助模型,运用性质

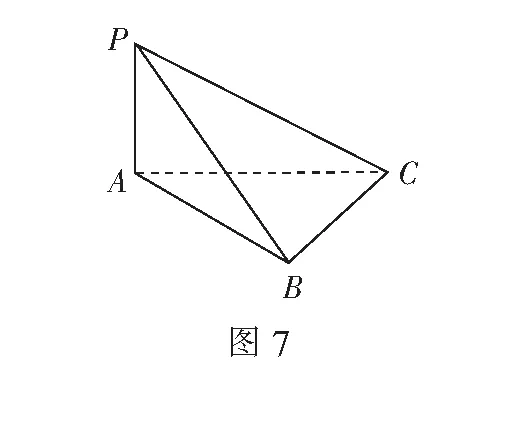
例1如图7,PA⊥平面ABC,平面PAB⊥平面PBC,求证:BC⊥平面PAB.

师:同学们思考后有想法吗?

生5:在平面PAB内只能找到一条直线PA与BC垂直,其余直线都不垂直.

师:其余直线都不垂直吗?

生:其余的直线肯定和BC垂直,因为题目是要我们证明线面垂直.

师:分析得很好!垂直的现状是肯定的,只是我们目前具有的条件很难证明他们的垂直关系,该怎么办?

生:可以过点A作AD⊥PB,那么AD就垂直平面PBC,也就垂直BC.

师:很好!你是怎么想到作这条垂线的?

生:因为题目条件是两个平面垂直,我们今天学习的面面垂直的性质定理就是由面面垂直得到线面垂直,进一步可以得到线线垂直.

师:理解非常到位．面面垂直为我们作平面的垂线提供了路径.

设计意图鳖臑是高中立体几何的重要模型,这个模型虽然很简洁,但是对于培养学生运用性质定理起到了很好的铺垫作用.

四、改变条件,生成结论

思考1在平面α⊥β的基础上,改变面面垂直的性质定理的条件,看看你能得到什么样的结论,并给出证明.

生6:过平面α外一点P作一条直线a⊥β,则直线a∥α.

师:很好!如何证明?

生6:感觉肯定平行,但我不知道如何说明.

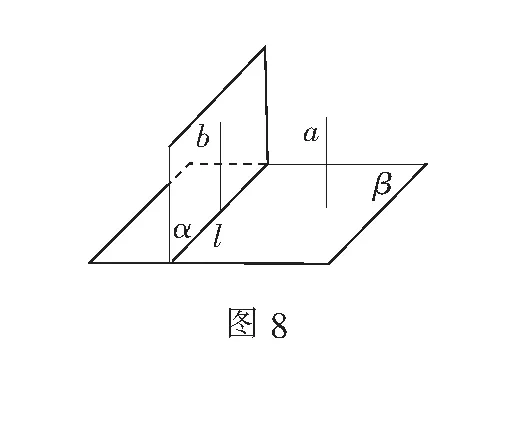
生7:可以在平面α内作一条直线b垂直于交线l(如图8),那么直线b就垂直于平面β,则由线面垂直的性质定理得到a∥b,所以a∥α.

师:这位同学给出了这个命题的证明，请问同学们还能得到其他命题吗?

生8:既然在平面外可以作一条直线,我觉得过平面α内一点P作直线a⊥β,则直线a⊂α.

师:这位同学的命题该如何证明呢?

生:(沉默)

师:同学们想想看,性质定理说平面α内垂直于交线的直线一定垂直平面β，现在反过来,我们的问题是证明过平面α内一点作平面β的垂线一定在平面α内,同学们有什么启发吗?

生9:这条直线肯定是垂直于交线的.

师:对!然后呢?

生9:过点P作交线的垂线,则这条直线就垂直于平面β,这条直线就是问题中给出的直线,所以我们只需要证明两条直线重合.

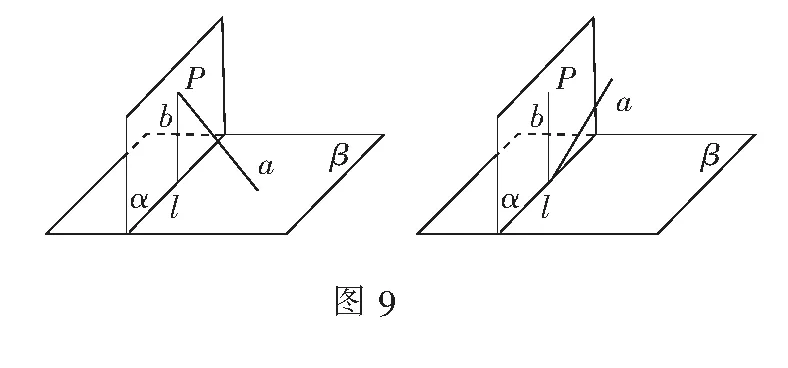
师:很好!(PPT展示图形语言如图9)其实,过平面外一点只能作一条直线与已知平面垂直,我们通过探究发现这两条直线是同一条直线 这种证明方法在数学中称为同一法!

五、增加条件,生成结论

思考2在α⊥β的基础上,增加一个垂直于平面β的平面γ,你又能得到什么样的结论?

生10:如果增加条件γ∥α,且γ∩α=m,则m∥l.

师:这位同学得到的这个结论应该是我们平面与平面平行的性质的特殊情况.

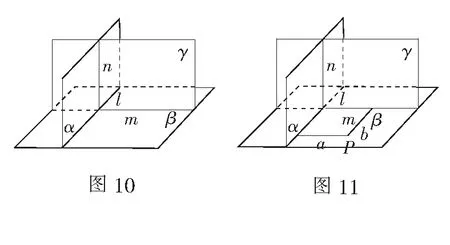
生11:我觉得增加的平面如果与α不平行,那么就会相交．即增加条件γ∩α=n,γ∩β=m,则n⊥β.

师:很好!这位同学给出了不同的条件和结论,下面分组讨论如何证明?

小组1: 我们用线面垂直的判定定理证明先在平面β内取一点P,过点P在平面β内作a⊥l,b⊥m,再由面面垂直的性质定理得a⊥α,则a⊥n;同理可得b⊥n,因为a∩b=P,则n⊥β.

师:小组1几位同学讨论的结果非常好,我想问你们怎么想到这样证明的?

小组1: 要证线面垂直,需找线线垂直，首先想到今天学习的线面垂直性质定理,证明的难点是找到两条相交直线,然后我们联想到鳖臑那个例子中构造辅助线的方法.

师:能够联想到例题的方法,很好！ 其他组还有用不同的方法证明的吗?

小组2:我们通过线面平行的性质定理证明了结论，先在平面α内作a⊥l,则a⊥β;在平面γ内作b⊥m,则b⊥β,进而a∥b. 因为b⊂γ,则a∥γ.又α∩γ=n,由线面平行的性质定理得a∥n,所以n⊥β.(同学们响起掌声)

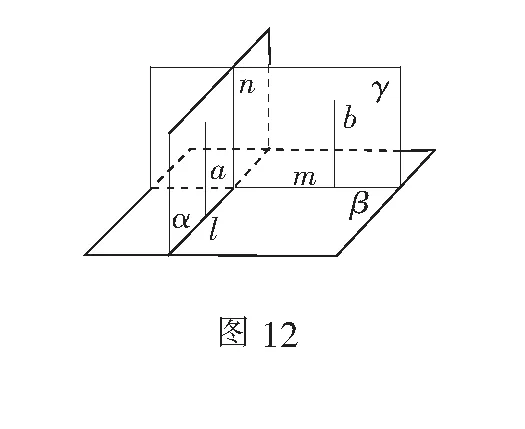
师:同学们非常善于思考,这组同学们能够将前面所学线面平行的性质定理应用到今天的证明过程中,实现了知识间的相互转化.

六、归纳总结拓展深化

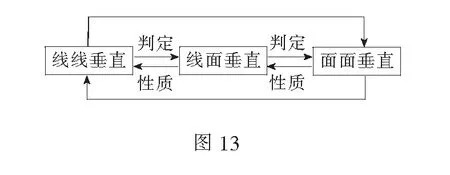
师:下面请同学们归纳一下线线垂直,线面垂直,面面垂直的相互转化关系(白板书写).

生:上黑板完成三者的相互转化关系,将垂直关系用箭头串联起来(图13).