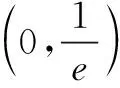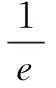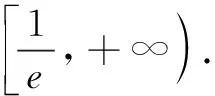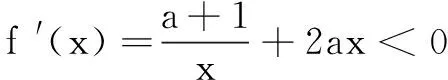寻找相似的你
——谈“同构式”在解题中的应用
张晓飞
(江苏省南京师范大学第二附属中学,211900)
2020年高考已经落下帷幕,纵观各地的高考试卷,发现在全国理科一卷和全国文科二卷中出现了如下的两道题,它们涉及一个知识点——同构式.
试题1若2a+log2a=4b+2log4b,则( )
(A)a>2b(B)a<2b
(C)a>b2(D)a 试题2若2x-2y<3-x-3-y,则( ) (A)ln(y-x+1)>0 (B)ln(y-x+1)<0 (C)ln|y-x|>0 (D)ln|y-x|<0 这里说的同构式,指的是结构、形式相同的解析式.对于一个方程或不等式,经过适当变形、整理后,使其左、右两边表示成“结构相同”的式子,由此构造相应的函数,利用函数的单调性可使问题简便解决. 例如,在试题1中,将2a+log2a=4b+2log4b变形为2a+log2a=22b+log22b-1.构造函数f(x)=2x+log2x,利用f(x)在区间(0,+∞)单调增,可得a<2b,选B.在试题2中,2x-2y<3-x-3-y变形为2x-3-x<2y-3-y.构造函数g(x)=2x-3-x,由g(x)在R上单调增,可得x 同构式在函数中的应用主要体现在方程和不等式的相关问题中,笔者以下从几个方面具体说明. 评注由方程组中方程的同构性转换思维方向,将函数的定义域与值域问题转化为新方程解的存在性问题,揭示了问题的本质,简化了问题求解途径. 例2已知cos5θ-sin5θ<7(sin3θ-cos3θ),θ∈[0,2π),求θ的取值范围. 评注观察不等式的函数与结构特征再变形,是生成同构式的关键、构造函数的前提条件,由此利用函数单调性可顺利解题. 例3已知函数f(x)=aex-lnx-1. (1)设x=2是f(x)的极值点,求a及f(x)的单调区间; 解(1)略. 解当a≥1时,对任意x∈(0,1),g(x)>0>f(x),g(x)>f(x)显然恒成立. 例5已知函数f(x)=(a+1)lnx+ax2+1 (a<-1),对任意x1,x2∈(0,+∞),恒有不等式|f(x1)-f(x2)|≥4|x1-x2|成立,求实数a的取值范围. 评注本题是二元不等式恒成立问题,求解的常规思路是首先根据f(x)的单调性对不等式进行去绝对值的操作,再由同构思想变形为f(x1)+4x1≥f(x2)+4x2,将二元函数问题通过构造函数H(x)=f(x)+4x减元,转化为一元函数最值问题进行求解. 纵观上述例题,不难发现此类题目实际上是命题者将原先形式明显、结构统一或者相似的问题经过加工、调整变成看似没有规律的复杂的问题.而解题者要做的工作就是还原题目的本质,使其天然去雕饰,清水出芙蓉.一、方程问题
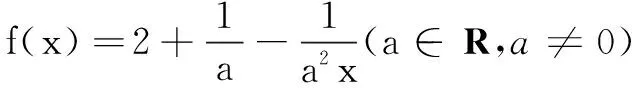

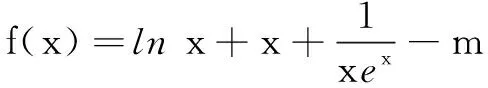
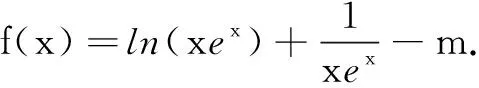
二、解不等式问题
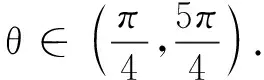
三、不等式恒成立问题