主题引领，提升思维

傅广辉 朱敏

摘要：主题拓展课要以一定的主题为线索统领全课，通过适当的联系和变化，引导学生不断开阔视野、丰富认识、把握本质，逐步完善知识体系，提升数学思维，积淀数学素养。《多变的圆柱体》主题拓展课，以苏教版小学数学教材中的“A4纸卷圆柱”问题为基础进行变式，引导学生探究圆柱体积和表面积的其他计算方法，帮助学生开阔数学视野，打破思维定式，形成对数学知识结构化的思考，感悟转化的数学思想方法。

关键词：主题拓展课结构化思考转化思想《多变的圆柱体》

作为小学数学总复习课的一种课型，主题拓展课要以一定的主题（可以是小学数学中的核心概念、重要结论、基本思想、重要方法、关键模型等，也可以是数学文化、数学精神）为线索统领全课，通过适当的联系和变化，引导学生不断开阔视野、丰富认识、把握本质，逐步完善知识体系，提升数学思维，积淀数学素养。

《多变的圆柱体》主题拓展课以苏教版小学数学六年级下册《圆柱和圆锥》单元《整理与练习》板块《探索与实践》栏目的第14题“A4纸卷圆柱”问题为基础进行变式，引导学生探究圆柱体积和表面积的其他计算方法，以期达成如下教学目标：（1）经历探究圆柱体积和表面积其他计算方法的过程，了解其原理，学会从不同的角度分析、解决问题，开阔数学视野，打破思维定式;（2）体会新旧知识（不同计算方法）之间的联系，形成对数学知识结构化的思考;（3）通过操作、观察、对比、分析、推理等活动，加深对圆柱体积和表面积计算公式推导过程的理解，感悟转化的数学思想方法。本节课的教学过程如下：

一、教材引入，温故知新——1张A4纸卷圆柱

（一）激趣

师今天的研究从一张A4纸开始。你能把一张A4纸卷成圆柱吗？动手试一试吧！

（学生操作。）

生（展示，如图1）以A4纸的短边为高，卷成一个圆柱。

生（展示，如图2）以A4纸的长边为高，卷成一个圆柱。

师同样一张A4纸卷成的两个圆柱，体积相等吗？哪个圆柱的体积大？

生①号圆柱体积大，之前书上有过类似的练习题。

师（呈现教材中的练习题，见图3）回顾一下，之前是怎样比较这两个圆柱的体积的？

生先测量数据，再用“体积=底面积×高”的公式计算，然后比较。

师谁能说一说这个体积公式是怎么得来的？

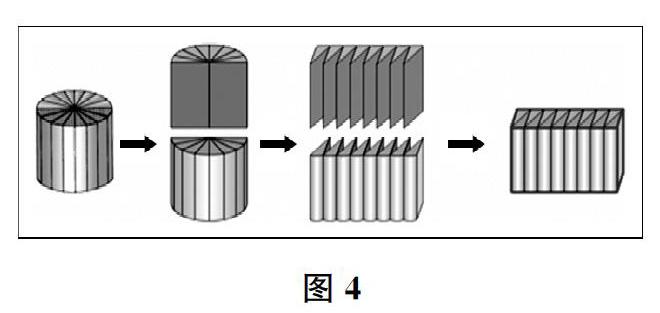
生把圆柱沿高切开，拼成近似的长方体，我们发现，圆柱的底面积就是长方体的底面积，圆柱的高就是长方体的高……

（课件演示如图4所示的变化过程。）

（三）引新

师老师不计算，只看一眼，就知道谁的体积大。你信吗？

（学生表示不信。）

师（课件演示如图5所示的变化过程）如果把拼成的长方体像这样翻转，那么长方体的底面积和高与圆柱又有怎样的关系呢？请大家仔细观察。

生我发现，翻转后长方体的底面积正好是圆柱侧面积的一半，长方体的高就是圆柱的底面半径。

生我们可以再编一个体积计算公式，就用侧面积的一半乘底面半径。

师真善于观察和总结！有了这个体积计算方法，现在你们再仔细地看一看、想一想：为什么老师一眼就能看出①号圆柱的体积大？

（学生独立思考，同桌讨论。）

生我知道了！同样的A4纸分别卷成了两个圆柱的侧面，因此，它们的侧面积相等，半个侧面积自然也相等。而①号圆柱的底面半径比②号圆柱大，所以，根据圆柱的体积=侧面积的一半×底面半径，就能知道①号圆柱的体积更大。

生原来，在侧面积相等的情况下，谁的底面半径大，谁的体积就大。

生这个公式太有意思了！有了它，就能更快地解决之前的卷圆柱问题了……

师很棒！你们发现了老师的秘密武器。

[评析：“1张A4纸卷圆柱”是教材中的练习题。学生习惯用圆柱体积的“底面积×高”公式计算，得出结论。这里，教师引导学生在已有经验的基础上，拓展数学视野，打破思维定式，探究圆柱体积的其他计算公式，從而快速地解决问题。这样的拓展探究以教材为依托，以学情为起点，以解决具体的问题为目标，以操作、观察、质疑、讨论等活动为手段，真实、自然、结构化、有价值。]

二、操作深入，学会思维——2张A4纸卷圆柱

（一）延展

师如果将2张A4纸拼接在一起（接头处忽略不计），再卷成圆柱，可以卷成多少种不同的圆柱呢？

（学生同桌合作操作。）

生（出示图6）一共有4种不同的卷法，A4纸的长边拼接在一起可以卷成2种，宽边拼接在一起也可以卷成2种。

（二）分析

师你知道它们中谁的体积最大吗？还需要算一算吗？

（学生自主思考，小组交流。）

生不需要计算，还是可以用刚才的公式推理出来。

生①号圆柱的体积最大。你们看，这4个圆柱的侧面都是用2张A4纸拼成的，所以侧面积是一样的。根据刚才的新公式，我们还是只要比哪个圆柱的底面半径大，就可以了。

生你们看，①号圆柱是把两条长边拼接在一起作为底面周长的，当然半径最大，体积也就最大。

师你们的互相补充让大家对这个问题有了更深入的理解，真棒！

（三）丰盈

师小小的一次翻转让我们收获了别样的学习体验，还想继续换个角度看问题吗？（课件演示如图7所示的变化过程）如果把拼成的长方体像这样翻转，是不是还能得出别的体积计算方法呢？请你仔细观察。

生真的有发现！我看到，长方体的底面积是切面的一半。

师观察得真仔细！这个切面在数学上叫作圆柱的“轴截面”。

生我发现翻转后长方体的底面积刚好是轴截面面积的一半，高是圆柱底面周长的一半。

生还可以编出一个“新”的公式：圆柱的体积=轴截面面积的一半×底面周长的一半。

生其实，这三个体积公式在本质上是一样的，得看你在什么情况下用……

师你们的发现太有趣了，你们的总结更是让我刮目相看！数学就是这么神奇，换个角度看一看、想一想，可能就会有意想不到的收获。

[评析：由“1张A4纸卷圆柱”拓展到“2张A4纸拼接后卷圆柱”，问题更复杂，卷法更多样，但是，运用之前探究得到的公式，可以快速解决。由此，学生充分认识到不同问题的相同本质，以及“新”公式的大作用。接着，继续对圆柱体积的计算公式进行拓展，在学生的“最近发展区”内着力，为他们提供有挑战性的思维内容，引领他们进一步形成对数学知识结构化的思考。]

三、拓展视野，提炼思想——圆柱表面积公式的“再创造”

（一）拓展

师刚才，我们一起经历了圆柱体积公式的“再创造”。受此启发，圆柱的表面积公式能否有不同的表达呢？（稍停）咱们先来理一理之前学习的圆柱表面展开情况，谁来介绍？

生把圆柱的侧面沿高展开，可以得到一个长方形，圆柱的底面是两个完全相同的圆形，圆柱的表面积是这一个长方形和两个圆形面积的和。

师熟悉的地方也会有新的风景，想不想知道？（稍停）提示一下：根据之前圆面积的学习经验，底面这两个圆可以转化成什么图形？

生两个长方形。

师那么，这三个长方形能不能拼接在一起？它们之间又会创造出怎样的精彩呢？期待你的发现。

（学生组内研讨后，教师引导总结，课件演示如图8所示的变化过程。）

生太不可思议了，它居然拼成了一个大长方形！

生这个长方形的长是圆柱的底面周长，宽是圆柱的高与底面半径的和。

生我知道啦，圆柱的表面积还可以表达成“底面周长×（高+底面半径）”。

（二）提炼

师同学们，我们在对圆柱体积和表面积“再研究”的过程中，都用到了一种很重要的数学思想方法，你们知道是什么吗？

生换个角度看问题，数学真奇妙！

生不要总想着套公式，我们也可以自己“创造”公式。

生我觉得是“转化”，它让我们看到了图形之间的联系，看到了更多的可能。

师没错。转化是一种十分重要的数学思想方法。

[评析：由“圆柱体积公式的‘再创造”拓展到“圆柱表面积公式的‘再创造”，进一步渗透逻辑推理（包括类比、归纳、演绎等）的思维方式，助力学生形成对数学知识结构化的思考。对转化思想的提炼揭示是本节课的点睛之笔，其目的是充分达成“提升思维”的教学目标。]

参考文献：

[1] 蒋守成，朱敏.对数学主题拓展教学的内涵与价值的思考[J].江苏教育，2012（16）.

[2] 陈东栋，黄玲玲.基于小学数学教材的主題拓展数学[J].江苏教育，2012（16）.