例析含动滑轮的牵连体速度问题

◇ 湖北 许 文

在运动的合成与分解中，常见与动滑轮有关的牵连体速度问题．对这类问题，学生往往因不能正确判断物体合运动与分运动的关系而求解出错，求解这种牵连体的速度问题，可以用微元法、求导法、转换参考系法、能量守恒法等方法进行分析与求解．

例1如图1所示，物体A置于水平面上，A的前端固定一动滑轮B，右侧高台上有一小定滑轮D，一根轻绳一端固定在C点，再绕过两滑轮B、D．其中绳BC段水平，当以速度v0拉绳子自由端时，物体A沿水平面运动，当跨过动滑轮B的两段绳子夹角为α时，物体A运动的速度大小v是多少?

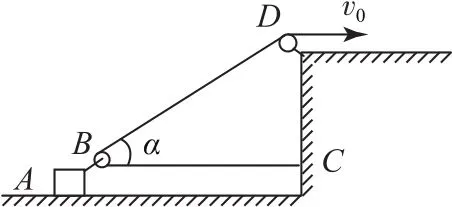
图1

解析

物体A与动滑轮相连，物体A运动的速度即为动滑轮运动的速度．动滑轮运动的速度与动滑轮两边绳子移动的速度有关联．

方法1（微元法） 如图2所示，设在很短的时间Δt内，物体向右运动Δx，绳拉出长度 Δl＝Δx＋Δxcosα，故有·（1＋cosα），即v0＝v（1＋cosα），可得

图2

方法2（导数法） 如图3所示，有，则x＋l＝x＋，两边对时间t求导，有

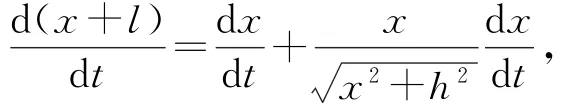
图3

即v0＝v（1＋cosα），可得

图4

方法3（转换参考系法） 小动滑轮B与物块A的速度相同．如图4，以小动滑轮B为参考系，其上段绳上的某点P与下段绳上的某点Q相对小动滑轮的速度大小相等，即

方法4（能量守恒法） 设轻绳上的拉力大小为F，由系统的能量守恒知，拉绳自由端拉力的功率与两段绳拉动滑轮的功率和相等，即Fv0＝Fv＋Fvcosα，可得

点评

以上方法1基于平均速度与瞬时速度的关系，用到了微元法，需要用到数学上的近似计算，这是一种处理变化问题的基本解法；方法2基于速度的物理意义，用到了求导法，通过几何知识找出牵连体运动的位移大小关系，这种解法对数学知识要求较高，但这是一种实用的解法；方法3利用了转换参考系法，同一绳子绕过动滑轮，动滑轮两边绳子上的点相对动滑轮移动的速度大小相等，这是一种最具内涵的解法；方法4利用了能量守恒，巧妙地利用牵连体间内力的机械功率关系求解，求解过程简洁，给人一种高屋建瓴之感，是一种最为巧妙的解法．

例2如图5所示，AA1、BB1是固定于天花板上的两光滑竖直杆．细绳的一端固定在B点，另一端拴在套于杆AA1的珠子D上，另一颗珠子C穿过细绳且套在杆BB1上．已知珠子C以速度v1匀速下落，当细绳与杆AA1夹角成θ时，珠子D上升的速度v2大小为（ ）．

图5

解析

本题中的珠子C相当于小动滑轮．

方法1（微元法） 设在很短时间Δt内，珠子C下落距离v1Δt运动到C1处，珠子D上升距离v2Δt运动到D1处（如图6所示）．在AA1上取点E，使CE平行且等于C1D1．在CD上取点F使CF＝CE，有DF＝CC1，即

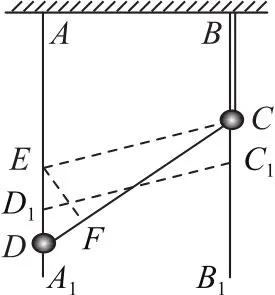
图6

方法2（转换参考系法） 以珠子C为参考系，珠子D以相对速度v2＋v1上升，它是相对C的转动速度u与平动速度v1的合速度（如图7所示）．有v1＝（v2＋v1）cosθ，可得

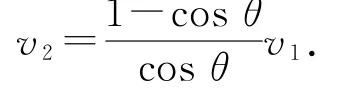
图7

方法3（能量守恒法）如图8，设细绳上的张力为F，由于C、D两珠子系统的机械能守恒，则两珠子受绳子拉力的功率和为零，即

方法4（相对法） 如图9所示，绳子D端在CD间移动的速度大小为v2cosθ，而CD间的C端绳子被拉出去的速度大小为v1－v1cosθ，有v2cosθ＝v1－v1cosθ，可得

方法5（导数法） 设两竖直杆间的距离为l，绳总长为L．如图10所示，则开始时珠子C与天花板的距离为，珠子D与天花板的距离为h2＝，则有

（注:上式求导第一个“－”表示h2在减小）

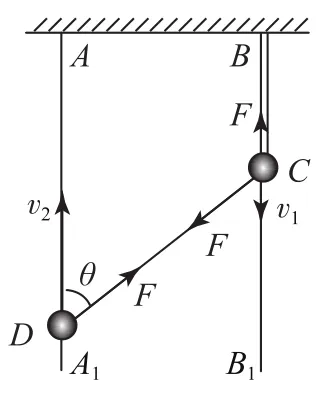
图8

图9

图10

总之，对于涉及动滑轮的牵连体速度问题，由于与动滑轮连接物体的速度分解较复杂，可以采用转换参考系的方法，利用相对速度间的关系进行分析求解．另外，微元法与求导法都是分析此类问题的基本方法，能量守恒法是分析求解这类问题的最巧妙方法．