斜坡地质灾害敏感性评价中地势起伏度提取最佳尺度研究

张明媚，薛永安

(1.太原理工大学 矿业工程学院，太原 030024；2.山西能源学院 地质测绘工程系，山西 晋中 030600)

斜坡地质灾害敏感性是指在特殊地形或某些因素作用下发生滑坡、崩塌灾害的可能性[1]，地质灾害敏感性评价的本质就是利用数学语言来表达在给定的地质环境条件下地质灾害在空间上的发生概率[2-3]。目前，对于地质灾害敏感性评价研究已有许多成果。ACHOUR et al[4]基于层次分析法和信息量模型开展了滑坡敏感性研究。YALCIN et al[5]的对比研究表明层次分析法对滑坡敏感性的分区与实际情况更加符合。NICU et al[6]采用坡度、高程、曲率、岩性、降水、土地利用、地形润湿性指数、地形、坡向、平面曲率和距离河流距离等11个条件因子对滑坡的敏感性程度进行了统计分析。HONG et al[7]选取坡度、坡向、海拔、平面曲率、剖面曲率、岩性、距离断层距离、距离河流距离、距离道路距离、土地利用、归一化植被指数等15个因子作为滑坡灾害敏感性评价因子集合。THAI et al[8]选用坡度、曲率、海拔等15个影响因子作为滑坡灾害敏感性评价因子集合。而KALANTAR et al[9]对Dodangeh流域进行滑坡灾害敏感性评价研究中采用的因子为曲率、平面曲率、剖面曲率、高程、坡度、坡向、距离断层距离、距离河流距离、地形湿度指数、河流水力指数、地形粗糙度指数、沉积物搬运指数、岩性及土地利用。在上述这些研究中，以高程、坡度、坡向、曲率等为代表的数字地形因子是斜坡地质灾害敏感性评价的重要因子。

然而，作为描述一个区域地形特征的宏观性指标，地势起伏度指在一个特定的区域内，最高点海拔高度与最低点海拔高度的差值，它能反映地表起伏变化，与斜坡地质灾害的发生存在很大的相关性[10]。按照地貌发育的基本理论，一种地貌类型存在一个使最大高差达到相对稳定的最佳分析区域，传统方法是利用栅格窗口的递增方法来寻找最佳的分析窗口[11]。这是地貌分析中地势起伏度计算的最佳统计单元思路，即随着统计单元半径的增大，地势起伏度随之变化，到达某一临界点后趋于稳定，临界点即为地势起伏度的最佳统计单元，也是真实反映地形起伏的DEM地势起伏度提取单位面积。针对地势起伏度最佳提取单元的研究[12-13]，众多学者以不同尺度的DEM在不同实验区开展了研究工作，结果各异。涂汉明等[14]通过对全国600个样点和2个小区的详细研究，运用模糊数学方法，确定了全国地势起伏度最佳统计单元为21 km2.张军等[15]则得出基于1∶250 000 DEM的新疆地势起伏度计算的最佳统计单元为2.56 km2.赵斌滨等[16]基于90 m分辨率SRTM-DEM数据提取得到中国地势起伏度的最佳统计单元面积为2.25 km2.王让虎等[17]基于ASTER GDEM数据提取得到中国东北地区地形起伏度的最佳统计单元面积为2.62 km2.陈学兄等[18]以30 m分辨率ASTER GDEM数据为基础，运用均值变点分析法计算得到0.260 1 km2为山西地形起伏度提取的最佳统计单元。杨艳林等[19]基于ASTER GDEM数据分析得出长江中游的地形起伏度最佳分析窗口为19×19像元，面积约0.324 9 km2.而郭芳芳等[20]从地势起伏度分析在区域斜坡灾害评价中的应用出发，寻找反映斜坡点对应的真实地势起伏度单元，对不同统计单元地形起伏度值与斜坡个数统计曲线峰值分布特征进行分析，确定了研究区地形起伏度最佳统计单元面积为4 km2.

基于上述研究，本文以山西省太原市西山地质块体为研究区，以ASTER GDEM V2为地势起伏度提取数据源，以2012年斜坡地质灾害分布信息为斜坡灾害发育敏感性评价数据源，以均值变点法开展斜坡灾害敏感性评价中地势起伏度因子最佳提取单元研究。

1 数据与方法

1.1 研究区与数据源

研究区位于山西省中部、太原盆地的北端，北接太原市阳曲县，西邻太原市古交市、清徐县，东邻太原盆地，南靠太原市清徐县，包括太原市尖草坪区、万柏林区和晋源区，总面积441.063 km2，见图1.研究区的地理坐标为东经112°15′03″-112°29′25″，北纬37°38′54″-38°01′14″.

图1 研究区地理位置图Fig.1 Geographical map of the studied area

1.1.1DEM数据

ASTER GDEM(先进星载热辐射和反射仪全球数字高程模型)是根据NASA的新一代对地观测卫星Terra的详尽观测结果制作完成的，其全球空间分辨率约为30 m，垂直分辨率为20 m，空间参考为WGS84/EGM96[21].ASTER GDEM目前共有两版数据，本文研究采用第2版，于2011年10月发布，数据来源于中国科学院计算机网络信息中心地理空间数据云平台。以研究区ASTER GDEM V2重采样后30 m分辨率DEM为基准数据(数据参数及精度见表1).

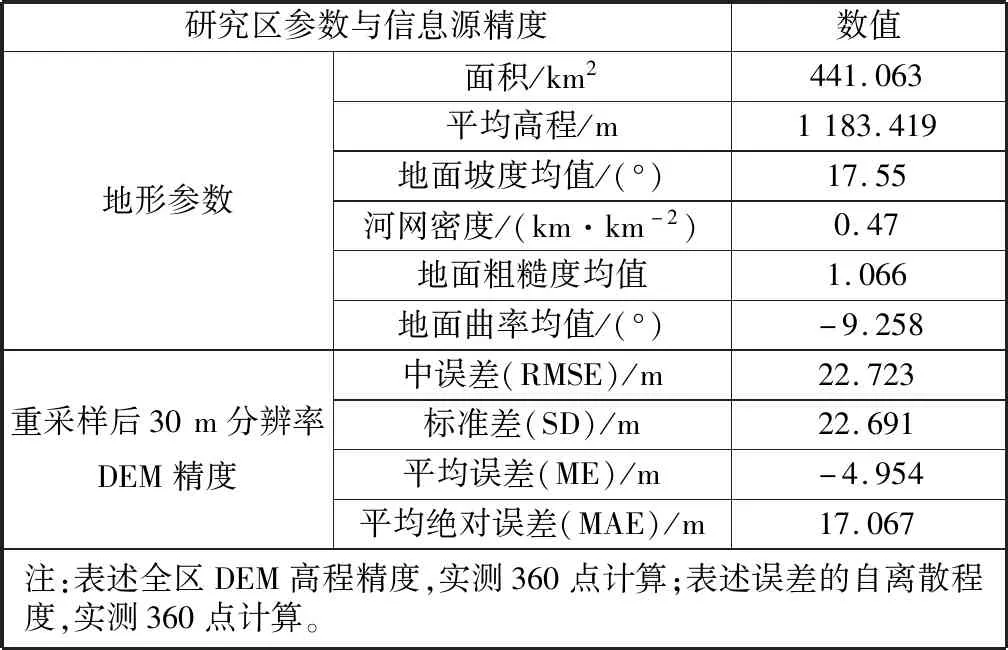
表1 研究区主要地形参数及信息源精度Table 1 Main terrain parameters and information source accuracy of the studied area

1.1.2斜坡地质灾害数据

从太原市规划和自然资源局收集到研究区2012年斜坡地质灾害分布信息，见图2.

图2 研究区斜坡地质灾害空间分布图Fig.2 Spatial distribution of slope geological hazards in the studied area

1.2 均值变点法

目前，最佳地势起伏度统计单元的寻找主要依赖人工判断，以平均地势起伏度随统计单元面积变化的转折点作为最佳统计单元面积，也就是人工判断曲线上由陡变缓的位置；这种判断方法显然主观性太强，不够准确。随着最佳地势起伏度统计单元研究工作的深入[22]，统计学领域的均值变点法逐渐被用作计算曲线上由陡变缓点位的客观方法。

均值变点法的原理及步骤如下[23]：

1) 检验是否存在变点，即检验原假设H0是否存在变点。若H0被接受，则该数据序列没有变点；若H0被否定，则假设该序列中至多存在q个变点，对m1，m2，…，mq变点进行估计。

2) 估计变点个数。

3) 估计变点处均值的跳跃度。

在实际估计中，如果先验知识足以肯定序列中变点的存在，则可跳过步骤1)而直接进入后几步。

均值变点问题的离散数据模型如下。

设xt=at+et,t=1,2,…,N，则

a1=…=am1-1=b1，am1=…=am2-1=b2，…，amq=…=aN=bq+1.

(1)

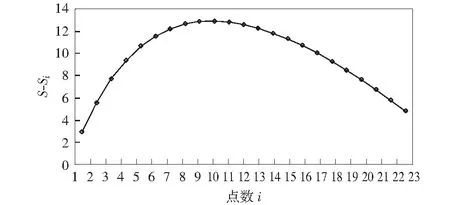
式中：1

H0∶b1=b2=…=bq+1.

(2)

此处特别强调本检验与多样本检验的差别，即此检验中m1,m2,…,mq为未知。

原假设H0的检验步骤如下。

1) 令i=2,…,N，每个i将样本分为两段：

x1,x2,…,xi-1和xi,xi+1,…,xN.

(3)

(4)

2) 计算统计量：

(5)

3) 计算期望值：

E(S-Si),i=2,3,…,N.

(6)

4) 求极大值：

(7)

在平均意义下认为：

S*=min(S2,…,SN) .

(8)

5) 取检验显著性水平为α，计算C值：

C=σ2(2lg lgN+lg lg lgN-lg π-2lg(-0.5lg(1-α))) .

(9)

如果σ2未知，则用下面估计来替代：

(10)

6) 如果S-S*>C，则否定H0，认为无变点，否则接受H0，该检验有渐近水平α.

平均来说，如果序列中存在变点，则S和Si的差距会因变点的存在而增大，所以均值变点法原理明确，操作简单。同时，均值变点法对只有一个变点的检验最为有效，存在多个变点时有可能因为均值的多次升降而抵消了S和Si之间的差距。

2 结果与讨论

2.1 平均地势起伏度与统计单元之间的关系

基于ArcGIS平台，利用邻域分析法提取研究区不同面积单元的地势起伏度，提取单元分别为30 m分辨率DEM数据网格的2×2，3×3，4×4，5×5，…，25×25，对应的提取单元面积(km2)分别为：0.003 6,0.008 1,0.014 4,0.022 5,0.032 4,0.044 1,0.057 6,0.072 9,0.090 0,0.108 9,0.129 6,0.152 1,0.176 4,0.202 5,0.230 4,0.260 1,0.291 6,0.324 9,0.360 0,0.396 9,0.435 6,0.476 1,0.518 4,0.562 5，共24个面积单元。经统计，研究区不同提取单元大小与平均地势起伏度之间关系如表2所示。

由表2可以看出，随着提取的地势起伏度统计单元的增大，研究区平均地势起伏度呈现上升趋势，从最小的13.53 m上升到173.96 m，这有助于分析研究区斜坡地质灾害发育与地形起伏之间的关系。至于哪个尺度的分析窗口是最佳窗口，可以通过区域地势起伏度与斜坡地质灾害发育之间的关系进行客观的分析评价。

表2 研究区不同统计单元与平均地势起伏度之间的关系Table 2 Relationship between statistical unit and average relief amplitude of the area

以统计分析单元面积为横坐标，相应的平均地势起伏度计算值为纵坐标，对地势起伏度随统计单元面积的变化情况进行拟合，结果如图3所示。

对于不同统计单元面积与所提取地势起伏度之间的关系，通过对数方程进行拟合，得到拟合曲线方程。通过统计学检验，拟合效果良好，拟合方程为：

y=34.097lnx-52.50,R2=0.972 9 .

(11)

式中：y为平均地势起伏度，m；x为统计单元面积，km2；R2为决定系数。

从图3的曲线变化趋势来看，应有1个变点存在，过了变点后地势起伏度的增速变缓，而这个变点所对应的面积就是研究区提取地势起伏度的最佳统计单元面积。

图3 地势起伏度与统计单元面积对应关系拟合曲线Fig.3 Fitting curve of the corresponding relation between relief amplitude and area of statistical unit

2.2 地势起伏度提取最佳统计单元分析

对不同统计单元的平均地势起伏度、不同统计单元地势起伏度分级中的斜坡地质灾害峰值、地势起伏度峰值进行统计，结果见图4.

图4 平均地势起伏度、地势起伏度峰值、斜坡地质灾害峰值与统计单元关系图Fig.4 Relationship between average value of relief amplitude, peak value of relief amplitude, and peak value of slope geological hazards as one side and statistical unit as another side

根据图4统计结果分别构建样本序列，利用均值变点法的公式编制Excel程序，计算样本序列的统计量S和Si，求得S-Si(见表3)，构建S与Si差值的变化拟合曲线。

表3 均值变点法分析统计结果Table 3 Statistical results of mean change point

平均地势起伏度样本序列S值为16.994 5，S与Si差值的变化曲线见图5.地势起伏度峰值样本序列S的值为20.130 4，S与Si差值的变化曲线见图6.斜坡地质灾害峰值样本序列S的值为89.359 3，S与Si差值的变化曲线见图7.

图5 基于平均地势起伏度的S-Si变化曲线Fig.5 Variation curve based on average value of relief amplitude S-Si

图6 基于地势起伏度峰值的S-Si变化曲线Fig.6 Variation curve based on peak value of relief amplitude S-Si

图7 基于斜坡地质灾害峰值的S-Si变化曲线Fig.7 Variation curve based on peak value of slope geological hazards S-Si

2.3 讨论

1) 图4显示，每一种统计单元都存在一个斜坡地质灾害发育的峰值区间，随统计单元的增大，峰值逐渐减小，到达某一个临界值后峰值衰减趋于稳定。

2) 图5显示，i为11时，S与Si差值达最大，i=11处即为变点，对应统计单元为12×12网格。因此，由平均地势起伏度以均值变点法来分析得到研究区的最佳地势起伏度提取单元为12×12网格，最佳统计面积为0.129 6 km2.

3) 图6显示，i为11时，S与Si差值达最大，i=11处即为变点，对应统计单元为12×12网格。因此，由地势起伏度峰值以均值变点法来分析得到研究区的最佳地势起伏度提取单元为12×12网格，最佳统计面积为0.129 6 km2.

4) 图7显示，i为8时，S与Si差值达最大，i=8处即为变点，对应统计单元为9×9网格。因此，通过斜坡地质灾害峰值以均值变点法来分析得到研究区的最佳地势起伏度提取单元为9×9网格，最佳统计面积为0.072 9 km2.

5) 对比三种样本序列所计算得到的最佳地势起伏度提取单元，使用平均地势起伏度和地势起伏度峰值样本序列计算结果一致，均为12×12网格，而斜坡地质灾害峰值样本序列计算结果则为9×9网格。作为客观存在的区域地貌特征因子，斜坡地质灾害演变频繁，而平均地势起伏度演变较小。因此，以研究区数字地貌角度分析，基于平均地势起伏度所计算的最佳提取单元更合理；而以地质灾害发育角度分析，基于斜坡地质灾害峰值所计算的最佳提取单元则更合理。

6) 针对斜坡地质灾害敏感性评价中地势起伏度最佳统计单元开展研究，重点关注的是研究区地势起伏度与斜坡地质灾害发育之间的关系，因此所寻找的是能反映地势起伏度与斜坡地质灾害发育之间关系的最佳统计单元，而不是数字地貌研究中区域地势起伏度计算的最佳统计单元。因此，选择9×9网格作为研究区斜坡地质灾害敏感性评价中地势起伏度因子最佳提取单元。

3 结论

1) 地势起伏度与统计单元面积之间存在显著的对数变化关系，研究区内地势起伏度随统计单元面积的增大而迅速增大，当统计单元面积达到一定数值后，增大速度逐渐变缓，最后近似趋于平稳，这为开展地势起伏度最佳提取单元提供了基础。

2) 地势起伏度提取最佳统计单元与地质灾害分布峰值、平均地势起伏度和地势起伏度峰值之间存在明显的相关性，目前的研究主要基于平均地势起伏度，利用均值变点法或主观方式分析确定最佳提取单元，这给斜坡地质灾害敏感性评价带来一定的不确定性，所以应综合三种情况开展统计并综合分析后确定研究区地势起伏度最佳统计尺度。

3) 以研究区ASTER GDEM重采样30 m分辨率DEM和2012年斜坡类地质灾害空间分布信息为数据源，以2×2，3×3，…，25×25共24个分析窗口提取了研究区的地势起伏度，以均值变点法对不同统计单元的平均地势起伏度、不同统计单元地势起伏度分级中的斜坡地质灾害峰值、地势起伏度峰值进行统计分析。综合三种样本序列计算结果，本文选择9×9网格作为研究区斜坡类地质灾害敏感性评价时的最佳地势起伏度提取单元，这为研究区斜坡类地质灾害敏感性评价研究提供了可靠的地势起伏度因子，同时也为同类研究提供了数字地形因子较为准确的提取方法。