基于深度学习的fMRI个体流体智力预测方法
温 昕,董 立,杨 洁,李鹤纯,相 洁,郭 浩,陈俊杰
(1.太原理工大学 信息与计算机学院,太原 030024;2.电子科技大学 生命科学与技术学院,成都 611731)
功能磁共振成像(functional Magnetic Resonance Imaging,fMRI)技术的广泛应用使我们能够建立大脑功能连接模式与疾病、行为之间的关系[1-2]。其中,基于fMRI的功能连接(functional connectivity)分析广泛用于揭示不同人群之间的脑功能差异(如疾病和老化)[3-5]。在这些研究中,功能连接的个体差异通常被认为是噪声,很少用于探索大脑的功能变化。然而,最新研究表明,功能连接的个体差异包含了丰富的脑活动信息,反映大脑功能连接模式的变化[6-7]。这表明,描述、理解和预测健康人群或患病人群脑功能变化与个体行为评分之间的关系成为可能,也为今后的老化进程预测与相关疾病诊治提供了潜在的帮助。进一步,相比于传统的静息态fMRI研究,自然情景范式刺激(如观看电影状态)的fMRI数据为研究大脑如何对复杂的日常事物做出准确反应提供了新的视角[8]。与静息态不同,这种持续性的自然情景刺激显示了大脑皮质区域之间的耦合变化和功能连接波动增加[9]。研究表明,在看电影期间,大脑活动的同步性存在显著的个体差异[10],这种个体差异更有利于预测模型的构建,以帮助我们深入理解大脑功能连接模式与行为之间的关联,揭示脑功能机制。
连接组学预测模型(connectome predictive model,CPM)是一种利用全脑功能连接模型预测个体功能和行为的模型。具体来说,CPM使用全脑功能连接数据作为输入,然后选择一些相关连接作为特征来预测个体特定的行为评分或真实年龄[1]。通常,个体行为评分与CPM预测得分之间的皮尔逊相关一般在0.2到0.5之间[11]。例如,FINN等研究静息态功能连接以预测流体智力时,预测值和实际值之间的皮尔逊相关系数为0.5[6].GREENE et al[7]发现,工作记忆任务中利用特征提取后的功能连接预测的流体智力和真实数值之间的皮尔逊相关在HCP和PNC数据集中分别为0.325和0.351,而相应的静息态结果分别为0.172和0.196.然而,CPM仍然存在一些缺陷,如:过度依赖特征选择,行为数据不服从高斯分布、功能连接与行为评分无显著相关从而导致特征选择失败;不同训练集中功能连接的低重叠导致模型训练失败[11]以及不同的感兴趣区域regions of interest,ROI)和基于体素的功能连接导致预测结果的波动[1]。因此,需要从提高提取复杂特征能力和自动特征学习两个方面对预测模型进行改进。
近些年,深度学习在fMRI研究中取得了很好的发展,其自动特征学习、优于传统方法的分类预测性能使得真实年龄预测[5]、疾病分类[12]、深度挖掘脑功能信息[13]取得了进一步的发展。因此,本研究基于深度学习提出集成深度学习模型,利用个体局部功能连接来预测流体智力:即通过空间自编码机深度挖掘大脑局部功能连接模式并将集成学习与深层神经网络结合起来对个体的流体智力评分进行预测。此外,本研究还对特征可解释性进行了探索。
1 实验数据与方法
1.1 数据预处理与局部功能连接计算
本研究采用了剑桥老化与神经科学中心(the Cambridge Center for Ageing and Neuroscience,Cam-CAN)的公开数据集[14]。被试信息如表1所示。其中包含523名18~88岁健康被试(男性319名,女性328名)。被试男女比例保持平等,每10岁约有100名被试,且采集了所有被试在看电影过程中的fMRI数据。经过数据质量控制,在实际分析中共采用509例被试。数据采集程序均遵循赫尔辛基宣言,并已获得英国当地伦理委员会剑桥郡2号研究伦理委员会的批准。被试在扫描仪外执行一组认知任务(有关完整描述,具体实验信息请参阅[14])。在这项研究中,Cattell评分作为流体智力行为指征。
每例被试在fMRI数据记录过程中,将观看一部名为“Bang!You’re Dead”的黑白电影,影片被从30 min缩短到8 min,并覆盖关键情节。在实验前,确保被试不知道影片内容,也从未看过影片。结构磁共振像用MPRAGE序列采集T1加权解剖图像,参数为:tR/tE=2 250 ms/2.99 ms;翻转角度=9°;FOV=256×240×192 mm3;体素大小=1×1×1 mm3.功能磁共振数据通过多次回波和T2加权回波平面成像(EPI)序列获得193个大脑图像。每个大脑图像包含32个轴向切片,每个厚度为3.7 mm,间隙为20%,tR=2 470 ms,五个回波(tE=9.4 ms,21.2 ms,33 ms,45 ms,57 ms),翻转角度=78°,FOV=192×192 mm2,体素大小为3×3×4.44 mm3。扫描时间为8 min 13 s,与电影时长相同。
图像数据使用神经科学信息工具(NIT)[15]进行预处理,主要包括去除前5幅图像、头动校正、时间校正、空间标准化(功能像首先配准至个体结构像,然后利用TPM(tissue probability map)模板标准化到MNI(montreal neurological institute)空间,体素大小为3×3×3 mm3)等。剔除头动较大(平移大于2.5 mm,旋转大于2.5°,平均帧位移大于0.5)和结构图像缺失的被试数据。最后,使用NIT工具包计算了两种局部功能指标:局部功能连接密度(local functional connectivity density,lFCD)[16]和四维时空一致性功能连接(Four-dimensional (spatio-temporal) Consistency of local neural Activities,FOCA)[17]来评估观看电影时的局部大脑功能活动。
1.2 集成深度预测模型
本文提出一种结合深度学习与集成学习的预测模型,重点在于空间自编码机与集成学习。与常规自编码机不同,空间自编码机将人群中大脑一个体素上的lFCD或FOCA值作为一个样本,并将体素的数量作为样本的数量(约70 000).这样,一方面使得进入空间自编码机的样本量尽可能地大,另一方面空间自编码机的隐藏层的输出值为全脑上的lFCD或FOCA空间图,具有可解释性。在预测流程中,受限于样本数量,为了尽可能地避免过拟合以及提高预测效果,本文采用了深层神经网络结合集成学习来预测流体智力。
模型的具体流程如图1所示。
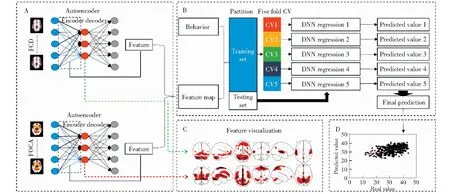
图1 预测模型流程图Fig.1 Pipeline of prediction model
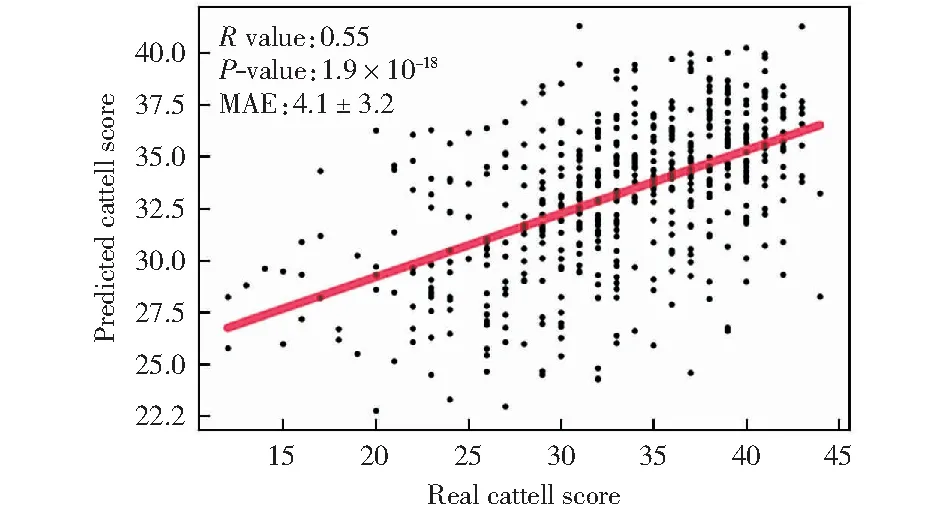
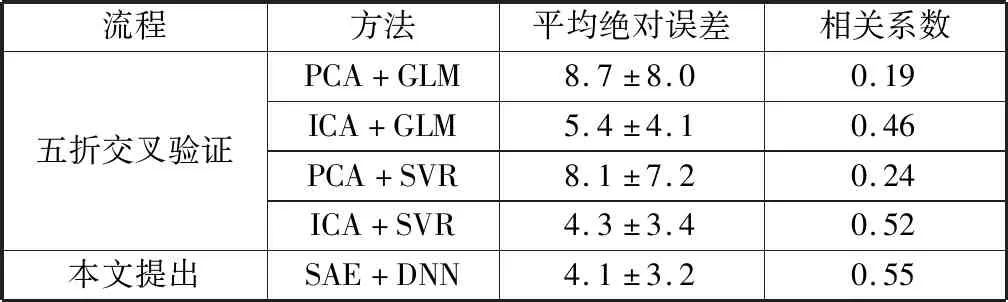
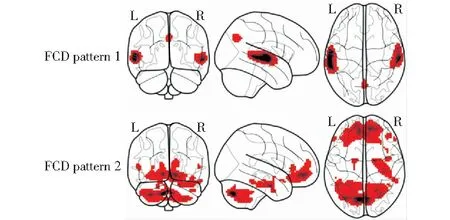
图中A部分使用空间自编码机对lFCD和FOCA进行降维形成特征池:将人群中大脑的每个体素上的值作为样本,并将体素的数量作为样本的数量。通过限制适当的隐藏层节点数(远小于输入维数),实现了全脑体素降维的目的。在训练过程中,基本原则是使输入输出层之间的残差最小。令X=[x1,x2,x3,…,xd]表示lFCD或FOCA一个体素的值;y=[y1,y2,y3,…,yp]表示对应降维后的lFCD或FOCA空间图;z=[z1,z2,z3,…,zd]表示对应的重构数据。空间自编码机的输入维度与输出维度用d表示,与大脑中体素个数相同;隐层节点个数为p(p (1) 在公式(1)中,x(i)是第i个体素上的值,z(i)是对应的重构数据。空间自编码机的代价函数如下: (2) 在公式(2)中,n为全脑体素大小;第一项为人群中体素上的值与重建数据之间的均方误差;第二项为L2范数正则化项(λ1=10-6),它可以通过防止过拟合来提高空间自编码机的泛化能力。 图中B部分将两个空间自编码机的权值组成特征池,用于预测模型的训练和验证:按照集成学习的思想,特征池与标签按4:1的比例随机分为训练集和测试集。通过五折交叉验证将训练集分成5个部分。利用各折互不重复的数据训练相互独立的深层神经网络(DNN)。DNN网络分为4层:第一层为数据输入层,即lFCD和FOCA空间自动编码器中输入层和隐藏层的权重。混合特征的维数为150,包括70个lFCD特征和80个FOCA特征。第二层和第三层是DNN的隐藏层,第二层有100个节点,第三层有50个节点。在输入层和第二层之间加入Dropout层,其参数被设置为0.3.第二层和第三层的非线性激活函数为ReLU函数。最后一层为线性激活层,预测流体智力评分。将这5个模型上最外层测试集的预测值的平均值作为最终预测值。B阶段将重复100次,以测试结果的稳定性。 图中C部分将A步骤所获得的空间自编码机的两个隐藏层的输出值可视化,并解释为lFCD和FOCA空间模式中用于预测的特征重要性。 图中D部分对预测值和真实值进行皮尔逊相关等统计值以评估预测效果。 在本研究中,两个独立的空间自编码机被用于lFCD和FOCA指标的特征提取。在空间自编码机中,需要初始化一些参数,包括损失函数的学习率、L2正则化的学习率、epoch、Batchsize和隐藏层节点数。本研究根据以往经验,将两个空间自编码机的损失函数学习率设为0.000 5,将L2正则项的学习率设为10-5.在优化其他参数之前,空间自编码机的重构误差可以达到0.001以下。同时,经过多次测试,lFCD及其重构误差在45个epoch时保持稳定,而FOCA对应的参数在40个epoch时自编码机得到的重构误差保持稳定。在本研究中,不同的Batchsize初始化对重建误差影响不大,因此,两个空间自动编码器的Batchsize设置为200。值得注意的是,影响重建误差的最重要参数是隐藏层的节点数。经过网格搜索,结果表明,对于lFCD,将隐藏层的节点数设置为70,可以获得稳定且最小的重建误差8.8×10-5.对于FOCA,隐层节点数为80,最小重建误差为1.7×10-3.随着隐藏层节点数的增加,重建误差波动较小。 在本研究中,图1所示的流程用于预测个人的流体智力评分。以被试的预测值与实际值的平均绝对误差(mean absolute error,MAE)和皮尔逊相关系数作为衡量预测结果的指标。DNN预测模型是预测过程的核心。本文所使用的方法得到的流体智力预测值和实际值的MAE为4.1,标准差为3.2,皮尔逊相关值(R值)为0.55,P值为1.9×10-18. 图2 预测的流体智力分数与真实卡特尔分数间的关系Fig.2 Relationship between predicted fluid intelligence score and real cartel score 此外,为了评估本研究提出模型的优势,本研究从降维方法、预测方法和流程设置这3个方面对预测模型进行了比较。在降维方法上,比较了主成分分析法(principal components analysis,PCA)和独立成分分析(independent component correlation algorithm,ICA).在预测方法方面,比较了两种方法:一般线性模型(general linear model,GLM)和支持向量回归(support vector regression,SVR)。在PCA与ICA降维方法中,本文采用MDL方法估计合适的降维维度(即成分个数),其中lFCD为15,FOCA为20;在SVR方法中,其参数为Sklearn工具包中对应模块提供的默认参数。在流程设置方面,选取五折交叉验证的平均结果来评价流体智力评分的预测。如表2所示,PCA+GLM预测平均绝对误差为8.7±8.0,预测值与真实值的皮尔逊相关系数为0.19;ICA+GLM预测平均绝对误差为5.4±4.1,预测值与真实值的皮尔逊相关系数为0.46;PCA+SVR预测平均绝对误差为8.1±7.2,预测值与真实值的皮尔逊相关系数为0.24;ICA+SVR预测平均绝对误差为4.3±3.4,预测值与真实值的皮尔逊相关系数为0.52;而本文提出的方法得到的平均绝对误差为4.1±3.2,预测值与真实值的皮尔逊相关系数为0.55.此外,为了排除预测流体智力中年龄的影响,我们对数据进行了年龄分段预测。具体如下:将数据分为三组,18~45岁为年轻组(207例),45~65岁为中年组(163例),65~88岁为老年组(139例),然后使用论文中同样的方法流程分别对三组数据进行流体智力预测。年轻组中预测分数与真实分数的平均绝对误差为4.21,标准差为3.39,皮尔逊相关为0.54;中年组中预测分数与真实分数的平均绝对误差为4.18,标准差为3.38,皮尔逊相关为0.53;老年组中预测分数与真实分数的平均绝对误差为4.24,标准差为3.37,皮尔逊相关为0.52. 表2 不同方法预测流体智力评分的对比Table 2 Comparation of different prediction methods 空间自编码机经过训练后,其编码器的激活值为对应指标的大脑空间图。经过网格搜索调参,lFCD和FOCA空间自编码机的重建误差趋于稳定和最小,得到了70个lFCD空间图和80个FOCA空间图。空间自编码机隐藏层中每个节点的激活值对应全脑体素在lFCD或FOCA指标中的参与程度(重要性)。激活值越大,参与度和重要性越高。预测流程被重复执行100次,而DNN输入层与隐藏层之间的权值通过二值化可以得到lFCD/FOCA功能模式的参与程度。图3和图4为高选择性(高于50%)lFCD/FOCA空间图。图3中从红色到黑色表示对应区域的重要性正在增加(激活值小于0.6的置为0);图4中从红色到黑色表示对应区域的重要性正在增加(激活值小于0.6的置为0).其重要区域为对应AAL模板中的:颞叶区域(Temporal_Sup_L/R、Temporal_Mid_L/R)、枕叶区域(Calcarine_L/R、Occipital_Mid_L/R Lingual_L/R)、额叶区域(Frontal_Mid_Orb_L/R、Frontal_Inf_Tri_R/L、Frontal_Mid_L/R、Frontal_Inf_Orb_L/R)、基底节网络区域以及小脑区域。 图3 两种lFCD空间图示例Fig.3 Two examples of lFCD spatial maps 图4 两种FOCA空间图示例Fig.4 Two examples of FOCA spatial maps 在空间自编码机训练时,以全脑体素数量作为样本扩大了样本总量,使自编码机能够更全面地检测功能连接性模式。自编码机是一种无监督学习算法,可以有效地从数据中挖掘隐藏的低维表达,然后用于重建原始数据[18]。本研究中,网格搜索被用于设置和优化自编码机的学习速率、Batchsize、epoch、隐藏层节点数和其他参数。lFCD空间自编码机的隐层节点数为70,可以获得稳定且最小的重建误差8.8×10-5;FOCA空间自编码机的隐层节点数为80,最小重建误差为1.7×10-3.随着隐藏层节点数的增加,重建误差波动较小。经过网格搜索后,优化的两个空间自编码机中隐藏层的输出值分别对应lFCD和FOCA在全脑体素上的空间模式图,而对应的输入层到隐藏层之间的权值为用于预测的局部功能连接特征。此外,自编码器提取到的特征是线性和非线性的结合,使得对功能连接的分析更加全面[19]。在这项工作中使用的空间自编码机在最大化数据表达和众多限制(例如,避免恒等转换和冗余特征提取)之间存在折衷。 在之前的研究中,研究者对深度学习模型学习到的特征在符合生物学原理的基础上进行了可视化与解释:DNN输入层与隐藏层之间的权值可解释为具有层次抽象结构的功能连接网络[20]、动态功能连接模式[21]、静息态功能网络[22]等。在本研究中,lFCD和FOCA的两种空间自编码机隐藏层的输出值为与全脑体素维度大小相同的空间连接模式,分别反映了lFCD和FOCA的功能模式。而这种空间模式是冗余的,每一次训练可以得到150个空间图,图3、4分别展示了两种功能指标中出现次数最多的两种空间图。lFCD的空间图展示的重点脑区为双侧颞叶、枕叶以及额叶区域,表明看电影状态下大脑功能活动对声音、视觉刺激的反馈[8]以及高级认知功能的激活[23]。FOCA的空间图展示的重点脑区为顶叶、枕叶区域以及基底节网络及其周边的深部核团区域,表明大脑在观看电影时,视觉、高级认知功能区域的激活[24],而基底节网络可能在此种复杂的自然刺激时起到了各个功能网络间的协调作用[25]。这些特征的解释与先前同类数据的研究结果一致[9,24],表明了新方法能够挖掘到重要的脑功能活动内在信息。 已有研究表明,年龄与流体智力呈反相关关系[11]。为了尽可能地排除年龄对流体智力预测的影响,我们采取了划分年龄段,并针对各个年龄段进行流体智力预测。结果未发现不同的年龄段对流体智力预测产生显著影响。而已发表的类似研究也未对年龄对流体智力预测的影响展开讨论。此外,本研究提出的方法还可以用于多模态信息融合分析,有望为癫痫等脑疾病的前期预测与防治提供重要的影像学依据。 本文基于自编码机及深层神经网络,利用局部功能连接指标,建立了一种新的流体智力的预测模型方法。本文的主要贡献为: 1) 在深层神经网络的基础上充分结合了集成学习,较之神经影响领域最流行的、先进的预测模型-连接组学预测模型(CPM),本文提出的方法其预测误差明显降低。 2) 本文提出了空间自编码机并对其得到的特征可视化与解释方面进行了探索,特征的可视化有效地反映了用于预测流体智力的大脑功能活动空间模式,为我们深入理解年龄相关的大脑功能变化模式提供了重要的信息,具有较好的应用前景。2 结果
2.1 空间自编码机的参数选择
2.2 预测结果
2.3 lFCD与FOCA的空间图及其重要度
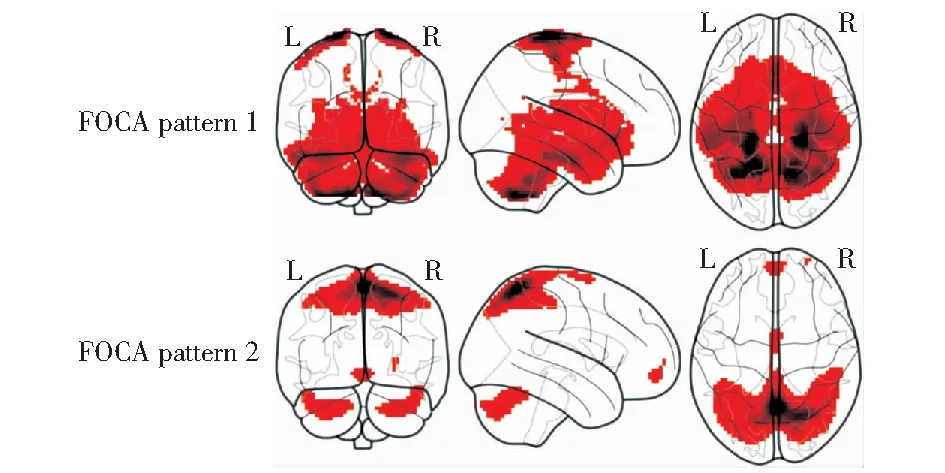
2.4 空间自编码机
2.5 认知功能相关的空间模式
2.6 不足与展望
3 结论

