基于Abaqus的钛合金Ti6Al4V切削仿真与工艺优化

（安徽大学 机械工程系，合肥 230601）

0 引言

探明切削工艺参数对切削力、切削热的影响规律，对实现钛合金材料的高效高质量切削具有重要理论和实践意义。建立切削加工过程仿真模型并进行有限元分析是研究切削加工机理的有效方法之一[1]。徐锦泱等[2]对纤维增强复合材料的切削加工过程进行仿真研究，探究了宏观机械模型、微观机械模型、微宏观机械模型在切削仿真中的应用。郝兆朋等[3]借助有限元仿真对难加工材料镍基高温合金Inconel718切屑形成过程进行分析。李尧等[4]对合金钢30CrMnSiA切削过程进行仿真，发现切削力随刀具前角、主轴转速的增大而先增大后减小。陆涛等[5]对钛合金Ti6Al4V切削过程进行仿真，分析了Ti6Al4V高速切削条件下应力、应变、切削温度的分布规律。

本文基于ABAQUS仿真平台对钛合金Ti6Al4V切削过程进行有限元模拟，采用正交试验设计，极差分析和方差分析方法，研究刀具前角、切削深度、切削速度对切削力和切削温度的影响规律，以期获得钛合金Ti6Al4V切削加工最佳的工艺因素水平。

1 切削仿真模型建立

1.1 几何模型

工件几何模型包含切屑层、连接层和基体三部分，长度均为12mm。切屑层厚度与切削深度相同，连接层、基体厚度分别为0.02mm和3.6mm。刀具几何模型刀尖圆弧半径为0.02mm，刀具前角γ为所研究工艺参数，后角为ξ=6°。切削仿真几何模型如图1所示。

1.2 初始条件和控制方程

图1 工件、刀具装配图

根据工件在机床中的装夹实际情况，约束材料基体左侧和底部边线的自由度；假定刀具为解析刚体，保留其沿水平方向运动的自由度，其速度等于切削速度vc；工件、刀具平面应力应变厚度（z方向）为0.2mm；初始温度设置为室温20℃；接触副为切屑层右侧、顶部与刀具，切屑层、刀具之间的摩擦符合库仑摩擦定律，摩擦系数为0.3[6]；连接层失效准则为剪切失效。

材料模型选用Johnson-Cook（JC）本构模型。JC本构将影响流动应力的应变硬化效应、应变率效应与温度效应用连乘的形式联系在一起综合反映变形热力参数之间的数量关系，其表达式如式(1)所示。

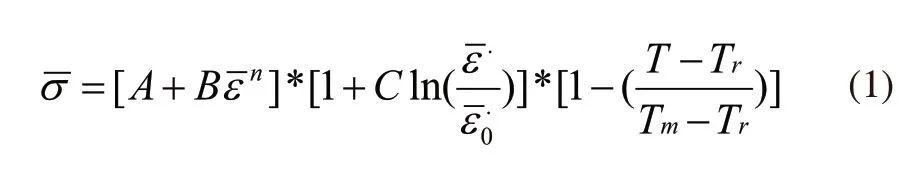
式中，σ为等效应力，A为材料屈服强度，B为应变硬化参数，n为硬化指标，ε为等效塑性应变，C为应变率强化参数，为等效塑性应变率，ε0为材料的参考应变率，m为热软化参数，Tm为材料熔点，Tr为参考温度。

Ti6Al4V材料的JC模型参数如表1所示。工件、刀具材料的物理、力学、热学参数分别如表2、表3所示。

表1 Ti6Al4V材料JC本构参数[7]

1.3 网格控制

工件长度与厚度方向上皆为均匀撒种，长度方向撒种数量皆为300，切屑厚度方向，厚度每增加0.1mm撒种数量增加3，连接层厚度方向不撒种，基体厚度方向撒种数量为10。因为切削过程中的热力作用区多集中于表面层区域，因此，切屑部分网格划分比基体部分网格划分密集。刀具刀尖、右边、上边皆为均匀撒种，刀尖撒种数量为3，右边撒种数量为6，工件网格划分结果如图1所示。

2 仿真试验设计

设计三因素四水平正交试验L16（43），试验方案如表4所示。

3 仿真结果及分析

3.1 仿真结果

图2 钛合金Ti6Al4V切削过程

表2 Ti6Al4V材料的物理、力学、热学参数[8]

表3 刀具材料的物理、力学、热学参数[6]

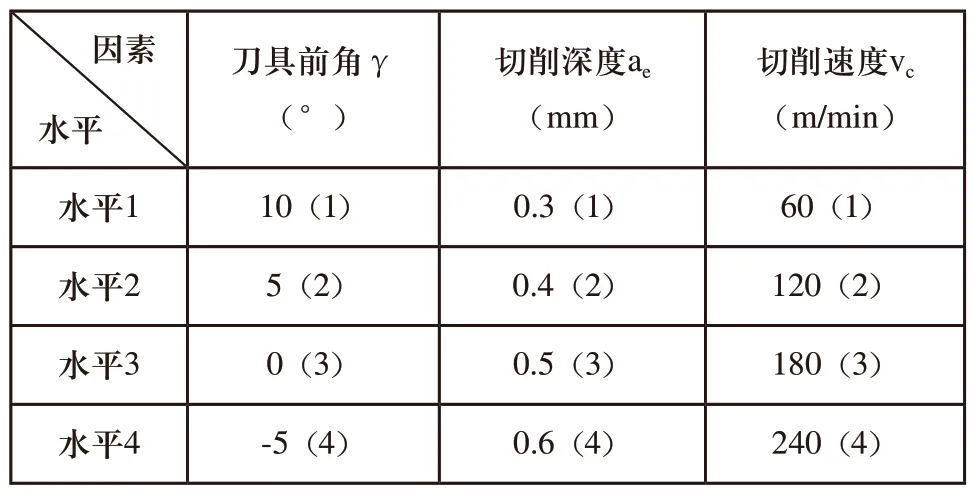
表4 切削仿真L16（43）正交试验表

图2所示为钛合金Ti6Al4V切削过程等效应力和切削温度典型分布云图。由等效应力云图看出，在第一变形区等效应力最大，第二、第三切削变形区等效应力相对较小。由切削温度分布云图可知，切屑形成过程中工件材料剧烈的塑性变形导致切削第一变形区温度最高。

根据牛顿第三定律，切削力与刀具参考点的作用力等大反向，故由刀具参考点输出切削仿真切削运动方向切削分力Fc、垂直切削运动方向切削分力Fp、切削合力Fs，并求得切削分力与切削合力在波动稳定区域的平均值，切削温度T提取工件网格单元在切削过程中的最大值。试验结果如表5所示。

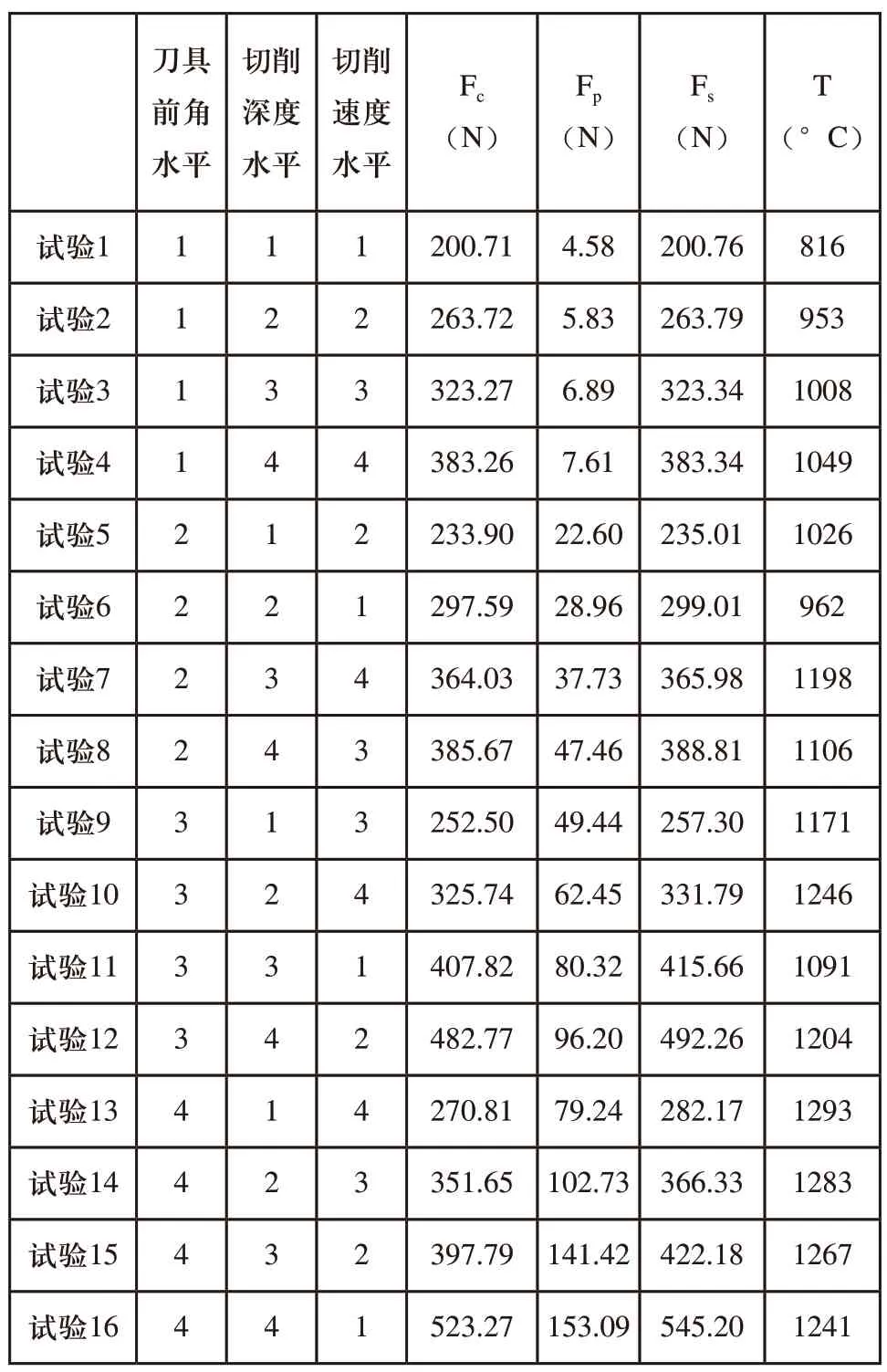
表5 Ti6Al4V切削力和切削温度仿真试验结果

3.2 结果分析

3.2.1 极差分析

极差分析可以使复杂的多因素数据处理问题转化为简单的单因素数据处理问题，计算方法如式(2)～式(4)所示。

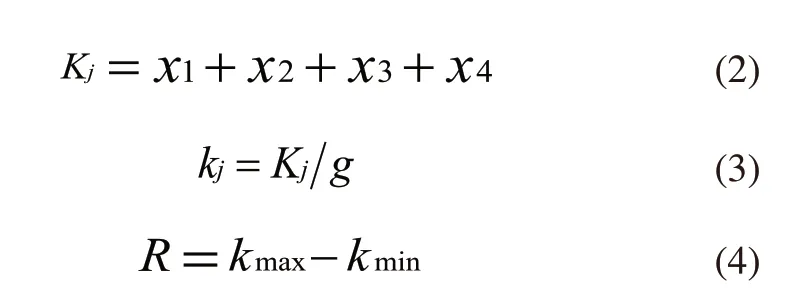
式中，Kj为所研究因素同等水平条件下对应的试验数据之和（j为水平代号），x1、x2、x3、x4为所研究因素同等水平条件下对应的试验数据，kj为所研究因素同等水平条件下对应的试验数据平均值，g为水平重复数，R为极差，kmax为所研究因素的kj最大值，kmin为所研究因素的kj最小值。经过计算，得到切削分力Fc、Fp，切削合力Fs和切削温度T的极差值如表6～表9所示。

表6 切削分力Fc极差分析表

表7 切削分力Fp极差分析表

表8 切削合力Fs极差分析表

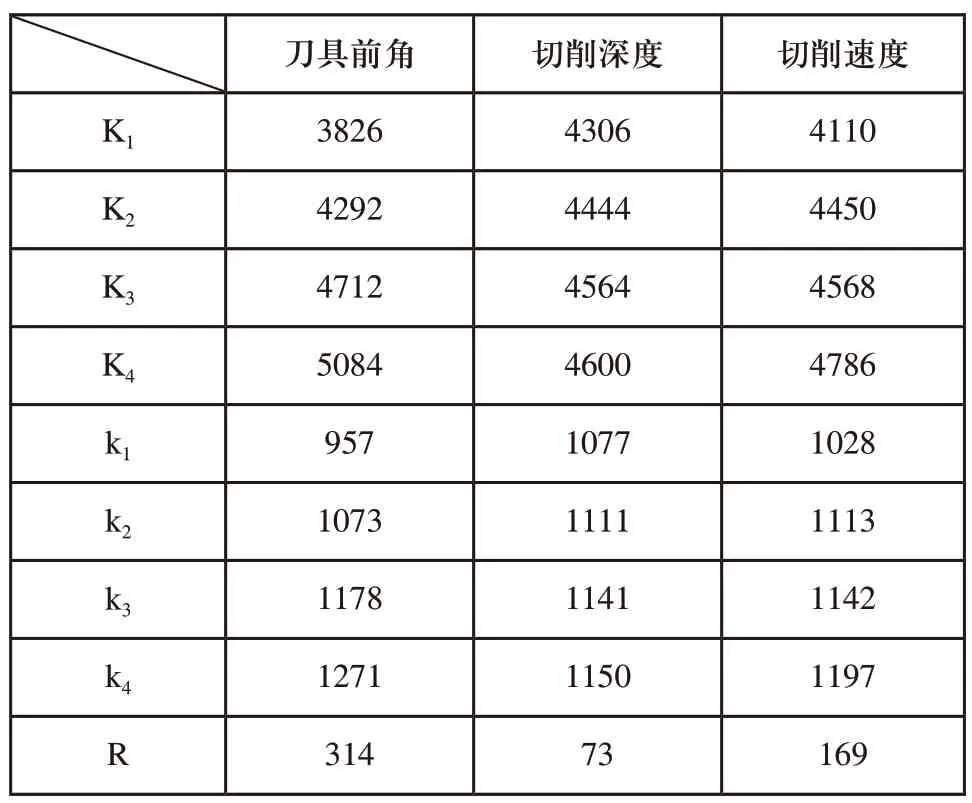
表9 切削温度T极差分析表

由极差分析表可知，切削深度是影响切削分力Fc和切削合力Fs的主要因素；刀具前角是影响切削分力Fp和切削温度T的主要因素。切削分力Fc、Fp，切削合力Fs和切削温度T与切削工艺参数的响应关系如图3～图6所示。

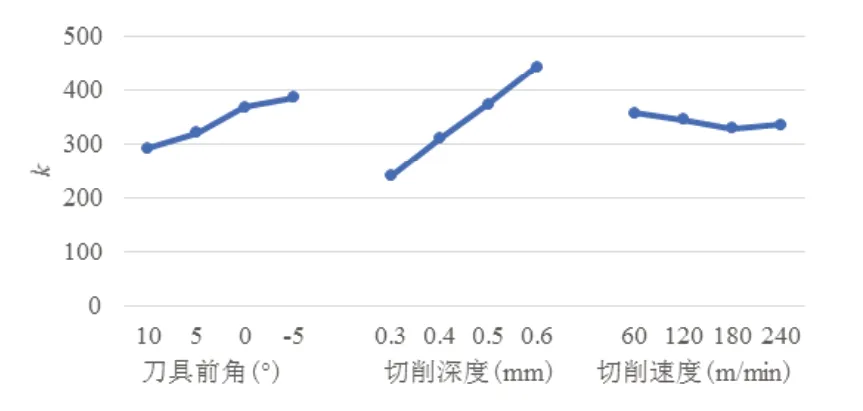
图3 Fc与工艺参数之间的响应关系

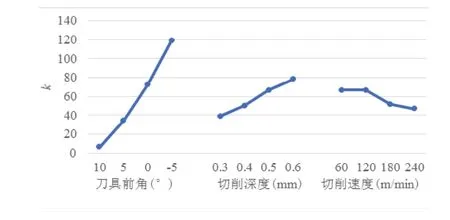
图4 Fp与工艺参数之间的响应关系

图5 Fs与工艺参数之间的响应关系

图6 T与工艺参数之间的响应关系

刀具前角为10°，切削深度为0.3mm，切削速度为180m/min时，切削分力Fc最小；刀具前角为10°，切削深度为0.3mm，切削速度为240m/min时切削分力Fp最小；刀具前角为10°，切削深度为0.3mm，切削速度为180m/min时切削合力Fs，最小；刀具前角为10°，切削深度为0.3mm，切削速度为60m/min时切削温度T最低。对于Fc、Fp、Fs、T四个指标，刀具前角皆以10°为最佳水平，且数值皆随刀具前角减小而增大，切削深度皆以0.3mm为最佳水平，且数值皆随切削深度增大而增大；切削速度对于不同指标影响不同，对于指标Fc、Fs，数值随切削速度增大而先减小后增大，对于指标Fp，数值随切削速度增大而减小，对于指标T，数值随切削速度增大而增大。

3.2.2 方差分析

采用方差分析法可给出误差大小的估计及指出因子的显著性。判断偏差平方和与误差是否相同采用F检验，比较Fy值和所选显著性水平α对应的临界值Fa，并判断该因素是否有显著性的影响程度。对于Fy＞F0.01，表示在α=0.01水平上显著，因素影响高度显著，记为“***”；对于F0.01≥Fy＞F0.05，表示在α=0.05水平上显著，因素影响显著，记为“**”；对于F0.05≥Fy＞F0.1，表示在α=0.1水平上显著，因素影响较显著，记为“*”；对于F0.1≥F＞F0.25，表示在α=0.25水平上显著，因素有影响，记为“-”；对于Fy＜F0.25，称该因素不显著，对所测指标看不出影响，不作记号。计算结果如表10～表13所示。

对于切削运动方向切削分力Fc，FA为11.709，FB为49.091，FC近似为0，由于FB＞FA＞F0.01（3，6）＞＞FC，因此刀具前角和切削深度都属于影响高度显著的因素，且切削深度因素的显著度更高，而切削速度因素影响较小；对于垂直切削运动方向切削分力Fp，FA为22.754，FB为2.622，FC近似为0，由于FA＞F0.01（3，6），F0.1（3，6）＞FB＞F0.25（3，6），因此刀具前角因素的影响高度显著，切削深度因素有影响，而切削速度因素影响较小；对于切削合力Fs，FA为13.19FB为41.973，FC近似为0，由于FB＞FA＞F0.01（3，6）＞FC，因此刀具前角和切削深度都属于影响高度显著的因素，且切削深度因素的显著度更高，而切削速度因素影响较小；对于切削温度T，FA为16.631，FB近似为0，FC为4.511，因FA＞F0.01（3，6），F0.05（3，6）＞FC＞F0.1（3，6），表明刀具前角因素的影响高度显著，切削速度因素影响较显著，而切削深度因素影响较小。

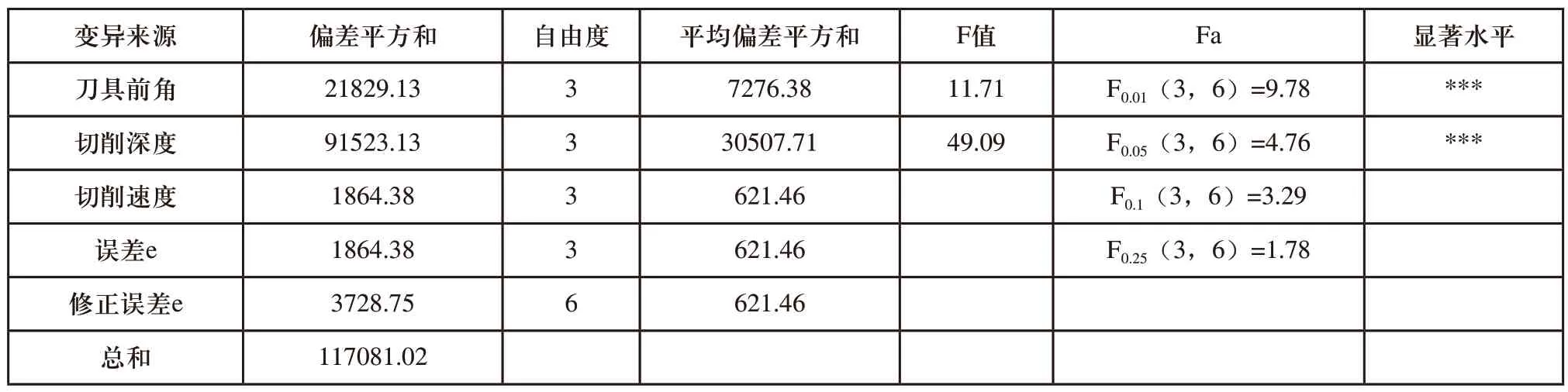
表10 切削运动方向切削分力Fc方差分析表

表11 垂直切削运动方向切削分力Fp方差分析表

表12 切削仿真切削合力Fs方差分析表

表13 切削温度T方差分析表

4 结语

基于Abaqus软件对Ti6Al4V切削过程进行仿真，设计正交实验，借助极差分析与方差分析方法，探究了刀具前角、切削深度、切削速度对工件切削力和切削温度的影响规律，结论如下：

1）刀具前角对切削力与切削温度影响高度显著，当刀具前角为负前角时，切削力与切削温度大大增加。刀具为正前角时，随刀具前角增大，切削力与切削温度有所减小；

2）切削深度对切削力影响高度显著，对切削温度影响不大，随着切削深度的增加，切削力与切削温度都有所增加；

3）切削速度对切削温度影响高度显著，切削温度随切削速度的增加而增加；切削速度对切削力影响不大，在高速切削条件下，当切削速度小于180m/min时，切削力随切削速度增大而减小，当切削速度大于180m/min时，切削力随切削速度增大而增大。