c-空间范畴的一个Cartesian闭满子范畴

车铭静， 寇 辉

（四川大学 数学学院， 四川 成都610064）

1 预备知识

c-空间是由Erné［1-2］提出的一类特殊的拓扑空间，该空间的特征是其拓扑作为完备格是完全分配格.domain理论是研究函数式程序指称语义的数学工具，典型特征是序理论、拓扑学及计算机科学相互 交 叉 融 合［3-6］， 其 主 要 对 象 是 连 续domain［7-8］.每个连续 domain的Scott拓扑恰好是完全分配格［3］，因此c-空间是连续domain这一重要概念的推广.很多作者已对这一空间进行了研究［1，9-11］，但很少有关于 c-空间范畴性质方面的研究.本文通过逼近的方式刻画了c-空间，并定义一类特殊的c-空间，称之为并半格c-空间，该结构是对domain理论中连续格的推广.特别地，本文借助文献［12］中定向空间的概念，运用c-空间的逼近式刻画，证明由所有并半格c-空间及连续映射构成的范畴是c-空间范畴的Cartesian闭满子范畴.

先介绍需要用到的基本知识［7，13-14］.设P是一个非空集合，≤是P上的关系.称≤是P上的偏序，若≤满足自反、传递和反对称性.此时，称（P，≤）是一个偏序集，在关系≤明确的时候，简记为P.设A是偏序集（P，≤）的一个非空子集，记

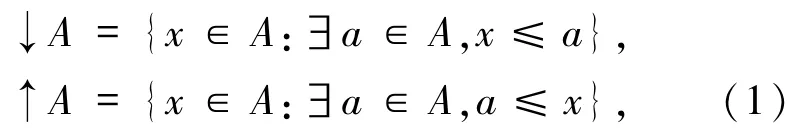
且↑x和↓x分别表示↑｛x｝和↓｛x｝.一个非空子集A⊆P称为是定向的，若任给x，y∈A，存在z∈A，使得z∈↑x∩↑y.称x∈A是A的上确界，如果x是A的一个上界并且小于或等于A的任意上界；特别地，记上确界x＝sup A或者x＝∨A.若偏序集的每个定向子集都有上确界，则成为定向完备偏序集，简称为dcpo.

设P是一个偏序集.一个子集U⊆P称为Scott开集，若对任意定向集D⊆P，∨D存在且∨D∈U意味着D∪U≠Ø.偏序集P的所有Scott开集构成一个拓扑，称为Scott拓扑并记为σ（P）.

接下来介绍T0空间的特殊化序.设X是一个T0拓扑空间，其拓扑通常记为 O（X）.设 A是X的子集，记A为A的闭包，A°为A的内部.X上的特殊化序定义如下：

显然，T0空间的特殊化序是偏序，且对于任意开集U⊆X，U＝↑U，↓x＝x¯，T0空间之间的连续映射保持特殊化序.

若无特殊说明，T0空间总是看成关于特殊化序的偏序集，其上关于序理论的概念，比如上集、下集、定向集等都由特殊化序定义.

定义1.1设X是一个拓扑空间，称映射ξ：J→X为X的一个网，若J是一个定向集.通常简记网为（xj）或（xj）j∈J.任给 x∈X，称网（xj）关于拓扑O（X）收敛到 x，记为（xj）→x或 lim（xj）≡x，如果（xj）终在x的每个开领域中.

显然，T0空间X的每个定向子集D⊆X都可被看成一个网，其子标集就是D自己.由上述定义，定向集D收敛到x（记为D→x或者limD≡x），当且仅当x的每个开领域交D不等于空集.容易验证，∀x，y∈X，xy当且仅当｛y｝→x.令 D（X） ＝｛（D，x）：x∈X，D是 X的定向子集并且 D→x｝.

接下来介绍一类特殊的T0空间.

定义1.2［12］设X是一个T0的拓扑空间.

1）一个子集U⊆X称为定向开集，若任给（D，x）∈D（X），x∈U⇒D∩U≠Ø.记 X的所有定向开集组成的集族为 d（X）.显然，O（X）⊆d（X）.

2）称T0空间X是定向空间，如果每个定向开集都是X中的开集，等价地，d（X）＝O（X）.总把定向空间X上的拓扑记为d（X）.

注 1.31） T0拓扑空间的所有定向开集组成一个拓扑，赋予该拓扑则是一个定向空间［12］.

2）每个偏序集赋予Scott拓扑是一个定向空间［12］.因此，定向空间是比 domain理论的基本结构dcpo更一般的模型.

3）定向空间等价于文献［15］中的monotone determined space.

设X、Y是2个T0空间.函数f：X→Y称为定向连续，如果它是单调的并且保持X的所有定向集的极限； 等 价 地， （ D， x） ∈ D（X） ⇒ （f（D），f（x））∈D（Y）.

引理 1.4［12］设 X、Y是 2个T0空间，函数f：X→Y是 X、Y之间的映射.

1）映射 f定向连续当且仅当∀U∈d（Y），f-1（U）∈d（X）.

2）若X、Y是定向空间，则映射f连续当且仅当它是定向连续的.

记范畴DTop表示以所有定向空间为对象、以所有（定向）连续函数为态射构成的范畴.文献［12］证明范畴 DTop是T0空间范畴的余反射子范畴.

设X、Y是2个定向空间.记X×Y为集合X、Y的笛卡尔乘积.根据X、Y的特殊化序，定义该乘积上一个自然的偏序如下：

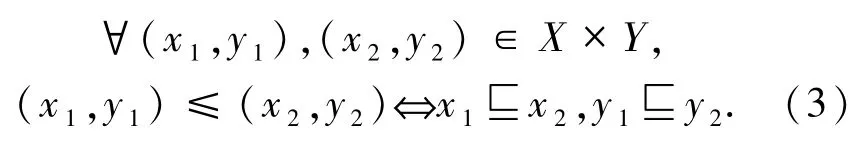
特别地，称该序为X×Y上的点态序.文献［12］在X×Y上定义一个拓扑空间X⊗Y如下：

1） X⊗Y承载集就是X×Y；

2） X⊗Y的拓扑以如下方式生成：任给≤-定向集 D⊆X×Y及（x，y）∈X×Y，记 D⇒（x，y）表示π1D→x且π2D→y.子集U⊆X×Y是开的当且仅当对任意按上述方式定义的极限 D⇒（x，y），（x，y）∈U⇒D∩U≠Ø.

令O（X×Y）表示 X和 Y的乘积拓扑，令O（X⊗Y）表示按上述方式生成的拓扑.容易看出，O（X×Y）⊆O（X⊗Y）恒成立，且由乘积拓扑O（X×Y）诱导的序就是点态序.

定理 1.5［12］对任意 2个定向空间X和Y，X⊗Y是一个定向空间满足：

2） 任给定向集D⊆X⊗Y及（x，y）∈X⊗Y，D→（x，y）当且仅当D⇒（x，y）；

3） X⊗Y是范畴DTop中X和Y的范畴乘积.

以后，定向空间X⊗Y记为d（X×Y）.

设 X、Y是2个定向空间.令YX表示X、Y之间的所有（定向）连续函数之集.YX上存在一个自然的诱导序：

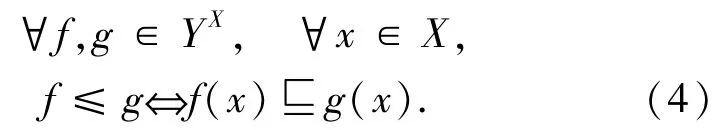
该序称为YX上的点态序.文献［12］中在YX上以如下方式定义了一个拓扑空间［X→Y］：

1） ［X→Y］的承载集就是 YX；

2） ［X→Y］的拓扑按如下方式生成：子集U⊆YX是开集当且仅当对任意≤-定向子集｛fi：i∈I｝⊆ YX及f∈ U， 若 对 任 意x∈ X，（fi（x））i∈I→f（x），则有U∩｛fi：i∈I｝≠Ø.

记O（YX）表示按上述方式定义的所有开集之集并令［X→Y］＝（YX，O（YX））.

引理 1.6［12］任给2个定向空间X和Y，［X→Y］是一个定向空间且满足

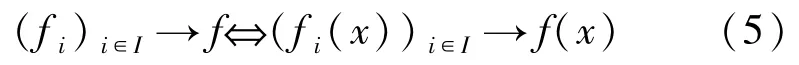
对所有x∈X成立.任给子集U⊆ ［X→Y］，U∈O（YX）当且仅当对任意-定向子集｛fi：i∈I｝⊆YX，若（fi）i∈I→f且 f∈U，则存在 i0∈I使得fi0∈U.

从现在开始，称空间［X→Y］为定向空间X和Y的函数空间，并记d［X→Y］＝O（YX）.特别地，文献［12］证明了如下重要结果.

定理1.7定向空间范畴DTop是Cartesian闭范畴，其中，任意2个定向空间的范畴乘积及对应指数对象方别是X⊗Y和［X→Y］.

因此，定向空间范畴满足作为函数式程序指称语义数学模型的基本条件，是对domain理论基本结构的推广.

2 c-空间及其相关刻画

连续domain 是domain理论中最重要的结构，其核心特征是每个元能够被逼近［7］.Erne［1-2］注意到连续domain关于Scott拓扑的性质，提出了连续domain的一种推广结构，称之为c-空间.其具体定义如下.

定义2.1设X是一个T0拓扑空间.称X是一个c-空间，如果任给x∈X及x的开邻域U，存在y∈U使得 x∈（↑y）°；等价地，｛（↑y）°：y∈X｝是拓扑空间X的一个基.

定理 2.2［1-2］一个 T0拓扑空间X是一个c-空间当且仅当其拓扑O（X）是一个完全分配格.

由于每个连续domain的Scott拓扑是完全分配格［7］，所以连续 domain关于Scott拓扑是一个c-空间.因此，c-空间是连续domain的推广，并有大量学者研究了该空间.比如，Ershov［10-11］在1993年和1997年以α-空间的名称研究了c-空间，Keimel［9］于 2008年把c-空间与拓扑锥的概念相结合提出c-锥概念.

事实上，下面将借助定向空间的性质对c-空间给出类似于连续domain的刻画.

命题2.3每个c-空间都是定向空间.

证明设U⊆X是定向开集.下证U是X的开集.任给 x∈U，令 A＝｛y∈X：x∈（↑y）°｝.由 c-空间的定义知，A是定向的且A→x.因为U是定向开集，由定义1.2的 1），存在 a∈D∩U使得 x∈（↑a）°⊆U，所以U是X中的开集.这表明X的所有定向开集都是开集，因此X是定向空间，见定义1.2的2）.

设X是一个定向空间，∀x，y∈X.称x逼近y，记x≪y，如果下述条件成立：对任意定向集D⊆X，若D→y，则存在d∈D，使得xd.对任意 x∈X，记

注2.4由于每个偏序集赋予Scott拓扑是定向空间，上述逼近关系在Scott拓扑下等于偏序集上的way-below关系.

下面关于逼近关系的性质是显然的.

命题 2.5设 X是一个定向空间，x，y，z，t∈X.则下述2

条成立：

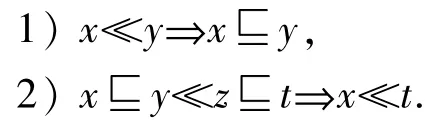
引理2.6设X是一个c-空间，则下列各条成立：

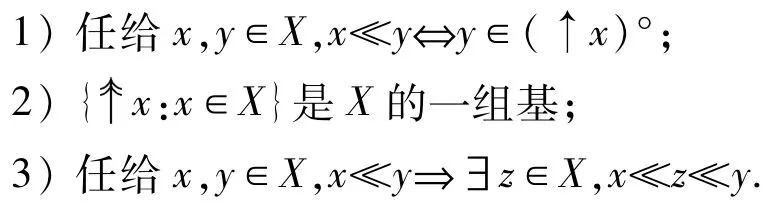
证明1） 设 x，y∈X且 x≪y.令 Ay＝｛a∈X：y∈（↑a）°｝，则由X是c-空间，有 Ay是一个定向集且Ay→y.由逼近关系的定义，存在a∈Ay使得xa.从而，y∈（↑a）°⊆↑a⊆↑x.因此，y∈（↑x）°.反之，设 y∈（↑x）°.任给定向集 D⊆X，若D→y，则 D∪（↑x）°≠Ø.取 d∈D∪（↑x）°，则 xd，从而由逼近关系的定义有x≪y.

引理2.7设X是一个T0空间，则下列各条成立.

1） X是一个c-空间；

证明1）⇒2） 由命题2.3，X是一个定向空间.由引理 2.6，对任意（↑a）°｝.由 c-空间的定义是一个定向集且

2）⇒3） 显然.

3） ⇒1） 首先证明，对任意 a，s∈X，s≪a⇒∃s′∈X，s≪s′≪a.

令 W＝｛z∈X：∃w∈X，z≪w≪a｝，W是一个定向集且W→a.由已知条件非空对所有x∈X成立，因此，W≠Ø.任给 z1，z2∈W，则存在 w1，w2∈X使得 zi≪wi≪a，i＝1，2.由已知条件，存在定向集使得Da→a.由逼近关系的定义，存在b1，b2∈Da使得因为 Da定向且包含于所以存在使得注意到 zi≪b（i＝1，2），由上面相同的理由，存在z≪b使得 z1，z2z.这表明，b∈W且是 z1、z2的上界.因此，W是一个定向集.下证W→a.设V⊆X是a的一个开邻域.由上面的证明，定向集且Da→a.从而存在 c∈V∩Da.再次运用条件3），存在定向集使得Dc→c.从而存在e∈Dc∩V.这表明e∈W∩V，即W→a.由于s≪a，故存在z∈W使得由 W的定义，存在 s′∈X使得 z≪s′≪a.从而，s≪s′≪a.

接下来，设a∈U且U⊆X是a的开邻域.则存在 z′∈W，使得 z′≪a且 z′∈U，从而U.下证是开集即可.由于X是定向空间，即证是定向开集.设D⊆X且由上面的证明，存在y∈X使得z′≪y≪x.从而存在d∈D使得即.命题得证.

推论2.8设X是一个c-空间，则对任意x∈

证明由定理是定向集且由逼近关系的定义，x显然是的一个上界.假设y∈X是的另一个上界，且则 x∈X＼↓y.注意到从而矛盾.

结合推论，当X是一个赋予Scott拓扑的偏序集、dcpo、完备格等，定理就是连续偏序集、连续domain、连续格等结构的定义或者等价刻画［7］.

命题2.9设X是一个c-空间.则对任意定向空间Y，X⊗Y＝X×Y.这里，X×Y表示拓扑乘积.

证明由定理1.5，X⊗Y是定向空间且其特殊化序等于点态序≤.记O（X×Y）表示（拓扑）乘积空间的拓扑.任给 U∈d（X），V∈d（Y）及定向集D⊆X×Y，如果π1D→x∈U且π2D→y∈V，则存在d1∈π1D∩U及 d2∈π2D∩V，从而存在 d3∈π1D及d4∈π2D满足（d1，d4），（d3，d2）∈D.由 D是定向的，存在（d5，d6） ∈D满足（d1，d4），（d3，d2） ≤（d5，d6）.这表明（d5，d6）∈D∩（U×V）.因此，U×V∈d（X×Y），即 O（X×Y）⊆d（X⊗Y）.接下来证明d（X×Y）⊆O（X×Y）.设（x，y）∈W∈d（X⊗Y）.令W（y） ＝｛z∈X：（z，y）∈W｝.则 x∈W（y）.设 D⊆X是一个定向集且 D→z∈W（y）.令 Dy＝｛（d，y）：d∈D｝，则 Dy是 X⊗Y的定向集且 Dy⇒（z，y），从而存在 d∈D，使得（d，y）∈W，即 d∈D∩W（y）.因此，W（y）是x的开邻域.因为X是一个c-空间，故存在 z∈W（y）使得用上面的方法可证 W（z） ＝｛t∈Y：（z，t）∈W｝是 y的开邻域.令任给（a，b）∈U×V，则（z，b）（a，b），且（z，b）∈W，从而（a，b）∈W.这表明（x，y）∈U×V⊆W.因此，d（X×Y）⊆O（X×Y）.命题得证.

推论2.10设X，Y是2个c-空间.则 X×Y是一个c-空间，X⊗Y＝X×Y且对于任意（a，b），（x，y）∈X⊗Y，（a，b）≪（x，y）⇔a≪x，b≪y.这里，X×Y表示拓扑乘积.

证明由命题2.9可知，X⊗Y＝X×Y.任给（x，y）∈W∈d（X×Y），则存在 U∈d（X）及 V∈d（Y）使得（x，y）∈U×V⊆W.因为 X，Y是 c-空间，存在a∈U及b∈V使得 x∈（↑a）°⊆↑a⊆U且y∈（↑b）°⊆↑b⊆V.从而，（x，y）∈（↑a）°×（↑b）°⊆（↑（a，b））°⊆↑a ×↑b＝↑（a，b）⊆U×V⊆W.由定义1.2的2），X×Y是一个c-空间.

记CTop表示以所有c-空间为对象、以所有（定向）连续函数为态射的范畴.则定理1.7、命题2.3及推论2.10，下述结论成立.

定理2.11CTop是定向空间范畴DTop关于有限范畴乘积封闭的满子范畴.

3 c-空间范畴的一个Cartesian闭子范畴

由于每个连续偏序集赋予Scott拓扑都是c-空间，所以c-空间是对domain理论［7］的重要对象—连续domain的推广.在domain理论中，连续格关于Scott连续映射都构成连续domain 的Cartesian闭满子范畴［7］.本节将定义一类特殊的的 c-空间，称之为并半格c-空间，该结构是连续格的推广.证明所有并半格c-空间及连续映射构成的范畴是c-空间范畴CTop的Cartesian闭满子范畴.

设P是一个偏序集，a，b∈P.若a、b在P有上确界，则记该上确界为a∨b.设A⊆P且a与A中的每个元素有上确界，则记a∨A＝｛a∨b：b∈A｝.

定义3.1一个定向空间X称为并半格定向空间，如果它满足以下条件：

1） X有最小元（记为0X）；

2） 任给 a，b∈X，a∨b存在；

3） 任给定向集 D⊆X及 a，b∈X，若 D→a，则b∨D→b∨a.

此时，当X是一个c-空间时，则称X是一个并半格c-空间.

一般而言，并半格不要求有最小元，为本文下面的讨论，特地要求并半格定向空间具有最小元.

例 3.21）每个赋予Scott拓扑的完备格（连续格，见文献［7］）的定义，是一个并半格定向空间（并半格c-空间）.其逆命题并不成立（见下例）.

2） X＝［0，1］∩Q，这里Q表示有理数集.令

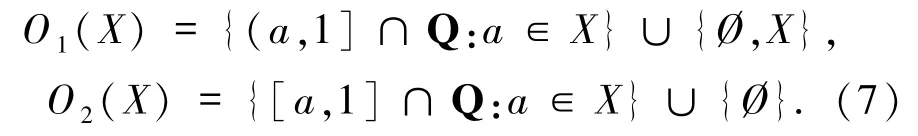
容易验证，（X，O1（X））和（X，O2（X））都是并半格c-空间，其特殊化序就是通常的大小关系.值得注意的是，X显然不是完备格且第二个拓扑不等于Scott拓扑.

记SCTop表示以所有并半格c-空间为对象、以所有连续函数为态射的范畴.则连续格范畴是SCTop的真子范畴.

命题3.3若 X、Y是2个并半格c-空间，则X×Y是一个并半格c-空间.

证明由推论2.10，X×Y是一个c-空间.只需证明它是并半格.令0X⊗Y＝（0X，0Y），则它是 X×Y的最小元.任给∀（x1，y1），（x2，y2）∈X⊗Y，由并半格定向空间的定义，x1∨x2和y1∨y2存在.显然，（x1，y1）∨（x2，y2） ＝（x1∨x2，y1∨y2）.现在设 D为X⊗Y的定向子集，且 D→（a，b）.则π1D→a且π2D→b.任给（x，y）∈X⊗Y，由 X、Y为并半格定向空间可得 x∨π1D→x∨a，y∨π2D→y∨b.由

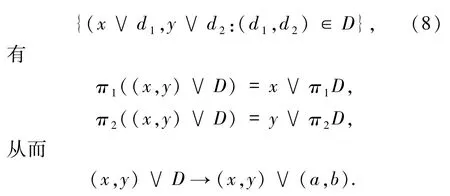
接下来考虑c-空间之间的函数空间.设X、Y是2个c-空间且Y具有最小元0Y，a∈X，b∈Y.定义映射 a↘b：X→Y如下：

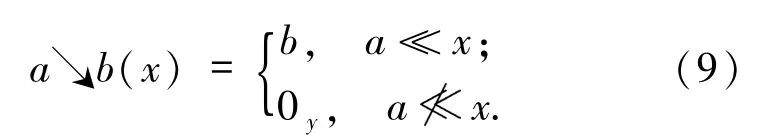
该函数称为步函数（在domain理论中称为步函数［7］）.

引理3.4步函数是连续的.

证明a↘b：X→Y的定义如上.单调性是显然的.设D⊆X是一个定向集且 D→x∈X.则 a↘b（D）是定向的.若 a≪x，则 a↘b（x） ＝b.由引理2.6，存在a1∈X使得a≪a1≪x.从而存在d∈D满足a1d.再由命题 2.5，有 a≪d，从而 a↘b（d） ＝b.这表明，b的任何开邻域交a↘b（D）不等于空集.因此，a↘b（D）→b＝a↘b（x）.若ax，a↘b（x） ＝0y.a↘b（D）→0y显然成立.步函数的连续性得证.

命题3.5设f：X→Y是 c-空间 X，Y间的连续函数，Y有最小元0X.x，a∈X，y，b∈Y满足：xa，b≪y且 f（x） ＝y.则在函数空间［X→Y］中，步函数a↘b≪f.

证明由引理3.4，a↘b∈［X→Y］.设D＝｛fi：i∈I｝是函数空间［X→Y］的一个定向集且D→f.由引理 1.6，（fi（x））i∈I→f（x）成立.由 b≪y＝f（x），存在ix∈I使得任给 z∈X，若 a≪z，则若则显然成立.因此从而，a↘b≪f成立.

定理3.6设X、Y是2个并半格c-空间，则函数空间［X→Y］也是一个并半格c-空间.

证明由引理1.6，［X→Y］是一个定向空间.定义映射0［X→Y］：X→Y如下：∀x∈X，0［X→Y］（x） ＝0y.显然，0［X→Y］是［X→Y］的最小元.取 f，g∈［X→Y］，定义 f∨g：X→Y如下：

显然，f∨g 是良定义的且保序.设D⊆X是定向的且D→x∈X.则由f和g的连续性，有 f（D）→f（x）和 g（D）→g（x）.由定义3.1，f（D）∨g（x）→f（x）∨g（x）.设 U⊆Y是 f（x）∨g（x）的开邻域.则存在d1∈D使得 f（d1）∨g（x）∈U.同理，由 f（d1）∨g（D）→f（d1）∨g（x），存在 d2∈D使得 f（d1）∨f（d2）∈U.在由D的定向性，存在d∈D使得d1满足d1d，从而 f（d）∨g（d）∈U，即（f∨g）（D）→（f∨g）（x）.因此，f∨g是连续的，从而是f、g在函数空间［X→Y］的上确界.设D＝｛fi：i∈I｝是函数空间［X→Y］的定向集且D→f∈［X→Y］.由引理1.6有

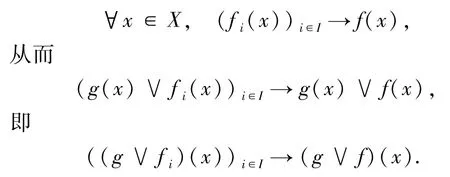
再由引理 1.6，g∨D→g∨f（x）.因此，函数空间［X→Y］是一个并半格定向空间.

接下来证明，函数空间［X→Y］是一个c-空间.设 f∈［X→Y］.令

注意到X和Y都有最小元，A≠Ø.任给非空有限集F⊆A，不妨设 F＝｛（a1，b1），（a2，b2），…，（an，bn）｝，定义 fF：X→Y如下：

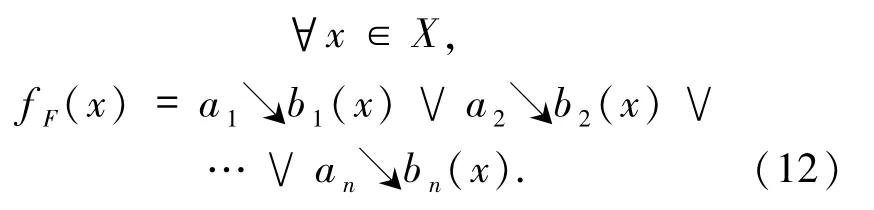
由上面的证明知，fF∈［X→Y］且是诸步函数的上确界.下证 fF≪f.设D＝｛fi：i∈I｝是函数空间［X→Y］的一个定向集且D→f.由命题3.5知，ai↘bi≪f，1≤i≤n.故对每个 i存在 fi∈D使得由D的定向性，存在g∈D使得从而因此，fF≪f.令

则B是一个定向集，且B⊆f.由定理2.7，只需证明B→f.由引理1.6，只需证明

由引理2.6，只需证明，∀b≪f（x），存在 Fb∈B使得 b≪fFb（ x）.设 b≪f（x），则由引理 2.6，存在 c∈Y满足 b≪c≪f（x）.由定理定向且收敛到 x.因为 f连续，故定向且收敛到 f（x）.从而存在满足 c≪f（d）.令 Fb＝｛（d，c）｝，则 fFb＝d↘c.显然，b≪c＝fFb（x）.

由命题3.3及上述定理可知，并半格c-空间范畴SCTop作为c-空间范畴CTop的满子范畴关于有限范畴乘积及函数空间是封闭的.注意到c-空间范畴CTop是定向空间范畴DTop的满子范畴，且由定理1.7，DTop是 Cartesian闭范畴，其范畴乘积及指数对象分别是X⊗Y及［X→Y］.因此，得到本节如下主要结果.

定理3.7并半格c-空间范畴SCTop作为c-空间范畴CTop的Cartesian闭满子范畴.

这一结果表明，c-空间范畴的存在不同于domain

理论的Cartesian闭范畴，可为研究函数式程序语言指称语义提供更一般的数学模型.