交替博弈中两类循环优势系统的动力学行为

刘 静， 刘春燕， 陆征一， 杨 鸣

（1.武警警官学院部队管理系，四川成都610213； 2.四川师范大学数学科学学院，四川成都610066；3.中国科学院成都计算机应用研究所，四川成都610041）

复制系统与 Lotka -Volterra 系统［1］是进化博弈中的 2 个重要模型.1998 年，Sigmund［2］在国际数学家大会（ICM）报告中将Lotka-Volterra系统与复制系统作为2 个主题分别进行了总结，综述了永久生存性、稳定性、异宿环、极限环存在性等一系列结果且说明了两者之间存在等价性.利用两系统的等价性和中心流形定理［3］，杨静等［4］用异于前人的方法得到了三维Lotka -Volterra 系统极限环的存在性，汪芳［5］得到三维复制系统在正平衡点处存在中心或全局稳定的充分必要条件.

进化博弈［6-7］中具有循环优势的博弈是近年来学术研究的热点，其有效地解释了策略的选择和进化.人们发现循环优势博弈不仅能够深入的解释自然选择理论，还能解释物种空间分布复杂性［8］和物种进化［9］.实例表明，物种多样性也可以用循环优势博弈来解释.学者们还不断拓宽着经典的石头-剪刀-布三循环优势博弈的研究，不仅研究了其吸引性理论［10-11］，还将其应用到微观竞争群体［12］和大范围生物群落［13-14］.四物种循环演化博弈［15］也具有与石头-剪刀-布博弈相似的结论，即过快的流动性会破坏系统的生物多样性.而在四循环优势博弈中，还会出现三循环优势博弈中不存在的中性策略对，即存在2 种策略互不入侵的情形.

进化博弈中可考虑同步博弈和交替博弈.同步博弈是指两位参与者同时做决定，而交替博弈是两位参与者先后做决定进行博弈.现在的大多数研究基于同步博弈中较为简单的策略相互博弈展开的，但对交替博弈中更复杂的策略相互博弈所产生的循环优势系统的研究还不丰富.本文将在交替博弈中对新规定下的16 种策略相互博弈产生的三、四循环优势系统的性质展开研究.先给出了基于行为误差的交替博弈在不同成本收益比k 值情形下，具有三、四循环优势的系统的数量，得到了三循环优势系统的完全分类和四循环优势系统的永久生存性；再利用Lotka-Volterra 系统与复制系统的等价性，中心流形定理和实根分离等理论，考虑基于行为误差的交替囚徒困境中，具有四循环优势的系统［S4，S8，S10，S15］的极限环的存在性.

1 三循环优势系统

在双人博弈中参与者Ⅰ和参与者Ⅱ每次博弈都有2 种选择：合作C 或背叛D，博弈中可出现4种状态：（C，C）、（C，D）、（D，C）、（D，D），其对应的收益分别为 R、S、T、P.用 qR、qS、qT、qP来表示上一轮获得收益 R、S、T、P 本轮选择合作的概率.如果只考虑反应规则（qR，qS，qT，qP）的空间，这个单位方形由它的 16 个顶点张成，即由向量（uR，uS，uT，uP）张成，其中 ui取 0 或 1 决定于获得收益 i∈｛R，T，P，S｝后策略选择是背叛还是合作.将这些策略记为 Sj，j ＝0，1，…，15.而（uR，uS，uT，uP）由二进制给出，例如回报者 TFT ＝ （1，0，1，0）表示为 S10.通过文献［16］计算方法可以得到交替囚徒博弈中16种策略相互博弈所对应的收益，见表1 所示.

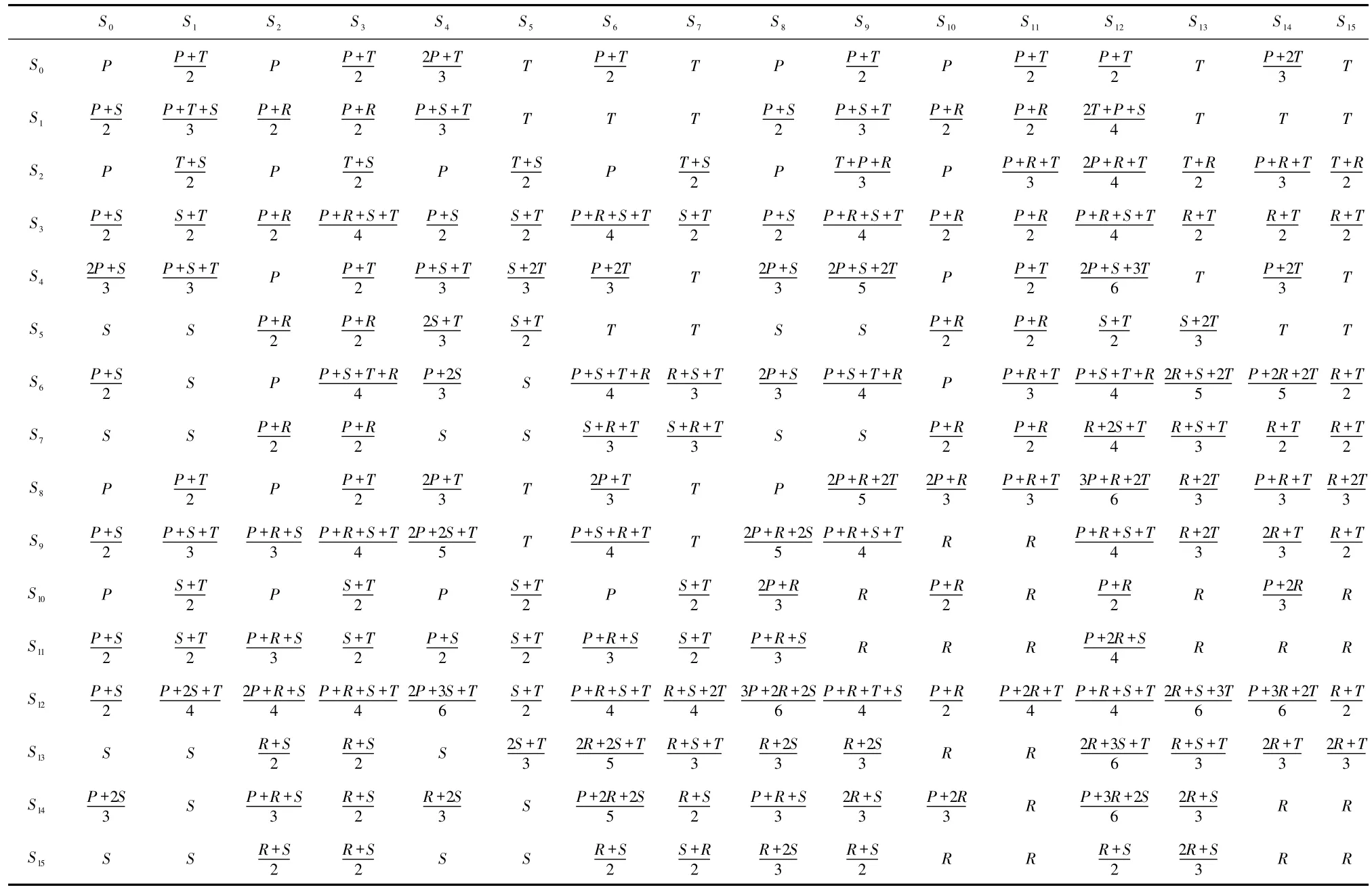
表1 具有行为误差的交替的囚徒困境博弈Tab. 1 Alternating prisoner’s dilemma game with behavioral errors

当支付成本为 c，收益为 b，且 b ＞c时，即

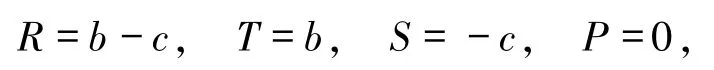
该博弈称捐赠博弈，其收益见文献［16］.由达尔文选择定律可知群体中策略的单位增长率可由（AX）i-X·AX 给出，其中

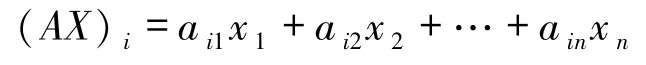
为当群体处于状态 X ＝ （x1，x2，…，xn）时，策略 i的收益，X·AX为群体的平均收益.由此，可得单形

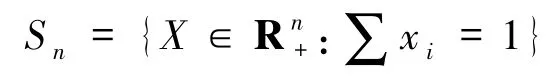
上的复制方程

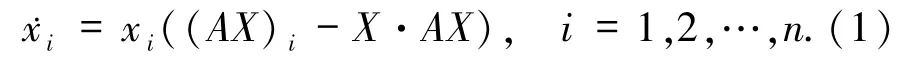
考虑复制系统（1）当 n ＝2 时的情形，其正平衡点

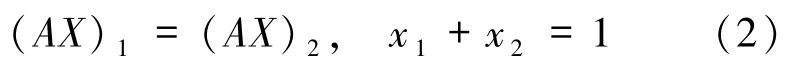
满足 xi＞0（i ＝1，2）的解.又由于收益矩阵添加任意函数 f（x），复制系统（1）不会改变.因此，当只有2 种策略相互博弈时，可假设其收益矩阵A 为如下形式

引理 1［16］在收益矩阵为 A 的系统中，如果a、b 不同时为 0 且 ab≤0 时，则当 a ＞ b 时，策略 x1占优；当 a ＜b时，策略 x2占优.

由引理1 可以得到任意两策略相互博弈的占优情形，为实现对成本收益比的完全分类，根据收益矩阵的特殊性可将 k 分为4 个区间：

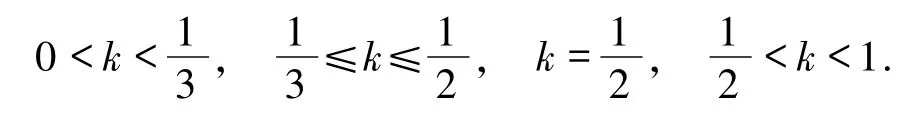
［0，1］，［0，3］，［0，4］，［0，5］，［0，6］，［0，7］，［0，9］，［0，12］，［0，13］，［0，15］，［1，5］，［1，6］，［1，7］，［1，12］，［1，13］，［1，14］，［1，15］，［3，1］，［3，2］，［3，13］，［3，14］，［3，15］，［4，2］，［4，3］，［4，5］，［4，6］，［4，7］，［4，12］，［4，13］，［4，15］，［5，2］，［5，6］，［5，7］，［5，13］，［5，14］，［5，15］，［6，2］，［6，15］，［7，2］，［7，3］，［7，6］，［7，10］，［7，14］，［7，15］，［8，1］，［8，3］，［8，4］，［8，5］，［8，7］，［9，1］，［9，5］，［9，7］，［9，13］，［9，15］，［10，0］，［10，1］，［10，2］，［10，8］，［11，1］，［11，2］，［11，3］，［11，5］，［11，8］，［11，9］，［11，10］，［11，13］，［12，7］，［12，13］，［12，15］，［13，14］，［13，15］，［14，2］，［14，8］，［14，10］，［15，10］.

由此可以得到在具有行为误差的交替捐赠博弈中的16 种策略相互博弈所形成的三循环优势系统与四循环优势系统.

2 三循环优势系统完全分类

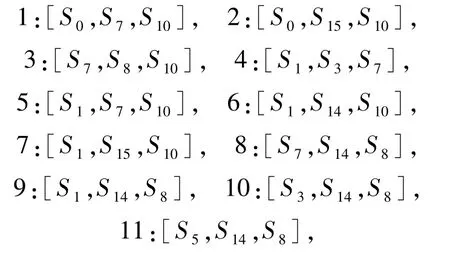
其中，三循环优势系统1、2、3、6 和 7 存在孤立正平衡点.

引理2［5］当复制系统（1）存在正平衡点时，其存在中心的充分必要条件是

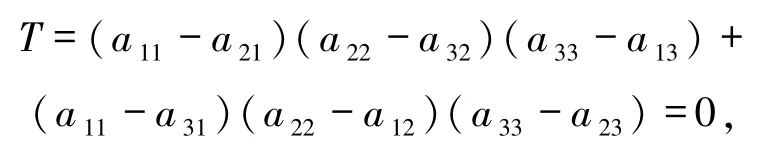
且下列条件之一成立：

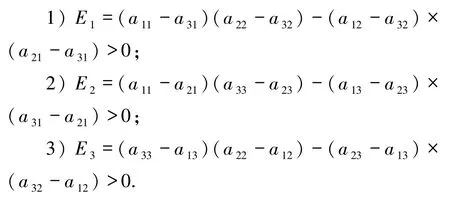
考虑具有行为误差的交替捐赠博弈系统，合作者（ALLC）S15总是提供帮助；背叛者（ALLD）S0，总是不提供帮助；回报者（TFT）S10当且仅当对手上一回合不提供帮助时，本回合不提供帮助.三循环优势系统2 中3 个策略相互博弈具有收益矩阵：

因此，由引理2 知三循环优势系统2 正平衡点处存在中心.

同理，可验证三循环优势系统 8、9、10、11 存在中心.

引理 3［5］当复制系统（1）存在正平衡点，即满足引理2 中的条件1）～3）且

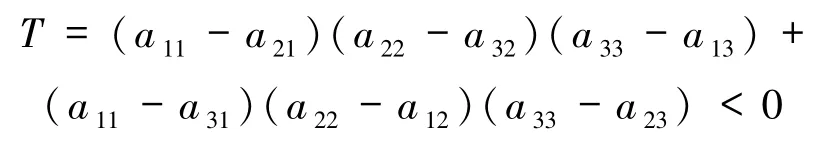
时，该系统全局稳定的充分必要条件为下列条件之一成立：

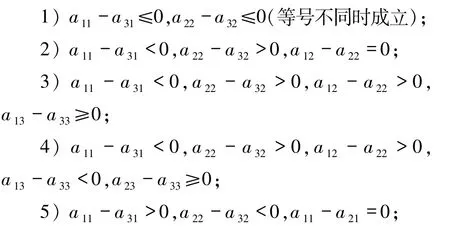
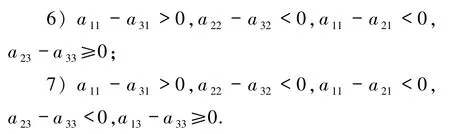
三循环优势系统7 中具有野心（这个策略只有在相互背叛后才合作，一旦遇到傻瓜便都无情的背叛）的只满足于 T 的策略 S1＝（0，0，0，1），与 S10、S15博弈构成三循环优势系统，现讨论其动力学行为.

系统［S1，S10，S15］具有收益矩阵

故三循环优势系统7 满足引理3 中条件6），具有全局稳定性.

保留系统［S1，S10，S15］中的策略 S1与回报者S10，将合作者S15替换成与策略S1恰好完全相反的策略S14（该策略称为“滞后的傻瓜”只有在相互背叛后才选择背叛），三策略组成系统6，此系统仍是三循环优势系统且具有全局稳定性.

具有正平衡点的三优势循环系统，如果其正平衡点不存在中心且非全局稳定，那么其平衡点为不稳定焦点，即三循环优势系统1、3 的正平衡点为不稳定焦点.

三循环优势系统1 具有收益矩阵

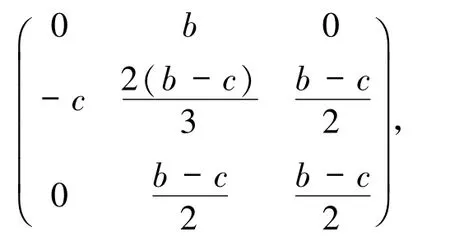
做负变换有收益矩阵

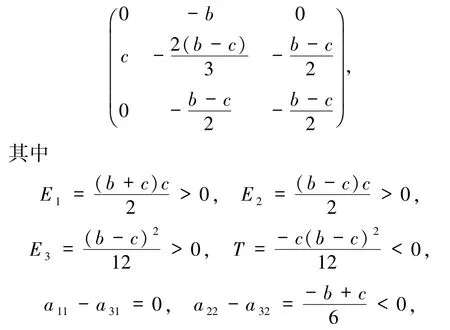
满足引理3 中条件1）.因此三循环优势系统1 做负变换后是全局稳定的，原系统1 除正平衡点外异宿环全局吸引的.由此可知：当时，三循环优势系统2、8、9、10、11 存在中心，三循环优势系统6、7 具有全局稳定性，三循环优势系统1、3除正平衡点外异宿环全局吸引.同理，结合引理1 ～3，得到定理.

定理1在具有行为误差的交替捐赠博弈中，当成本收益比k∈（0，1）不同取值时，可以对具有正平衡点的三循环优势系统关于动力学行为进行完全分类，见表2 所示.对应相图如图1 所示，其中空心表示不稳定驻点，实心表示稳定驻点.

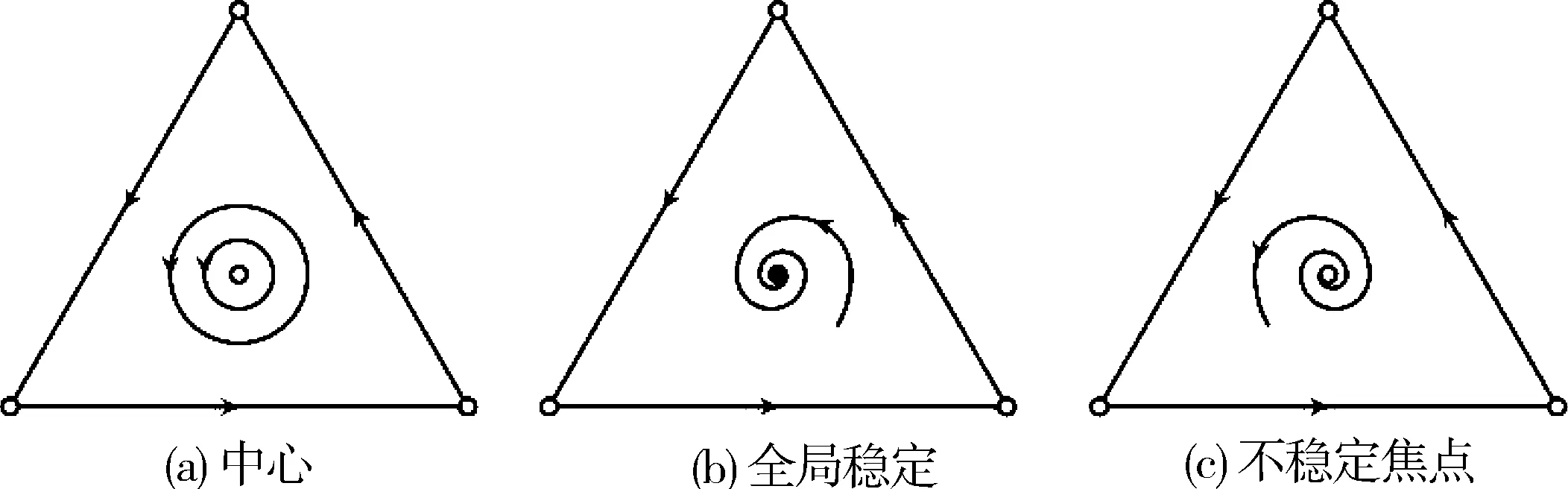
图1 三循环优势系统动力学行为相图Fig. 1 Phase diagram of dynamic behavior of three-cycle superior system

表2 具有行为误差的交替捐赠博弈中不同成本收益比三循环优势系统的完全分类Tab. 2 A complete classification of three-cycle advantage systems with different cost-benefit ratios in an alternating donation game with behavioral errors

3 四循环系统永久生存性

经运算得到了不同成本-收益比下交替捐赠博弈中四循环优势系统的数量，下面将进一步讨论存在正平衡点的四循环优势系统的永久生存性.具有正平衡点的四循环优势系统如表3 所示.

表3 存在正平衡点的四循环优势系统Tab. 3 Four-cycle advantage systems with positive equilibriums

定义1［17］对于Sn上的复制方程

（4）式的永久生存性即存在 δ ＞0 使得对所有 i，只要 xi（0）＞0，就有

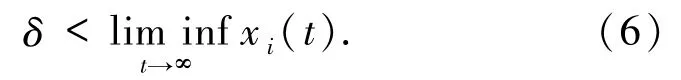
对于（5）式永久生存性还需存在D，使得

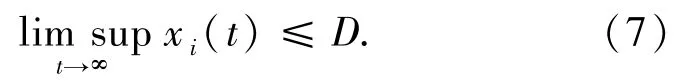
引理 4［17］复制系统（1）为永久生存的，如果存在向量P∈int Sn使得

对所有驻点x∈bd Sn成立.

定理2具有收益矩阵

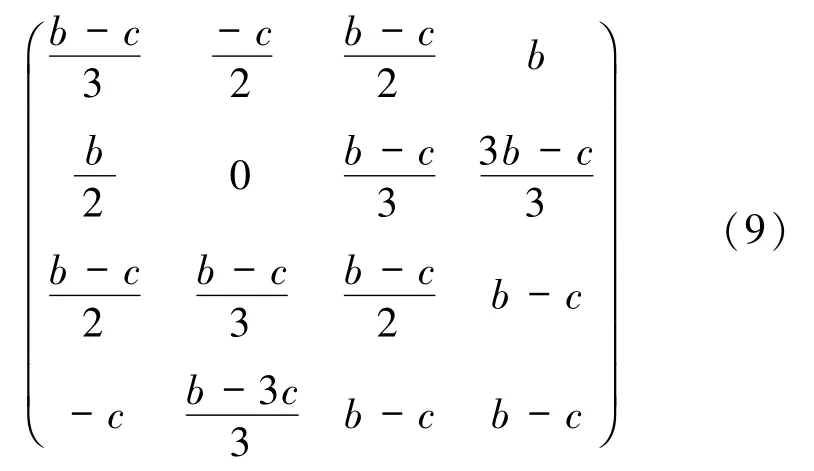
将边界驻点分别带入（8）式有：

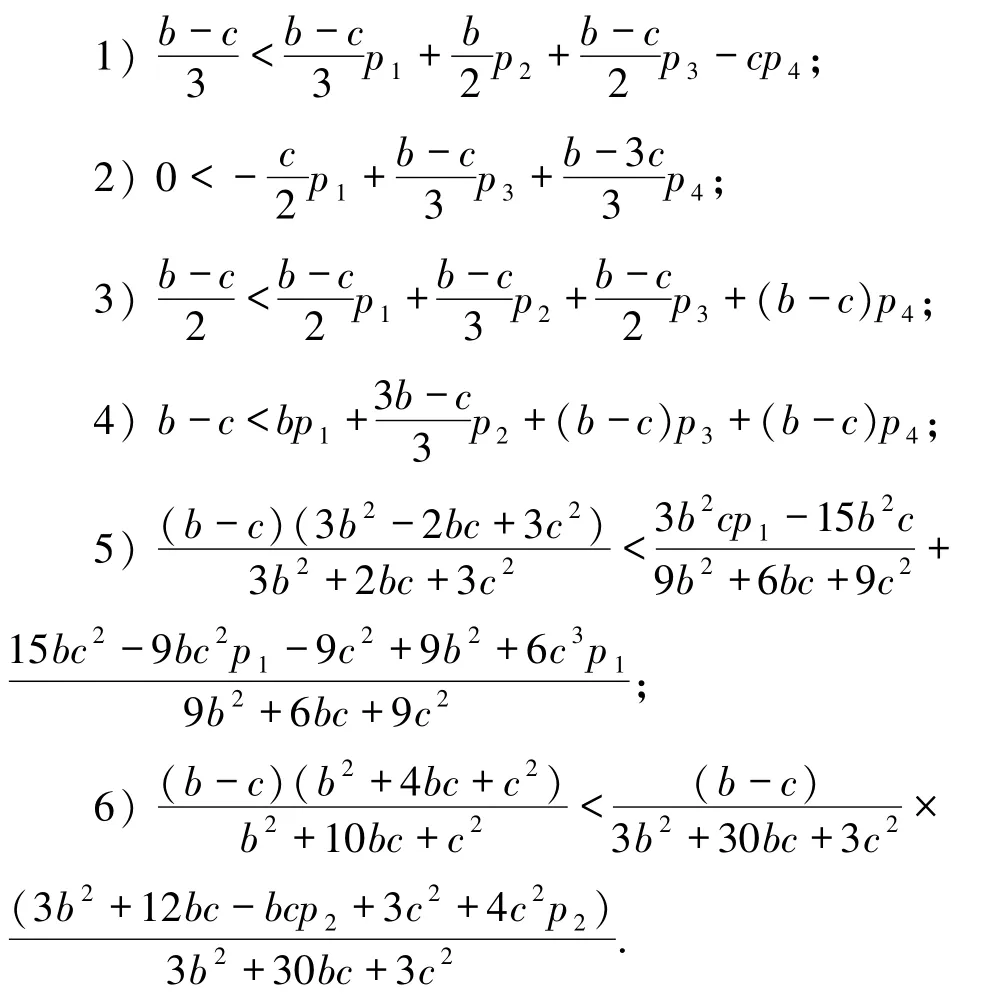
又由 p1，p2，p3，p4＞0，且 p1+p2+p3+p4＝1，不等式可简化为等价形式：

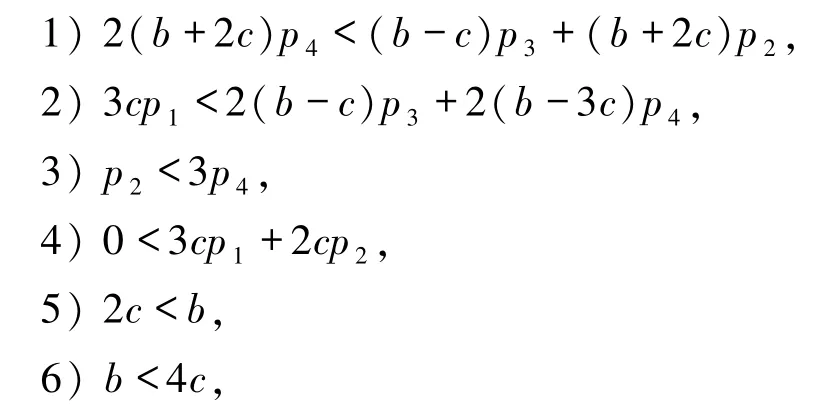
其中，不等式4）～6）恒成立.因此验证系统的永久生存性只需适当的取向量P使其满足不等式1）～3）即可.令则满足P的所有限制条件，故存在向量P 使得（8）式成立，得证.

系统［S0，S7，S14，S10］具有收益矩阵：

将其边界驻点带入（8）式有：

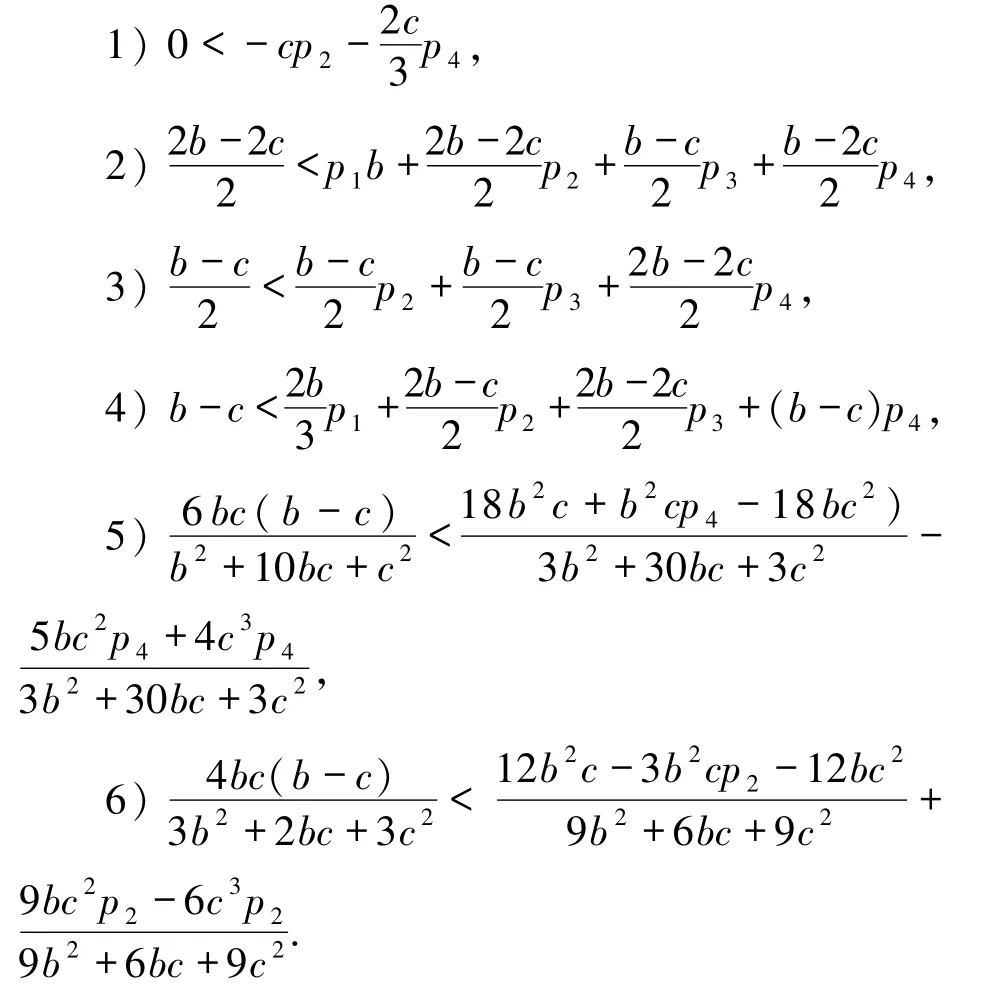
又P∈int Sn，即P是非负的，与1）矛盾.由此，该系统不满足永久生存性的充分条件.同理，可验证存在正平衡点的四循环优势系统的永久生存性，从而定理2 得证.

4 极限环的存在性

在第二节中是以交替捐赠博弈为背景展开讨论的，接下来在更一般的交替囚徒困境中讨论极限环的存在性和稳定性.

在双人博弈中若收益关系满足：S ＜0，S ＜ P ＜R ＜T 和 T+S ＜2R，则称为囚徒困境.

考虑具有收益矩阵

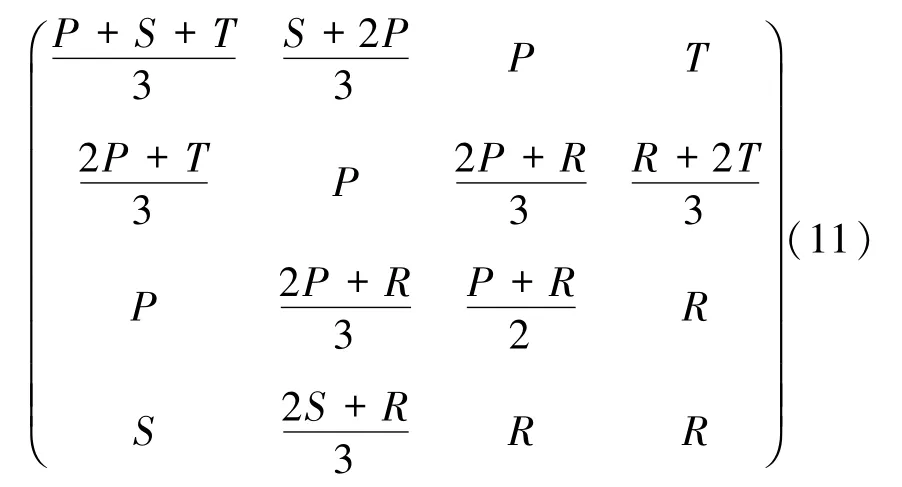
的复制系统，由 n 维复制系统与 n -1 维Lotka -Volterra系统的等价性，具有收益矩阵（11）的复制系统相对应的Lotka-Volterra系统为：

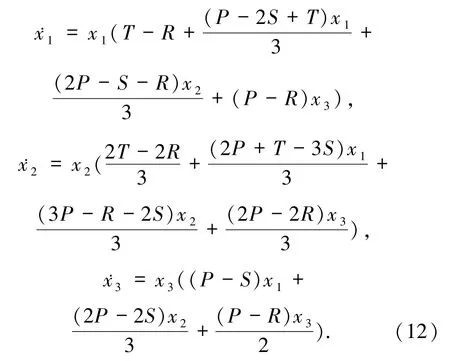
假设正平衡点存在，则

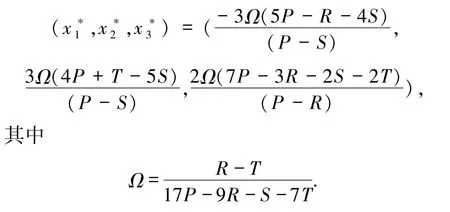
下面给出本文的主要结果.

定理3具有收益矩阵（11）的四循环系统（1）如果有正平衡点，则当参数适当选取时，至少存在一个不稳定的极限环.

又根据高（n）维系统构造极限环的一般降维原理，系统线性部分在正平衡点处的特征值具有非正实部，且需 n -2 个负实部.对此问题可由（14）式保证：

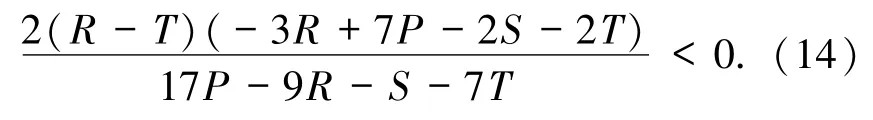
又（13）和（14）式等价于

在（15）式条件下，令

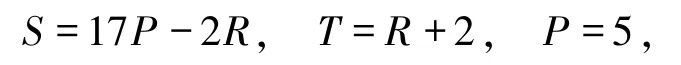
则系统的收益矩阵变换为

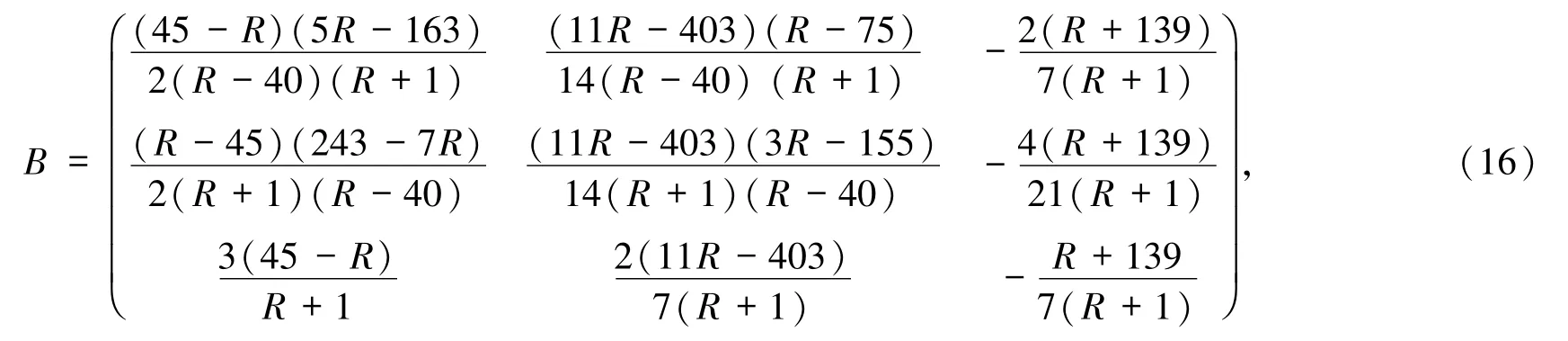
（16）式具有一个负特征值和一对共轭纯虚根特征值［18］当且仅当

即

对系数矩阵（16）做变换 y ＝ Tx，

fij、gij是关于R 的高次多项式，则变换后系统线性部分具有以下形式

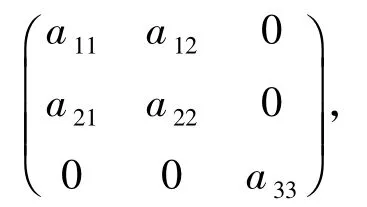
其中aij是关于R 的高次多项式.变换后的线性系统有一对共轭纯虚特征值和一个负实特征值，现计算局部中心流形 y3＝ h（y1，y2）.

将 y3＝ h（y1，y2）展开为

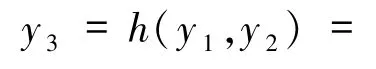
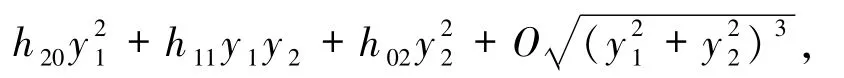
并代入不变流形［3］所满足的方程求得一阶焦点量

其中，f1、f2、g1、g2、g3、g4分别是 6、90、31、8、20、9项的多项式.

为得到小扰动极限环，需在满足（17）式的条件下判断一阶焦点量的正负性.又（17）式精确到10-100的 3 个区间形式解分别为［a1，b1］、［a2，b2］、［a3，b3］，其中分数a2、a3的分子分母分别是长度为103、101 位的整数，分数b2、b3的分子分母是长度为103 和102 位的整数.又（17）式与L1的分子分母的结式都不为零，因而与L1的分子分母都无公根.即在条件（17）下L1分子分母的所有因子都不为零，故判断L1的正负性只需通过判断非平方因子f1、f2、g1的正负性即可.

利用实根分离算法［18］的极大极小多项式方法有

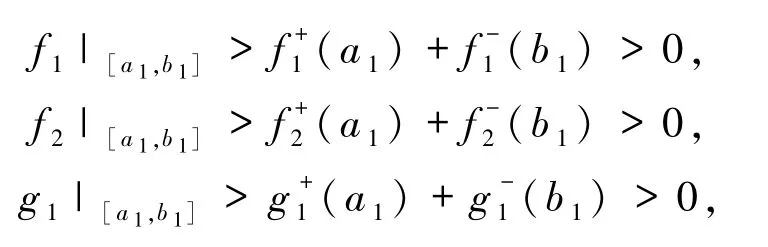
即当 R 在区间［a1，b1］上时，L1＜0.同理可得：

f1｜［a2，b2］＞ 0， f2｜［a2，b2］＜ 0， g1｜［a2，b2］＞ 0，f1｜［a3，b3］＞ 0， f2｜［a3，b3］＜ 0， g1｜［a3，b3］＞ 0.因此，当 R∈［a2，b2］或 R∈［a3，b3］时，L1＞ 0.由Hopf分支［19］可判定 Lotka-Volterra 系统（12）存在不稳定极限环，再由具有收益矩阵（11）的复制系统与Lotka-Volterra系统（12）的同胚性定理3 成立.