基于GHZ 型纠缠态的双向受控隐形传态及安全性

唐 茜， 柏明强， 莫智文

（四川师范大学数学科学学院，四川成都610066）

量子纠缠作为一种重要的物理资源，在量子通信方面有广泛的应用，如量子隐形传态、量子密集编码、量子密钥分配等，其中，量子隐形传态是量子通信中引人瞩目的课题之一.量子隐形传态是间接的量子态传输方式，通过量子纠缠建立量子信道辅以经典信道，可以实现未知量子态的远程传输.1993 年，Bennett 等［1］首次提出量子隐形传态的概念，利用量子纠缠态的非局域性，首先在通信双方之间分发EPR 对来作为量子信道，然后通过量子测量及相关的幺正变换实现量子态的远程传输.而受控隐形传态则是在1998 年由Karlsson 等［2］首次提出，是以GHZ纠缠态作为量子信道，在控制方的帮助下重建未知的单量子态.

随着量子研究的发展，隐形传态由单向隐形传态发展到双向隐形传态［3-9］，受控隐形传态发展到双向受控隐形传态［10-29］等形式.如吴柳雯等［3］提出了以四粒子Ω 纠缠态作为量子信道实现单量子比特、双量子比特以及受限三量子比特的双向隐形传态；刘乾等［6］利用合适的三粒子GHZ 纠缠态构造量子信道，实现EPR 对双向隐形传态；孙新梅等［10］提出基于六粒子最大纠缠态的双向受控隐形传态方案；王小宇等［22］提出一种利用非最大纠缠态作为量子信道，实现任意Bell型纠缠态的双向受控概率隐形传态；王贵祥等［27］提出基于三粒子GHZ态实现未知单粒子态的三方或四方参与的双向受控隐形传态.

尽管到目前为止提出了众多的双向受控隐形传态方案，但是这些方案传输粒子至多是二粒子态，且未对量子信道的安全性进行讨论分析.本文针对多粒子量子态的双向受控隐形传态这一问题，提出利用两对合适的M +1（＞N +1）粒子的GHZ型纠缠态为量子信道，实现N（＞2）粒子的GHZ型纠缠态的双向受控隐形传态方案，且讨论分析方案的效率和安全性，说明了方案是高效安全的.同时，本文选取的量子信道GHZ 型纠缠态在实验中容易制备，相应的测量操作也方便简单，易于实现双向受控隐形传态.

1 N粒子GHZ 型纠缠态的双向隐形传态方案

假设Alice拥有如下N粒子GHZ型纠缠态

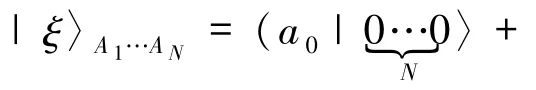
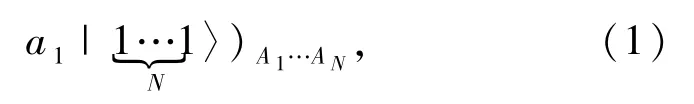
其中非零实数 a0、a1满足｜a0｜2+ ｜a1｜2＝ 1.Bob 拥有如下N粒子GHZ型纠缠态

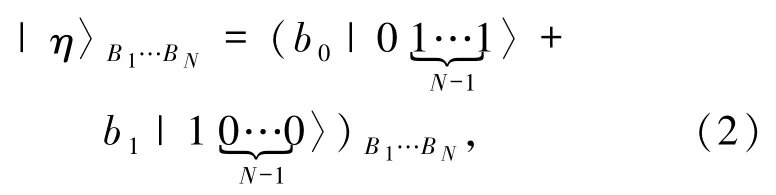
其中非零实数 b0、b1满足｜b0｜2+ ｜b1｜2＝1.

现在 Alice 想要将态 ｜ξ〉A1…AN传给 Bob，同时Bob 想要将态｜η〉B1…BN传给 Alice.为了完成这个双向传输任务，Alice、Bob 与控制者 Charlie 共享如下一对合适的M +1 粒子的GHZ 型纠缠态作为量子信道：

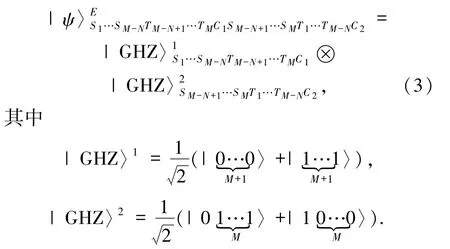
粒子 S1，S2，…，SM属于 Alice，粒子 T1，T2，…，TM属于 Bob，粒子 C1、C2属于 Charlie.

整个方案的流程图如图1 所示.

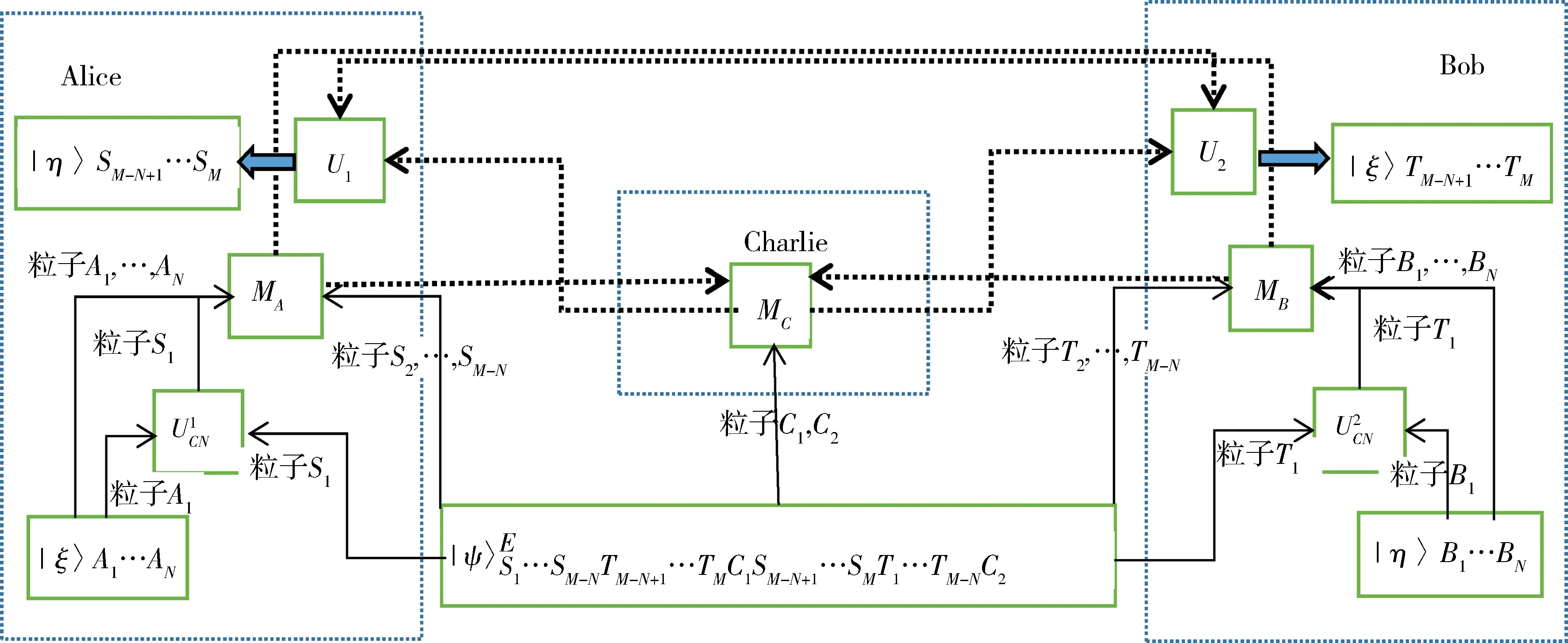
图1 方案流程图Fig. 1 Scheme flow chart

在本方案中，整个系统的初态为

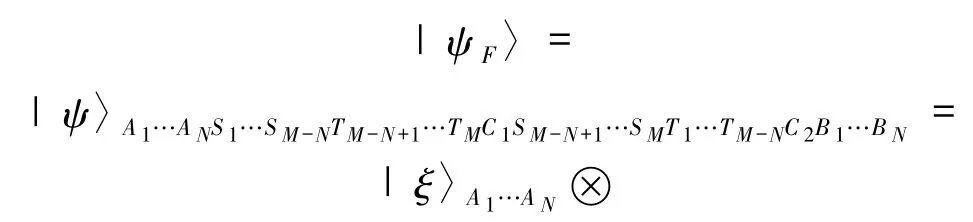
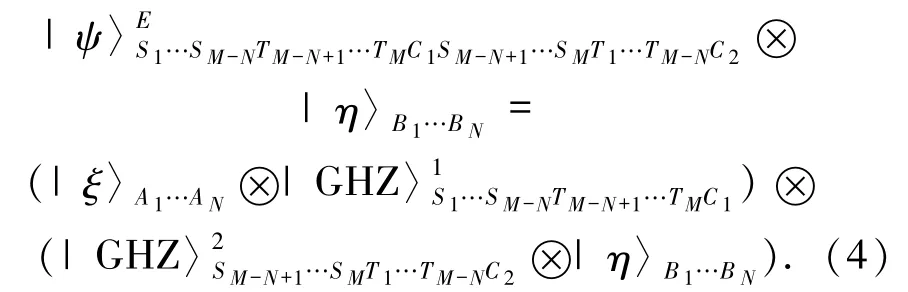
方案按以下4 个步骤依次进行.

第一步：Alice和Bob分别以量子比特A1和B1为控制相位，量子比特S1和T1为目标相位，进行受控非门操作，得到的结果为

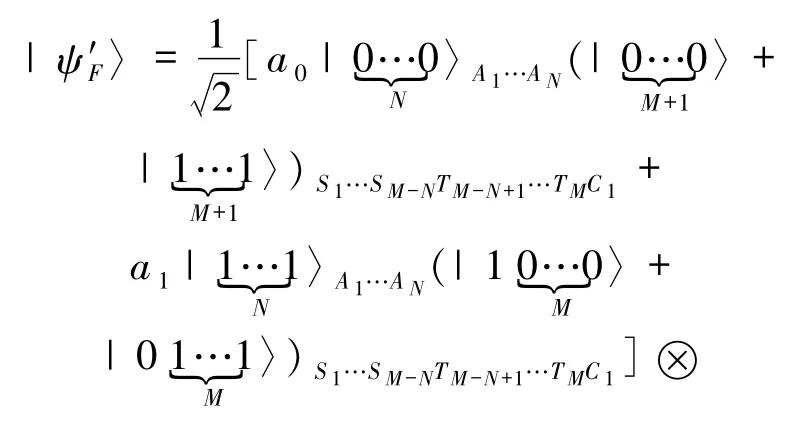
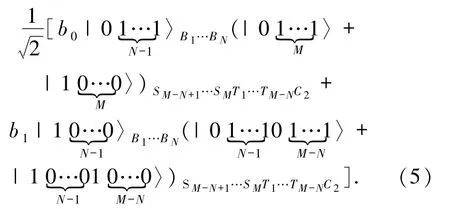
第二步：1）Alice 和 Bob 分别对粒子 S1、T1进行 Z ＝｛｜0〉，｜1〉｝基测量，并通过经典信道公布测量结果.其可能的测量结果有4 种，概率均为1/4.令 Alice 的粒子 A1，A2，…，AN，S2，S3，…，SM-N分别为 1，2，…，N，N +1，…，M -1，Bob 的粒子 B1，B2，…，BN，T2，T3，…，TM-N分别为 1′，2′，…，N′，（N +1）′，…，（M-1）′，经过测量后的系统坍塌为：

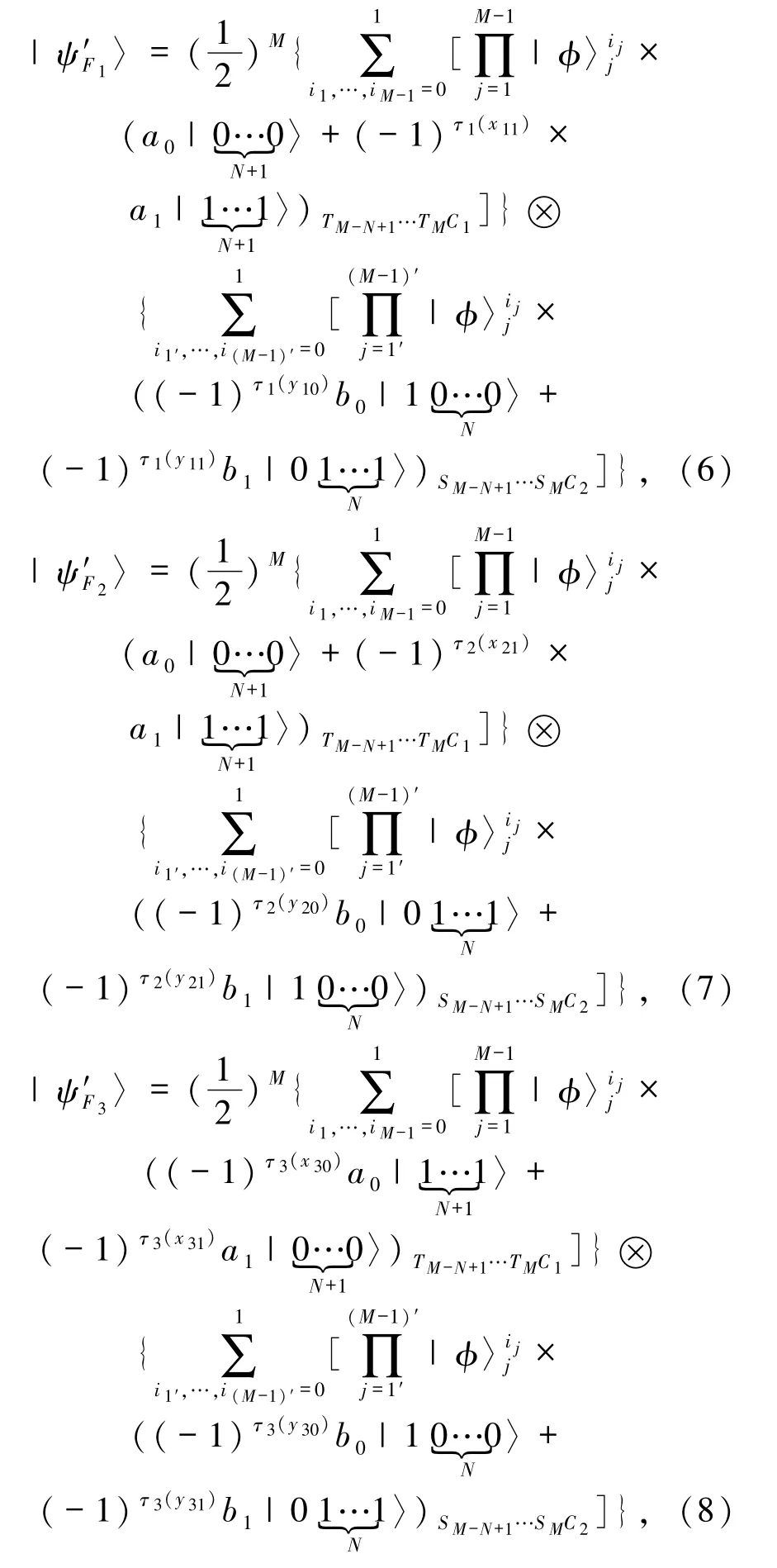
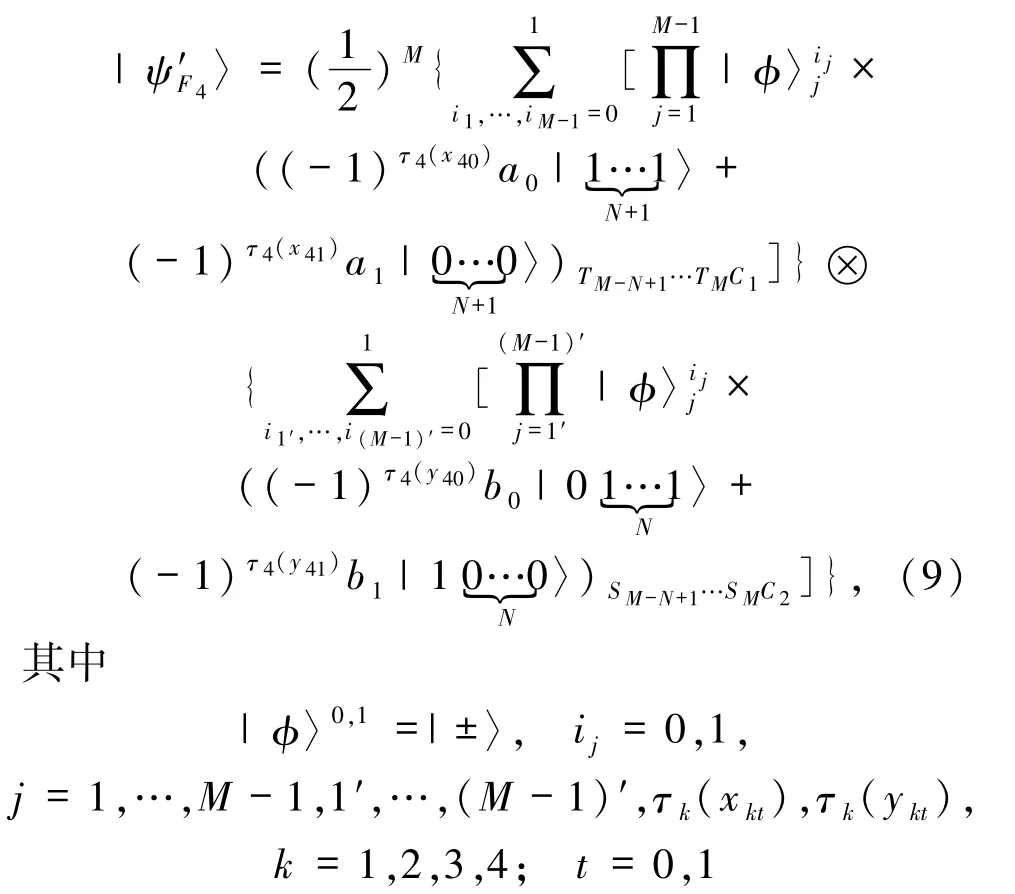
表 1 xkt、ykt（k=1，2，3，4；t=0，1）的表示情况Tab. 1 Represents the situation of xkt，ykt（k=1，2，3，4；t=0，1）

2）Alice和Bob分别对自己的粒子1，2，…，N，N+1，…，M-1 和 1′，2′，…，N′，（N+1）′，…，（M-1）′进行 X ＝｛｜+〉，｜-〉｝基测量，并向对方及控制者Charlie公布测量结果.

第三步：若控制者Charlie 同意双方通信，则控制者 Charlie对自己的粒子 C1、C2进行 X ＝｛｜+〉，｜-〉｝基测量，并将测量结果通过经典信道公布给通信双方.

第四步：经过测量，系统坍塌为相应的态

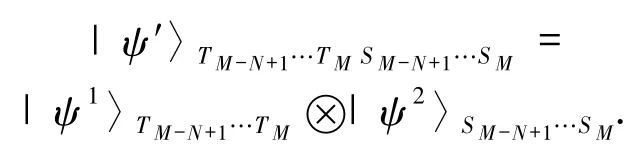
通信双方根据对方公布测量结果相对应的τk（xkt）、τk（ykt）（k ＝1，2，3，4；t ＝0，1）的奇偶情况及控制方的测量结果采用表2 相对应的幺正变换，即可得到对方待传的态.

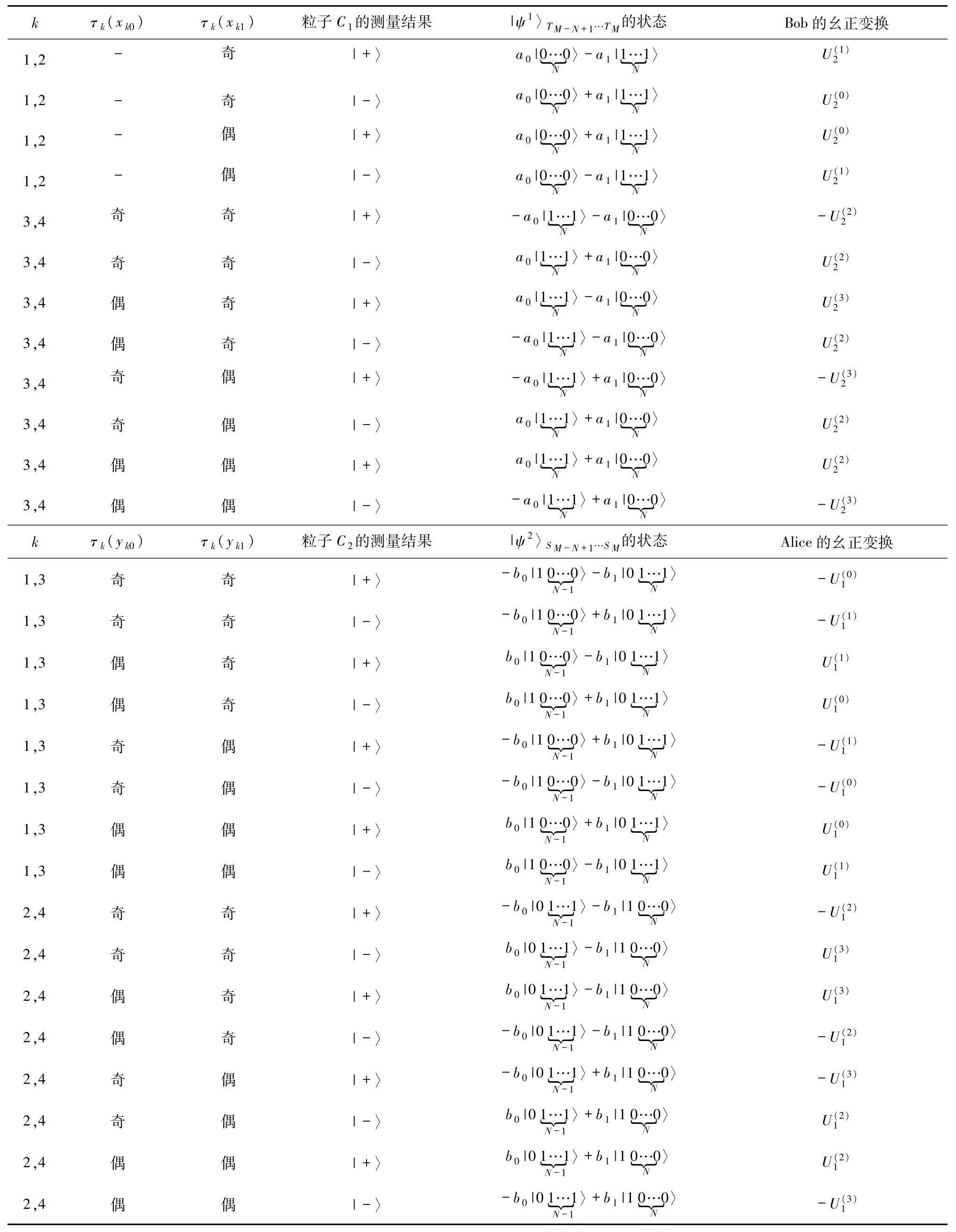
表 2 τk（xkt）τk（ykt）的奇偶性，Charlie 的测量结果，相应的坍塌态及幺正变换Tab. 2 The parity of τk（xkt）τk（ykt），measurement results of Charlie，corresponding collapse state and unitary transformation

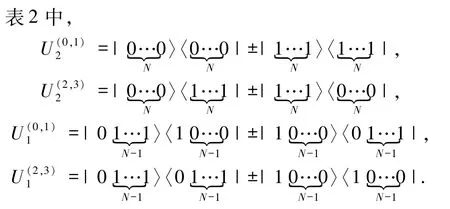
举例说明：如果 Alice 的测量结果为｜0〉S1｜+〉1…｜+〉M-1，Bob的测量结果为｜0〉T1｜ + 〉1′…｜+ 〉（M-1）′，控制者 Charlie 的测量结果为 ｜+ 〉C1｜+〉C2，则 k ＝1，τk（xk1）、τk（yk0）、τk（yk1）中取值为1 的有0（偶数）个，且其余粒子坍塌为

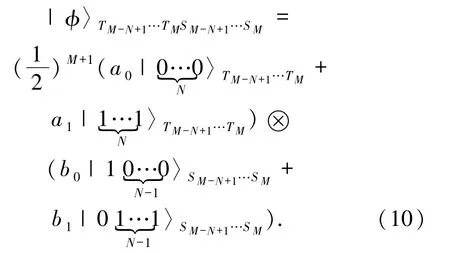
因此，通信双方Alice 和Bob 只要对自己所拥有的量子比特作如表2 中相应的幺正变换：

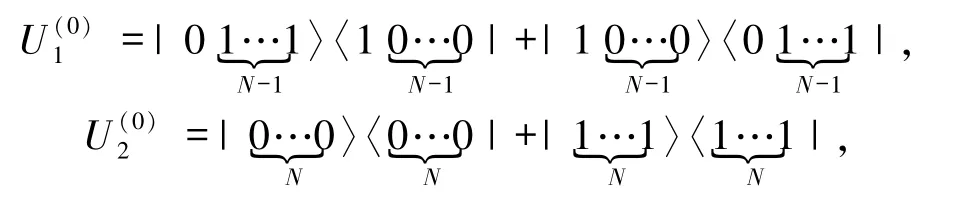
便可重构N粒子GHZ 型纠缠态，实现双向受控隐形传态.

2 效率分析

效率是设计方案所必需考虑的重要因素.在量子通信的协议中，常用2 种效率公式来评估方案：

1）量子密码协议的效率［30］

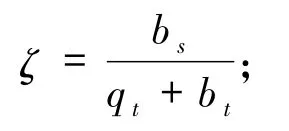
2）量子比特效率

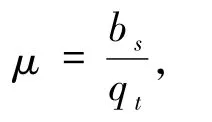
其中bs、qt和bt分别表示为通信方得到的秘密量子比特数、总量子比特数（秘密量子比特数与量子信道比特数之和）和经典比特数.本文的2 个效率分别为

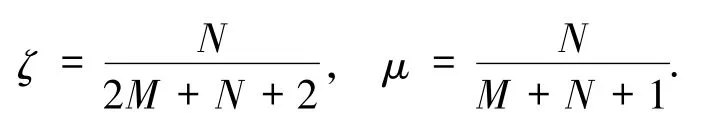
要使本文效率达到最高，则传输N 粒子GHZ 型纠缠态需选择M +1 ＝N +2 粒子GHZ型纠缠态来构建信道，2 个效率变为

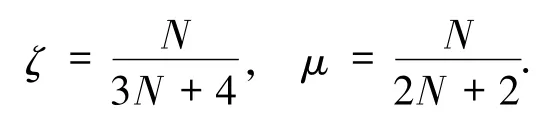
由于本方案是双向传输N（＞2）粒子GHZ 型纠缠态的隐形传态，且本方案在理想情况下效率与传输的粒子数成正比，而已有的一些方案双向传输的是单粒子或二粒子态.若本文以一对五粒子GHZ 型纠缠态为量子信道双向传输三粒子GHZ 纠缠态为例，与已有的一些方案相比，方案效率比较如表3.

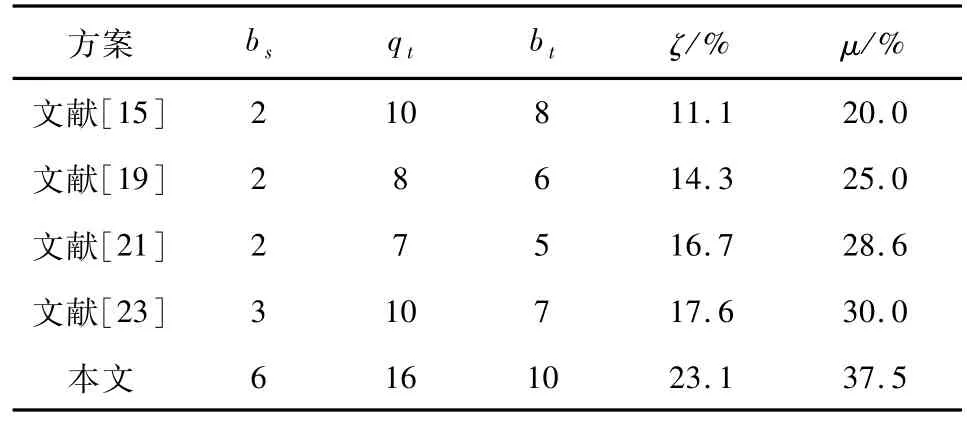
表3 方案效率比较Tab. 3 Scheme efficiency comparison

从表3 可以看出文献［15，19，21］双向传输的是单粒子态，文献［23］双向传输的是不对称态（单粒子态与二粒子态），且这些文献的效率均低于本文效率.由于这些文献秘密量子比特数bs与本方案的取值不同，接下来考虑这些文献的秘密量子比特数bs均为6（通信双方共传输6 个粒子）可能得到的效率，情况如下（以文献［15］为例，其他文献情况类似）：

文献［15］的量子信道是8 粒子态，其中控制方Charlie拥有2 个粒子，在控制方同意通信的情况下，通信双方利用6 个粒子传输2 个粒子.由于控制方的粒子数与传输的粒子数无关，则在控制方粒子数不变的情况下，通信双方传输6 个粒子理论上需要18 个粒子，因此量子信道变为20 粒子态，总量子比特数qt变为26，经典比特数bt变为20，效率ζ ＝13%，μ ＝23.1%.其他文献情况类似，则在文献［19］中有：

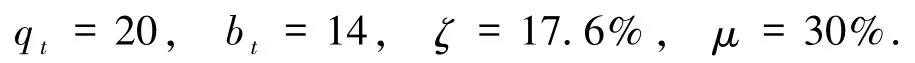
在文献［21］中有：

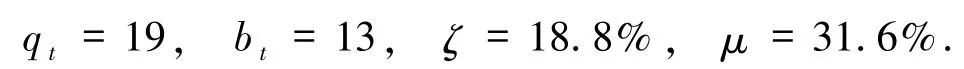
在文献［23］中有：

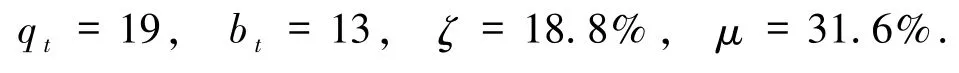
在秘密量子比特数bs均为6 的情况下，通过对比，本文的效率更高.

3 安全性分析

一个安全的受控隐形传态协议应满足如下几点：

1）在通信结束前，通信双方无法得到对方的待传态；

2）窃听者无法通过通信双方的交互信息来获取待传态；

3）能抵抗截获-重发攻击，纠缠攻击等；

4）控制者是可信的，即控制者只诚实的执行协议操作.

本文以一对五粒子GHZ型纠缠态构成的量子信道双向传输三粒子GHZ 纠缠态为例进行安全性分析（其他情况类似）.设待传三粒子 GHZ 纠缠态为：

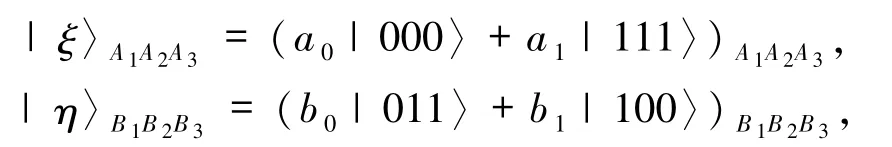
且非零实数 a0、a1、b0、b1满足

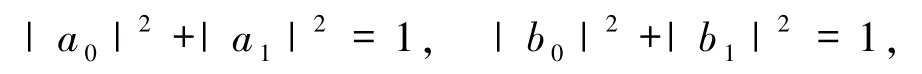
则量子信道、系统初态分别如下：

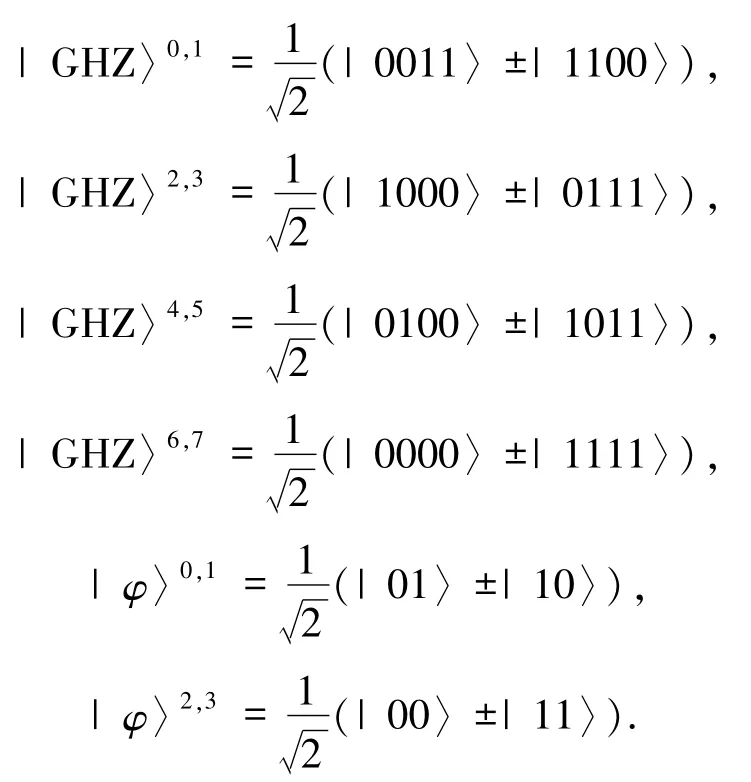
3.1 外部攻击基于量子力学的基本原理，如测不准原理和量子不可克隆原理，量子的通信相对于经典通信是安全可靠的.一般情况下，窃听者Eve有两种常见的攻击策略.一种是截获-重发攻击，即窃听者Eve截取控制方Charlie分发给发送者Alice或Bob所发送的量子态，测出一个结果，然后根据自己测量的结果产生一个新的量子态发送给接收者Bob或Alice.这种简单的攻击在量子密钥分配协议中已经被完美地证明该攻击无效，即窃听者Eve不能从量子密钥分配的过程中得到任何有效的信息.另一种是纠缠攻击，本文的纠缠攻击有以下2 种情况：

1）信道共享阶段的纠缠攻击.若Eve 的纠缠攻击发生在信道共享阶段，即对量子信道发起纠缠攻击.假设窃听者Eve想办法将自己的初态纠缠在量子信道中的 Bob 粒子 T1、T2、T3、T4上（相同地可以纠缠在 Alice的粒子上），即以 T1、T2、T3、T4为控制相位，E′1、E1、E2、E3为目标相位进行受控非门操作，则量子信道处于14 粒子纠缠态，即

由（13）式可以看出：窃听者Eve与接受者Bob的地位相同，但这种情况不可能出现.因为当Alice 和Bob随机选择一些相应的粒子对进行相应的｜GHZ〉基测量和 Charlie 对粒子进行 Bell 基测量后，通过分析三人的测量结果且对比（11）和（13）式，可以发现有50%的测量结果不相关联，如Alice的测量结果是 ｜GHZ〉0，Charlie 的测量结果是｜φ〉0，由（11）式可以知道相关联 Bob 的测量结果为｜GHZ〉2，而由（13）式发现 Bob 的测量结果有 2种情况，通过分析比较有50%的测量结果不相关联.从而得到通信信道是不安全的结论，则通信双方及控制者会舍掉该信道且重选新信道，因此，该阶段的纠缠攻击是无效的.

2）通信阶段的纠缠攻击.若Eve 的纠缠攻击发生在通信阶段，即对系统初态｜ψF〉发起纠缠攻击.假设 Eve 将初态为｜0〉E1、｜0〉E2、｜0〉E3、｜0〉E4、分别纠缠在系统初态｜ψF〉中的 Alice、Bob 的粒子 S1、S2、S3、S4、T1、T2、T3、T4上，即以 S1、S2、S3、S4、T1、T2、T3、T4为控制相位为目标相位进行受控非门操作，则系统初态变为

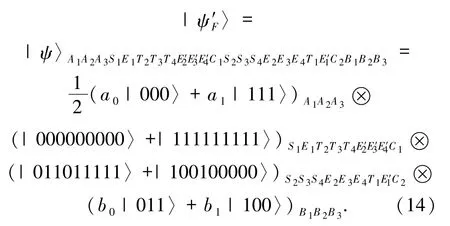
首先以量子比特A1和B1为控制相位，量子比特S1和T1为目标相位，进行受控非门操作，得到的结果为

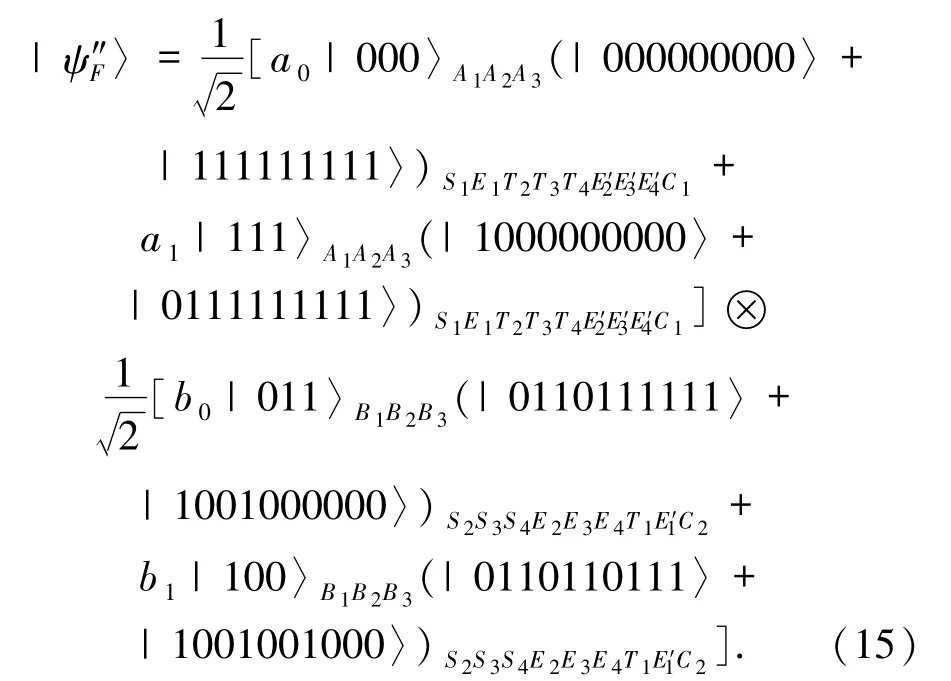
然后 Charlie 对粒子 C1、C2进行 X 基测量，Alice、Bob分别对粒子S1、T1进行Z 基测量，以及对粒子A1、A2、A3、B1、B2、B3进行 X 基测量，同时窃听者Eve 需对粒子 E1、E′1进行 Z 基测量，且与粒子 S1、T1的测量结果相同.如Alice 的测量结果为｜0〉S1｜+〉A1｜+〉A2｜+ 〉A3，Bob 的测量结果为 ｜0〉T1｜+〉B1｜+〉B2｜+ 〉B3，控制者 Charlie 的测量结果为 ｜ + 〉C1｜ + 〉C2，则 Eve 的测量结果为 ｜0〉E1｜0〉E1′，且系统坍塌为（其他测量结果情况类似）

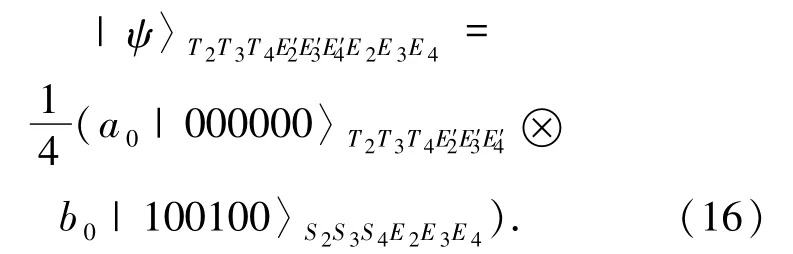
由（20）式可以看出，窃听者Eve得不到完整的待传态，即纠缠攻击是无效的结论.

3.2 内部攻击不诚实的参与者比窃听者Eve 更容易窃取信息，因为不诚实的参与者合法地知道部分信息.不妨假设Bob 不可信（称为Bob*），他想获得Alice的待传态，而不被Alice 和Charlie 发现.由于Bob*不知道Alice和Charlie的操作和测量结果，则Bob*直接对系统初态｜ψF〉中Alice和Char-lie的粒子 A1、A2、A3、S1和 C1进行测量.假设Bob*首先对粒子S1进行单粒子测量，测量基可能为

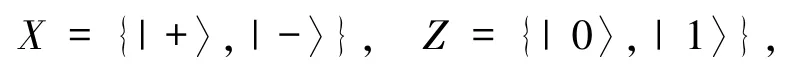
则其可能的测量的结果有4 种，经测量后系统初态坍塌为：

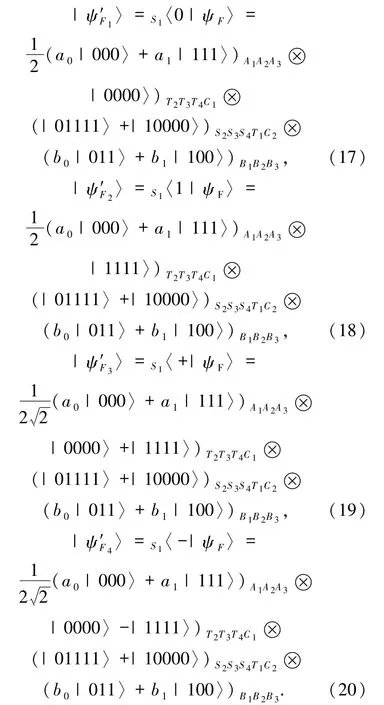
由（17）～（20）式可以看出，当Bob*对粒子 S1进行Z 基测量时，Bob*再对其他粒子进行任何投影测量都得不到完整的待传态，则Bob*应对粒子S1进行X基测量.假设S1的测量结果为｜+〉，则系统坍塌态为接下来 Bob*对中粒子 A1、A2、A3及C1进行单粒子测量，则测量结果可能有256 种.如测量结果为 ｜+〉A1、｜+〉A2、｜+〉A3、｜+〉C1，则系统坍塌为（其他测量结果情况类似）

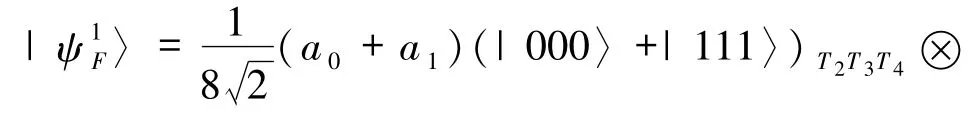
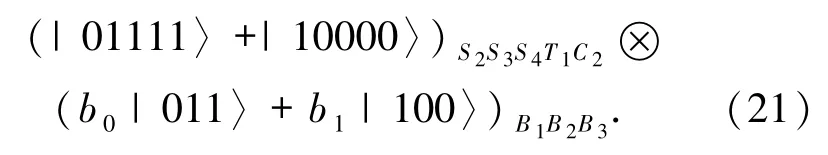
由（21）式可以看出，不可信的参与者Bob*得不到Alice的待传态，即内部攻击是无效的结论.

3.3 安全性对比本文与已有的文献［13，15 -16，19，21］相比更安全.例如文献［21］（其他文献类似）中Alice和Bob待传输的量子态分别为：

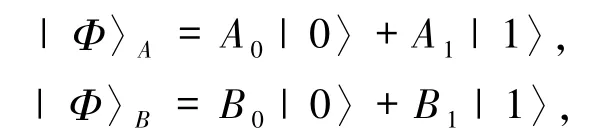
其中复数 A0、A1、B0、B1满足

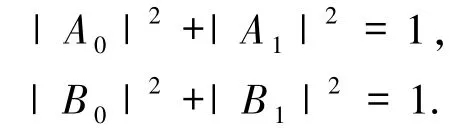
Alice、Bob和控制者Cindy 共享一五粒子Cluster 态为量子信道，则信道表示为

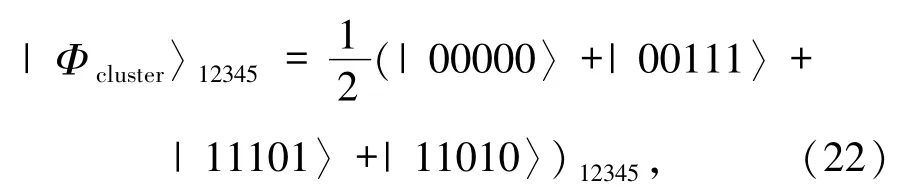
整个系统初态为

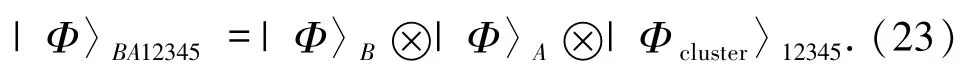
其中粒子 A、1、5 属于 Alice，粒子 B、2、3 属于 Bob，粒子4 属于控制者Cindy.

若方案的攻击为内部攻击，假设参与者Bob 是不可信的（称为Bob*），则Bob*不知道Alice 和Charlie的操作和测量结果. Bob*直接对系统初态｜Φ〉BA12345中 Alice 和 Charlie 的粒子 A、1、5 和 4 进行测量，假设Bob*对粒子A，1 进行Bell基测量和对粒子4 进行单粒子测量，单粒子测量基可能为

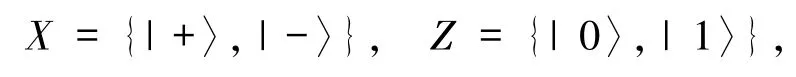
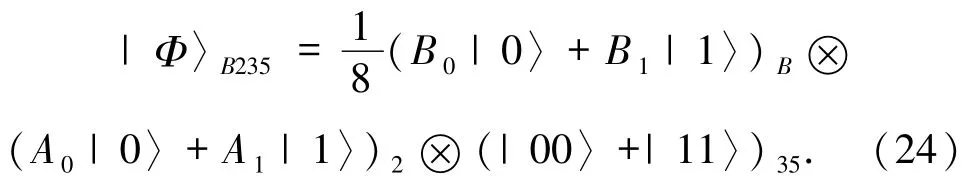
由（24）式可知，Bob*有可能在不被Alice 和Charlie发现情况下得到Alice待传输的信息A0｜0〉+A1｜1〉，即在内部攻击下文献［21］是不安全的.

综上所述，与文献［21］相比，本文的隐形传态方案具有更高的安全性.

4 结束语

本文提出了基于M +1 粒子GHZ 型纠缠态实现N粒子GHZ 型纠缠态双向受控隐形传态方案.在此方案中，通信双方Alice和Bob及控制方Charlie事先共享一对合适的 M +1 粒子GHZ 型纠缠态，利用GHZ 型纠缠态的关联性及顽固性强的优点实现双向受控隐形传态.通信开始后，Alice 和Bob首先分别对个别粒子进行受控非门操作，再对该粒子进行Z基测量及对其他部分粒子进行X 基测量，并通过经典信道向对方及控制方Charlie 公布测量结果.然后 Charlie 对粒子 C1、C2进行 X 基测量，并将测量结果通过经典信道公布给通信双方.最后通信双方根据所有公布的测量结果对各自粒子做相应的幺正变换，即可实现双向受控隐形传态.同时对方案进行效率及安全性分析，证明本文方案具有更高的效率及安全性.