由一道抛物线最值问题引起的探究与思考

安徽 洪汪宝

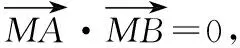
本题是笔者所在学校2020届高三第一次模拟考试的第16题，处于填空题压轴的位置，是一道典型的最值问题.主要考查直线与抛物线的位置关系、平面向量的数量积、点到直线的距离公式等多个知识点，考查数形结合思想、函数与方程思想、化归与转化思想等多种数学思想方法.要求学生具备扎实的运算求解能力以及分析问题和解决问题的能力.

本题满分5分，但笔者所在班级(理科班)的均分只有1.56分，难度系数为0.312，与预期有差距.因为本题题干简洁，题意清楚，目标明确，起点比较低，大部分学生都可以动笔计算，但深入较难，对学生的能力要求逐渐提升，在试题分析过程中，不少学生也反映没有发现直线AB过定点导致计算进行不下去.下面给出本题的求解过程，对其解法进行探究，并在此基础上将问题一般化，进行拓展探究，发现圆锥曲线中一系列的结论.

1.解法探究

1.1先证直线AB过定点

读完题，弄清题意，联想到一道课本中的习题：

由人民教育出版社出版的A版高中数学教科书选修2-1第73页习题2.4A组第6题(图略)：直线y=x-2与抛物线y2=2x相交于A,B两点，求证：OA⊥OB.

本题的逆命题可表达为：不过原点O的直线l与抛物线y2=2x相交于A,B两点，若OA⊥OB，则直线l过定点(2,0).经过验证该命题也是真命题，在此基础上，还可以得到一般的结论：

结论1：直线l与抛物线C:y2=2px(p>0)交于异于原点O的两点A,B，OA⊥OB⟺直线l过定点(2p,0).

如果知道上述结论，我们必然想到本题中的直线AB是否过定点呢？下面完成其推导过程.

根据条件可设AB:x=my+n，A(x1,y1),B(x2,y2)，

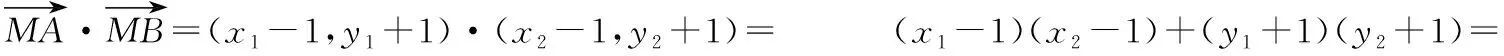
(y1+1)(y2+1)[(y1-1)(y2-1)+1]=0，

因为(y1+1)(y2+1)≠0，则(y1-1)(y2-1)+1=0，

展开整理得y1y2-(y1+y2)+2=0.(*)

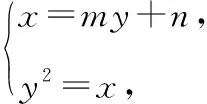
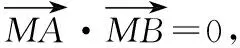
1.2求点到直线距离的最大值

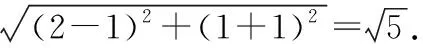
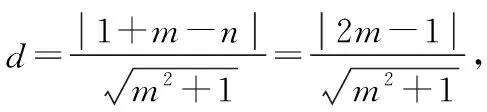
两边平方，并整理得到关于m的方程(d2-4)m2+4m+d2-1=0，方程有实根.

当d>0且d≠2时，其判别式Δ=16-4(d2-4)(d2-1)≥0，

解法3：同解法2

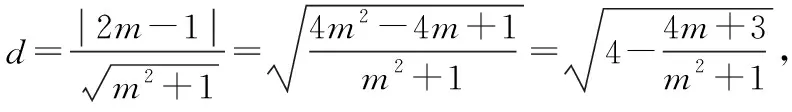
点评：解决平面解析几何的最值问题通常有两种策略：一种利用几何性质，另一种利用代数方法.解法1直接利用几何性质，简单快捷；解法2、解法3与解法4都是先利用点到直线的距离公式求出距离的函数表达式，在此基础上转化为求函数的最值问题.解法2利用了判别式，解法3利用了均值不等式，解法4利用了柯西不等式.相比较而言，本题利用几何性质求最值效果更好.

2.结论探究

由上面的求解过程，特别是求证直线过定点的过程，将问题一般化，于是得到下面的结论：

结论2：已知抛物线C:y2=2px(p>0)上一点M(x0,y0)，直线l与抛物线C交于异于点M的两点A,B，若MA⊥MB，则直线l过定点(x0+2p,-y0).

证明：设AB:x=my+n，A(x1,y1),B(x2,y2)，

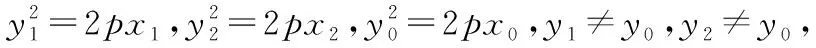
=(x1-x0)(x2-x0)+(y1-y0)(y2-y0)

因为(y1-y0)(y2-y0)≠0，则(y1+y0)(y2+y0)+4p2=0，

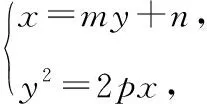
根据韦达定理得y1+y2=2pm,y1y2=-2pn，代入(1)，得my0-n+x0+2p=0，

所以直线AB过定点P(x0+2p,-y0).

那么其逆命题成立吗？很容易得到以下结论：

结论3：已知抛物线C:y2=2px(p>0)上一点M(x0,y0)，过定点(x0+2p,-y0)的直线l与抛物线C交于异于点M的两点A,B，则MA⊥MB.

抛物线有这种性质，那么椭圆呢？先从特殊情况出发，得到：

将点M的位置一般化，于是得到：

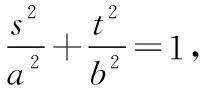
不妨设直线l:y=kx+m，A(x1,y1),B(x2,y2)，

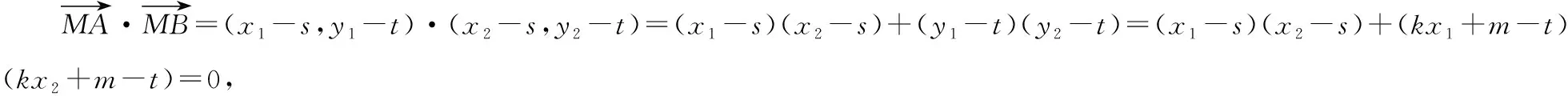
展开整理得(k2+1)x1x2+(km-kt-s)(x1+x2)+m2+s2+t2-2mt=0，

将(2)代入上式，

得(k2+1)(a2m2-a2b2)+(km-kt-s)(-2a2km)+(m2+s2+t2-2mt)(a2k2+b2)=0，

展开整理得(a2-b2)s2k2+2a2skm+(a2+b2)m2-2b2tm+(b2-a2)t2=0，

对其因式分解得(sk+m-t)[(a2-b2)sk+(a2+b2)m+(a2-b2)t]=0，

因为直线l不过定点(s,t)，则sk+m-t≠0，

于是(a2-b2)sk+(a2+b2)m+(a2-b2)t=0，

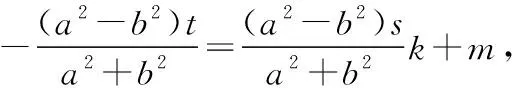
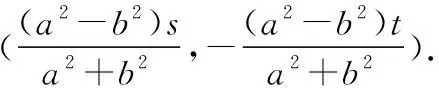
研究完椭圆，双曲线是否有类似的性质呢？于是得到：

不妨设直线l:y=kx+m，A(x1,y1),B(x2,y2)，

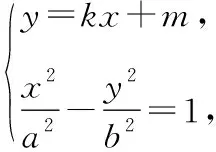
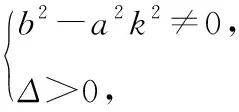
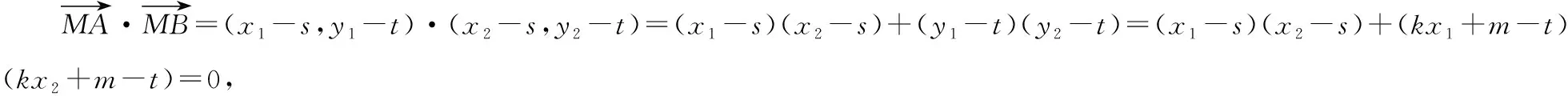
将(3)代入上式，

得(k2+1)(-a2m2-a2b2)+2a2km(km-kt-s)+(m2+s2+t2-2mt)(b2-a2k2)=0，

展开整理得(a2+b2)s2k2+2a2skm+(a2-b2)m2+2b2tm-(b2+a2)t2=0，对其因式分解得(sk+m-t)[(a2+b2)sk+(a2-b2)m+(a2+b2)t]=0，

因直线l不过定点(s,t)，则sk+m-t≠0，

于是(a2+b2)sk+(a2-b2)m+(a2+b2)t=0，

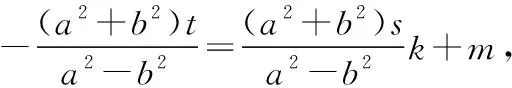
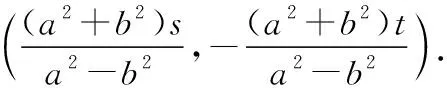
3.教学反思

高三学生的复习时间紧、任务重、压力大，如何提高每节课的复习效率是每一位高三教师必须面临和思考的问题，笔者认为要努力做到以下几点：

3.1重视教材中的例题、习题

高考命题立足于教材，不少试题直接来源于教材中的例题和习题，但不少师生并不重视教材的再利用，把教材丢到一边，都是以复习用书为主，先简单回顾知识点，接着就是讲解试题和练习.长此以往，学生必然对复习失去新鲜感，导致复习效率不高.高三的复习过程中，教材中的典型例题、习题，实际上就是“题根”，教师要充分挖掘其隐含的应用价值，引导学生回归教材，让学生体会到“书中自有黄金屋”.

3.2引导学生学会制定解决问题的路线图

本题的求解主要分两步，先根据数量积为0得到直线过定点的结论，再利用几何法或代数法求距离的最大值.其中第一步求得直线过定点是关键，在求解过程中注意联想特殊情况，即结论1，再进行类比，将数量积坐标化，得到直线过定点的结论.所以在遇见复杂问题时，要引导学生学会将其转化为简单问题，制定解决问题的路线图.从简单问题出发，相当于从“低处”着手，从“易处”着手，从“小处”着手，这样一来，试题起点就比较低，难度就不大，考查的知识点也较少，学生就能解决，让学生体会到成功的愉悦，增加学习的信心.教师在此基础上再开展变式教学，一题多变，一题多解，多题一解，引深引难，立意越来越高远，试题难度逐渐加大，所运用的知识点和思想方法越来越多，题型越来越丰富，于“润物无声”中提高学生的思维能力，提升学生的核心素养，真正提高高三复习课的效率.

3.3试卷讲评要有针对性