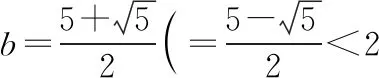二次函数在闭区间的最值问题研究

安徽 陈晓明

多年来二次函数在闭区间的最值问题一直是高考的热点问题，此类问题主要包括四种情况：轴定区间定(二次函数的对称轴和定义域都不含参数)；轴定区间动(只有定义域区间端点含参)；轴动区间定(只有二次函数的对称轴含参)；轴动区间动(二次函数的对称轴和定义域区间端点都含参数)．因为第一种情况较简单，第四种情况较复杂，所以考的较少，而中间两种情况考的特别多．“轴动区间定”的情况只需分三种情况讨论(轴在区间左、中、右)即可，难度也不大，因此本文主要研究“轴定区间动”的情况．巧合的是，本学期笔者所在学校(省级示范高中)的三次大型考试都考到了这种情况．在试卷讲评课上笔者带领学生对试题进行研究，以期找到此类问题的求解策略．

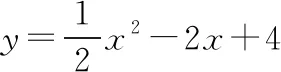
A.b=2 B.b≥2 C.12

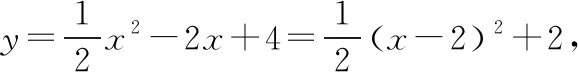
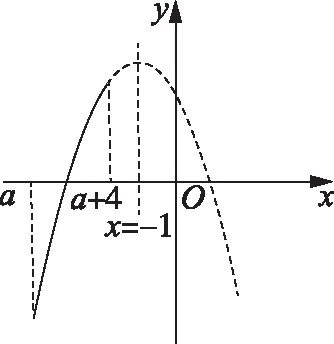
【例2】已知函数f(x)=-x2-2x+3，求函数f(x)在区间[a,a+4]上的最小值．

错解：如图所示，要求函数f(x)在区间[a,a+4]上的最小值，只需比较区间的端点离对称轴x=-1的远近即可．因此分3种情况讨论：

(1)当-1-a>(a+4)-(-1)，即a<-3时，函数f(x)的最小值f(x)min=f(a)=-a2-2a+3．

(2)当-1-a=(a+4)-(-1)，即a=-3时，函数f(x)的最小值f(x)min=f(a)=f(a+4)=-a2-2a+3=0．

(3)当-1-a<(a+4)-(-1)，即a>-3时，函数f(x)的最小值f(x)min=f(a+4)=-a2-10a-21．

剖析：能将求函数最值的问题转化为比较区间端点离对称轴远近的问题，体现了化归与转化及数形结合的思想，然后通过分类讨论解决问题．但是图象画的不够准确，因为定义域区间[a,a+4]长度为4，而抛物线f(x)=-x2-2x+3与x轴两交点分别为(-3,0),(1,0)，它们之间的距离也为4，而从图象上看[a,a+4]却落在[-3,1]的内部，明显不对．幸好还不影响解题．另外，如图所示，当对称轴x=-1在区间[a,a+4]右侧时，上面分类中的(a+4)-(-1)为负值，不能表示右端点到对称轴的距离．因此，上面的分类只是对称轴x=-1在区间[a,a+4]内的情况，还要讨论对称轴分别在区间左及区间右的情况．

(2)当-1≥a+4，即a≤-5时，f(x)min=f(a)=

-a2-2a+3．

(3)当a≥-1时，易知f(x)min=f(a+4)=-a2-10a-21．

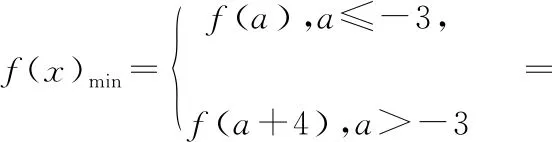
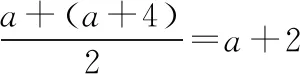
(1)当a+2<-1，即a<-3时，函数f(x)的最小值f(x)min=f(a)=-a2-2a+3．

(2)当a+2=-1，即a=-3时，函数f(x)的最小值f(x)min=f(a)=f(a+4)=-a2-2a+3=0．

(3)当a+2>-1，即a>-3时，函数f(x)的最小值f(x)min=f(a+4)=-a2-10a-21．

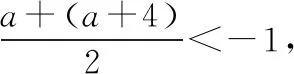
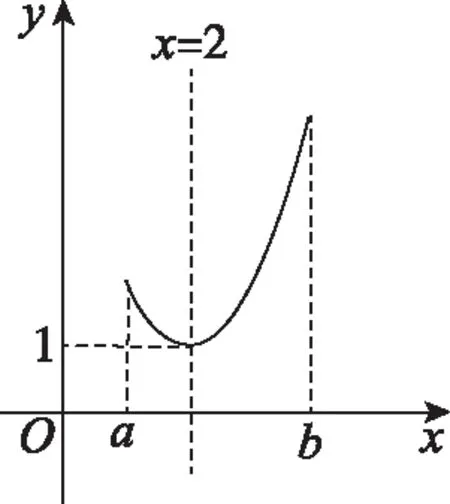
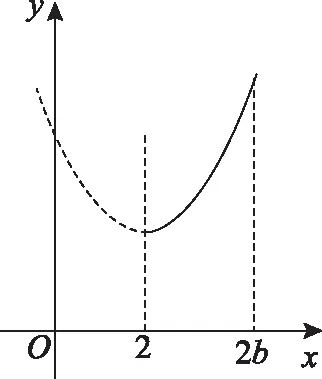
【例3】当x∈[a,b]时，函数f(x)=x2-4x+5的最小值为a，最大值为b，则b=________.

解析：本试题与前面试题有什么异同点呢？首先定义域区间有所不同，例1只有右端点含参，例2与例3左、右端点都含参，不同的是例2只含一个参数，而例3含两个参数．然后例1与例3其实都是定义域与值域相同(给出含参最值)，求参数的值．而例2是求含参最值．

本题还是要比较抛物线的对称轴x=2与定义域区间的位置关系.

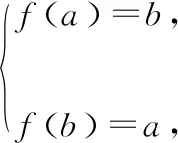
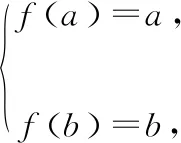
(3)当a<2

首先可以确定的是函数f(x)=x2-4x+5的最小值a=f(2)=1，这样函数的最大值b可分为两种情况：

①当b≤3时，如图所示，b=f(a)=f(1)=2，这与前提条件a<2

②当b>3时，如图所示，由题意知b=f(b)，故b2-

评注：看来研究二次函数在闭区间的最值问题，抓住抛物线的对称轴与定义域区间的位置关系进行分类讨论是解决问题的关键．这道在考场上得分率极低的试题并不是不可逾越的！

教学思考

通过前面的例题，我们不难发现试题难度在递进，学生在解题过程中会遇到一个个难以解决的问题．“问题探究”的学习方式对发展学生的思维有比较大的影响．学习数学，不只是学会数学知识，更重要的是学会数学式的思维，提高学生分析问题、解决问题的能力，培养学生的创新精神．这些仅凭学生听讲、做题是很难获得的，而以问题为中心的合作探究学习可以促进学生思维的飞跃、素养的提高．