盘点直线参数方程的主要应用
黑龙江 王荣峰
直线参数方程是普通高中课程标准实验教科书的重要内容,主要应用在求线段的长度、求距离的乘积、求直线的方程、求参数的取值、求参数的范围、求分点的坐标、求中点的轨迹和求面积的最值等问题中.
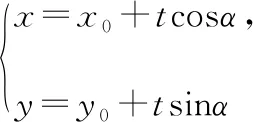
1.求线段的长度
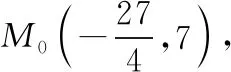
( )
A.1 B.3
C.4 D.5

点评本题也可写出直线l的点斜式方程,并与双曲线的方程联立,进而求出M点的坐标,最后由两点间距离公式来求解,但借助直线参数方程,利用参数t的几何意义来处理更显简洁清晰.
2.求距离的乘积

( )
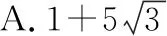
C.1或4 D.非上述答案


3.求直线的方程
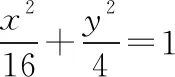
( )
A.x+2y-4=0 B.x-2y-4=0
C.2x-y-3=0 D.2x+y-3=0
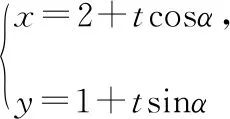
点评因为点M是线段AB的中点,由直线方程中参数t的几何意义可知t1+t2=0,于是便可求得tanα的值,进而找到了解决问题的突破口.
4.求参数的取值
例4.经过抛物线y2=2px(p>0)外的一点A(-2,-4),且倾斜角为45°的直线l与抛物线分别交于点M1,M2,若|AM1|,|M1M2|,|AM2|成等比数列,则实数p的值为
( )
A.1 B.4
C.1或4 D.非上述答案
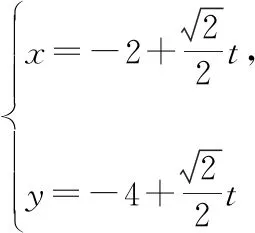
点评明确参数t的几何意义,并与二次方程根与系数的关系有机结合,便可使本题巧妙获解,增加了思维量,减少了计算量.
5.求参数的范围
例5.若抛物线y=ax2-1上始终存在关于直线x+y=0对称的两点A,B,则实数a的取值范围是
( )

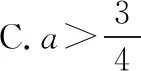


点评本题的解法有很多种,但巧设直线AB的参数方程,再借助参数t的几何意义和根与系数的关系可独辟蹊径,解题过程令人耳目一新.
6.求分点的坐标
例6.已知经过点P(2,9),斜率为2的直线l与圆x2+y2=50交于A,B两点,则线段AB的一个三等分点M的坐标为
( )
A.(-1,3)
B.(-3,-1)
C.(-1,3)或(-3,-1)
D.非上述答案

点评写出直线l的参数方程并通过解方程求出A,B两点对应的参数t1,t2,进而可求得三等分点M对应的参数t0,在求t0时类比了定比分点公式,充分体现出参数t作为“线坐标”的几何意义.
7.求中点的轨迹
例7.过点C(2,1)作直线l交双曲线x2-y2=1于A,B两点,则弦AB中点M的轨迹方程为
( )
A.y2-x2+2x+y=0 B.y2-x2-2x+y=0
C.x2-y2+2x+y=0 D.x2-y2-2x+y=0

点评写出直线AB的参数方程,则中点M对应的参数t0便可由参数α来表示,而消去α是解本题的难点和关键.同时,保持运算的等价性对数学素养提出了较高的要求.
8.求面积的最值

( )
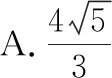
C.3 D.非上述答案




