例谈构造“模型”求解排列组合问题

江苏 于 健 郭建华

排列组合问题是高中数学的难点，因为问题都比较抽象，运用常规方法不容易迅速入手或者运算较为烦琐，若将抽象的排列、组合问题转译或构造为与其等价的数学模型或实际模型，恰当地运用模型加以处理，常会有化难为易、独辟蹊径之处．下面笔者就几类问题举例说明，以飨读者.

一、构造组合模型

点评：这种构造组合模型证明构思精巧，把枯燥抽象的公式还原为有意义的实例，既便于理解记忆，又能极大地激发学习兴趣．

二、构造隔板模型

所谓隔板法是指在n个相同元素间插入(m-1)个板，即把n个元素分成m部分的方法．其实就是将相同的球放入不同的盒子，每个盒子放入球的个数不限，求不同方法种数的一种解题方法．其中用球代表相同元素，用板所隔出的几个部分代表相应的分配集合，也就是“球”通过隔板的不同插入方式，得到不同的分配结果．

例3.把8个相同的小球放入4个不同的盒子，每个盒子至少有一个球，有多少种不同的放法?

解法1：因为球与球没有差别，但是盒子不一样，所以各盒子中小球数量的不同，就属于不同的放法．

解法2：第一步：在各盒子中先放一个小球，仅有1种放法；

所以把8个相同的球放入4个不同的盒子，每个盒子至少有一个球，有35种不同方法．

点评：因为球是一样的，盒子是不一样的，所以不同的放球方法体现在不同盒子中的球的个数的不同；解法1和解法2的第二步都运用了“隔板法”；解法2将问题解决分成了两步．

变式1：把8个相同的小球放入4个不同的盒子，有多少种不同的放法?

所以把8个相同的球放入4个不同的盒子，有165种不同放法．

变式2：方程x1+x2+x3+x4=8的非负整数解的组数是多少?

解析：把x1，x2，x3，x4看成4个不同的盒子，本问题可理解为将8个相同的小球放入4个不同的盒子(允许有空盒子)，与变式1属同一问题的不同表征(解略)．

点评：相同的球放入不同的盒子，每个盒子放球数不限，适合隔板法．隔板的块数要比盒子数少1．

例4.求(x1+x2+x3+x4+x5)10展开式中共有多少项?

所以(x1+x2+…+x5)10展开式中共有1 001项．

点评：准确理解隔板法的使用条件，是使用隔板法求(x1+x2+…+x5)10展开式中的项数的理论依据．

三、构造数列模型

例5.有一楼梯共10级，每步只能跨上1级或2级，问要登上最后一级共有多少种走法?

解析：因为每步只能跨上1级或2级，所以最后一步可能从第9级也可能从第8级跨上第10级，向前递推关系不变．设登上第k级有ak种走法，显然a1=1，a2=2，当k>2时，登上第k级台阶的走法可以分两种情况得到：从第k-1级台阶跨一级登上第k级，或从第k-2级台阶，一步跨两级登上第k级．故当k≥3时，有ak=ak-1+ak-2，

所以a10=a9+a8=2a8+a7=…=34a2+21a1=89.

点评：通过将实际问题抽象为数列模型进行问题解决，有利于培养数学抽象、逻辑推理等核心素养．

四、构造几何模型

例6.圆上有11个点，每两点连成一条线段，这些线段在圆内最多有多少个交点?以这些交点为顶点的三角形最多有多少个?

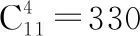
点评：该题如果用枚举法显然比较困难；同样用计数原理先算出弦的总数，然后算出交点，再减去圆外和圆上的交点个数也很困难．如果利用映射关系，那么可以起到化难为易的效果．

例7.如图，一个地区分为5个行政区域A，B，C，D，E，现给地图着色，要求相邻区域不得使用同一颜色，现有5种颜色可供使用，且每块区域只涂一种颜色，则不同的着色方法共有多少种?

解析：将其构造为四棱锥(如图)，题目即转化为用5种颜色对四棱锥的顶点着色，每相邻两点不同色．用分步计数原理按ABCDE的顺序着色，对A，B，C着色有5×4×3种，接下来对D和E着色，若D与B同色，接下来着色E，有1×3种，或者D与B不同色，接下来着色E，有2×2种，所以可得5×4×3×(1×3+2×2)=420种．

点评：本题若用常规方法，可以分为三类讨论：用5种颜色着色、4种颜色着色、3种颜色着色，运算复杂．恰当地构造几何模型，使问题大大简化，思维更为清晰，几何作为一种直观形象的数学模型，在发展学生的直观想象能力，培养学生的创新精神方面具有独特的价值．