数列不等式证明的解题策略

福建 黄清波

常见的数列不等式证明大多与数列求和或求积有关，这类题型一直是各类考试的热点，也是学生学习的难点.证明的过程中经常要用到放缩法或数学归纳法等难度较大的数学方法，需要学生有敏锐的数学观察力和熟练的转化能力，同时还要能够恰当的放缩，解题过程技巧性强且难以操控，对学生知识以及思维能力要求较高.本文以2019年高考数学浙江卷第20题为例，从多个视角去考量这类问题的求解策略，希望读者能够从中受到启发，选择适当的方法解决问题.

题目：设等差数列{an}的前n项和为Sn，a3=4，a4=S3.数列{bn}满足：对每个n∈N*，Sn+bn，Sn+1+bn，Sn+2+bn成等比数列.

(Ⅰ)求数列{an}，{bn}的通项公式；

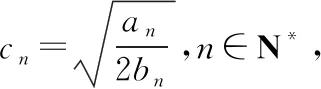
【分析】本题主要考查等差数列、等比数列、数列求和、不等式的证明等基础知识，考查推理论证能力、运算求解能力和综合运用能力，考查逻辑推理、数学运算等核心素养，难度较大.

策略一：数学归纳法

【分析】由于数列不等式与自然数有关，可优先考虑用数学归纳法.第一步，先验证n=1时，不等式成立；第二步，假设n=k(k∈N*)时不等式成立，充分利用假设，恰当放缩，证明n=k+1时不等式也成立.即证原不等式成立.

解法1:(Ⅰ)由已知条件易求得an=2n-2，n∈N*，bn=n2+n，n∈N*.

我们用数学归纳法证明.

(1)当n=1时，c1=0<2，不等式成立；

(2)假设n=k(k∈N*)时不等式成立，

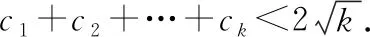
那么，当n=k+1时，

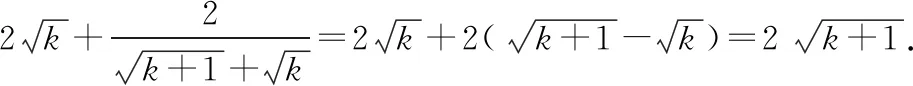
即当n=k+1时不等式也成立.

(Ⅰ)当n=1，2，3时，试比较f(n)与g(n)的大小关系；

(Ⅱ)猜想f(n)与g(n)的大小关系，并给出证明 .

解：(Ⅰ)当n=1时，f(1)=1，g(1)=1，所以f(1)=g(1)；

(Ⅱ)由(Ⅰ)猜想f(n)≤g(n)，下面用数学归纳法证明.

(1)当n=1，2，3时，不等式显然成立；

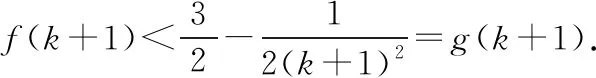
根据(1)和(2)可知，对任意n∈N*，都有f(n)≤g(n)成立.

策略二：分项比较法

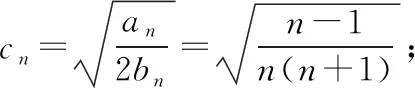
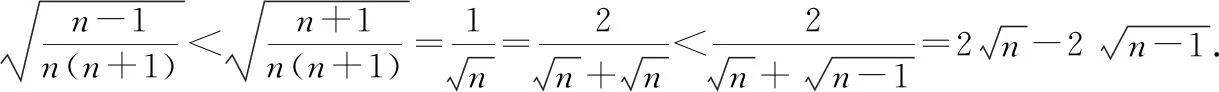
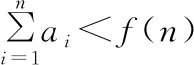
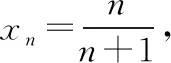
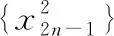
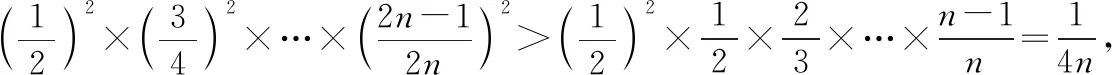
策略三：定积分法

【分析】求曲边梯形的面积是采用分割、近似代替、求和、取极限的方法，并由此抽象出定积分的概念，关键步骤是以小曲边梯形的面积近似值作为数列的项，再数列求和，把定积分与数列联系起来.