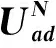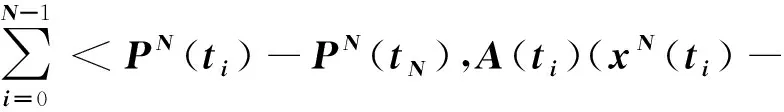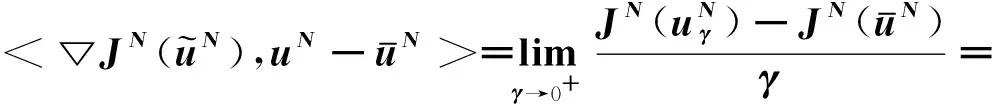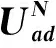Mayer型线性最优控制问题的一阶充分条件*

淳 黎， 王 彬

(四川师范大学 数学科学学院，成都 610068)

0 引 言

设A(·)∈C([0,T];Rn×n)，B(·)∈C([0,T];Rn×m);h:Rn→R为给定的一阶连续可微函数，Rn×m与Rn×n分别表示n×m与n×n阶矩阵全体，C([0,T];Rn×n)，C([0,T];Rn×m)表示Rn×n,Rn×m矩阵值连续映射全体，记平方可积函数空间L2(0,T;Rm)上的范数与内积分别为‖·‖2与[·,·]L2，记连续函数空间C([0,T];Rn) 上的范数为‖·‖∞，考虑线性控制系统 :

(1)

Mayer型性能指标:

J(u(·))=h(x(T))

其中：x(T)表示式(1)的解x在T时的值。设控制集U为Rm中的有界闭凸集，可行控制集Uad定义为

Uad:={u(·):[0,T]→U|u(·)Lebesgue可测}

(2)

上述最优控制问题广泛存在于实际工业生产中。求解这类最优控制问题的主要方法之一是求解最优控制的一阶必要条件[1]。然而，类似于微积分中求函数极值，最优控制的一阶必要条件并不一定是充分条件。为使得满足一阶必要条件的允许控制为最优控制，必须对最优控制问题施加适当的凸性条件。现有研究中，一阶充分条件中对最优控制系统的凸性要求比较苛刻，比如，对上述Mayer型问题通常要求函数h为凸函数[2-3]。过高的凸性要求使得相应的一阶充分条件只适用于结构比较特殊的最优控制问题，从而限制了利用一阶最优性条件求解最优控制这一方法的适用范围。本文在仅假设函数h为伪凸函数的条件下证明最优控制问题的一阶必要条件的充分性。因此，与已知一阶充分条件相比，文中所得的一阶充分性条件适用于更广泛的最优控制问题。作为应用，本文将原最优控制问题等价地转化为一阶必要条件对应的伪单调变分不等式问题，并利用处理伪单调变分不等式的一类双投影算法[4]给出最优控制的一个简单的数值算例。

1 预备知识

定义1[5]设X为Hilbert空间，其上赋予内积[·,·]X,h:X→R为一阶可微函数，若

h(y)>h(x)⟹[▽h(y),x-y]X<0,∀x,y∈X

则称h为定义在X上的伪凸函数。

定义2[5]设X为Hilbert空间,K为X中的非空闭凸子集，F:K→X称为

(i) 单调映射，若对任意x,y∈K,都有

[F(x)-F(y),x-y]X≥0

(ii) 伪单调映射，若对任意x,y∈K,都有

[F(y),x-y]X≥0⟹[F(x),x-y]X≥0

容易证明，凸函数的导函数为单调映射，伪凸函数的导函数为伪单调映射。

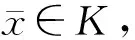
(3)

定义Hamilton函数：

H(t,x,u,P)=[P,A(t)x(·)+B(t)u(·)]

(4)

其中：(t,x,u,P)∈[0,T]×Rn×U×Rn。

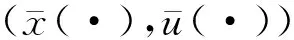
(5)

其中，P(·)称为伴随变量，其满足的方程称为伴随方程。

2 主要结果

下面，在函数h为伪凸函数的条件下证明一阶必要条件式(5)的充分性。

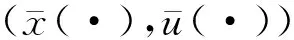
证明下面将分两步证明该结论。

第1步首先证明当h是Rn上的伪凸函数时，最优控制问题式(2)的性能指标J是关于控制u在Uad上的伪凸函数。

任取可行控制u1,u2∈Uad，设J(u1)

[▽h(x2(T)),x1(T)-x2(T)]<0

令xβ(·)为控制系统式(1)关于控制u2+β(u1-u2)的解。由控制系统式(1)的线性性，易知

xβ(·)-x2(·)=β(x1(·)-x2(·))

故由h的连续可微性及Lebesgue控制收敛定理得：

(6)

因此，由u1,u2的任意性及伪凸函数的定义可得性能指标J是关于u的伪凸函数。

(7)

的解。

类似于第一步的讨论，

(8)

设P(·)为一阶必要条件中伴随方程：

(9)

的解。由式(7)与式(9)的对偶关系，有

(10)

结合式(8)与式(10)可知

3 最优控制的数值解

设x(·;u)为式(1)中微分方程关于u(·)的解，P(·;u) 为式(5)中伴随方程关于u(·)和x(·;u)的解。定义映射F:Uad→L2(0,T;Rm)如下:

F(u)=-B(·)TP(·;u),∀u∈Uad

(11)

设t0=0,t1=Δt,…,ti=iΔt,…,tN=T,其中N为

uN:=(uN(t0)T,…,uN(tN-1)T)T
xN:=(xN(t0)T,…,xN(tN)T)T

由控制系统式(1)的Euler差分格式得：对i=0,…,N-1,有

(12)

若定义

(13)

由参考文献[8]中定理2可得如下收敛性结果：

类似于式(12)，记

PN:=(PN(t0)T,…,PN(tN)T)T

由倒向Euler差分格式，定义PN如下:

(14)

对给定的uN，利用式(12)与式(14)可定义映射FN:RNm→RNm如下：

(15)

(16)

容易证明式(16)是离散优化问题式(13)对应的一阶必要条件。利用定理2的证明方法并结合凸分析的知识容易证明如下结果：

其中，n=0,1,2,…,N。

下面，还是分两步来证明。

JN(x1(tN))

由h为伪凸函数，得

[▽h(x2(tN)),x1(tN)-x2(tN)]<0

另一方面，有

因此, 对∀n=0,1,2,…,N-1,有

因此有

设PN为差分方程式(14)的解，则

由于

因此

综上可得

另一方面， 若

则有

由JN(·)为伪凸函数，有

例1 设T=1，n=m=1，控制集U=[0,1]。考虑如下控制系统：

及性能指标

J(u(·))=ln(x(T))

致谢:非常感谢四川师范大学数学科学学院张海森老师对本文提供的指导和建议。