基于Smith预估型模糊PID温度控制系统的设计*

戴世纪, 王仲根

(安徽理工大学 电气与信息工程学院，安徽 淮南 232001)

0 引 言

PID算法是工业应用最广泛的算法之一，其中P是比例系数，I是积分系数、D是微分系数，同时通过反馈回路形成闭环控制系统，最能体现反馈思想的控制系统，具有结构简单、易于实现等优点，但在复杂工况的工业场景中难以取得预期的理想结果。为了在工业中广泛应用，许多科技人员开展大量研究。文献[1]设计一种常用的Fuzzy-PID算法控制系统温度，对PID整定值进行在线调整，使其具有较好的适应能力。文献[2]建立了模糊神经网络PID算法的结构模型，在模糊PID算法中引入神经网络模型，解决了系统纯滞后的问题，具有较强的鲁棒性。文献[3]通过粒子群算法得到PID系数，利用闭环负反馈的PID结构实现对系统的温度在线调整。文献[4]提出了一种综合滤波算法用来消除噪声对温度信号的干扰，对电压信号进行滤波消噪处理，利用综合滤波算法为基础并辅以模糊自适应PID控制温度，此方法可消除多数噪声。文献[5]方法通过蚁群算法获取一组最佳的PID系数Kp、Ki、Kd，具有良好寻优的特性，在规定范围内进行高效启发式搜索找到最优解。但上述控制系统操作复杂，成本较高，参数控制困难，难以在保证系统性能的前提下，提高操作可行性。

为提高温控系统性能，解决温控系统中产生超调量较大的扰动，响应时间较长等问题[7]。设计一种基于Fuzzy-Smith滞后补偿型PID温控系统，系统在一般PID算法上改进，将模糊推理环节加入PID控制中，并通过Smith算法减少系统的波动幅度，改善温控的稳态品质，降低响应时间，提高控制过程的鲁棒性[8]。

1 温度控制系统结构

1.1 室内温度控制模型

由于室内温度控制系统设计较为复杂，其延迟时间、增益系数和时间常数反映了温度控制的动态特性[9]。因此，室内温度模型的传递函数可表示为

(1)

式(1)中，K为增益参数，τ为时滞时间，T为时间常数。考虑实际情况，实验温度控制初值为18 ℃，根据Cohen-Coon整定法可得出K=1，T=10，τ=5，因此，函数的传递函数为

(2)

1.2 模糊控制规则

模糊控制通过事先设定的规则表使控制器由自我学习和组织的功能，以特定的语言变量建立映射关系，完成模糊推理，并将结果输出到控制器，规则表体现了系统的偏差值、偏差变化量与系统输出之间的映射[10]。控制流程如图1所示。

一般情况下，温度模糊控制系统选择预定温度和实际温度的偏差e及偏差变化率ec作为模糊控制器的输入，系统的决策部分选用的是Mamdani算法。规则库是由若干条控制规则组成，按照IF…is…and…is…THEN…is…的形式表达。根据实践经验，具体的系统规则如表1所示。

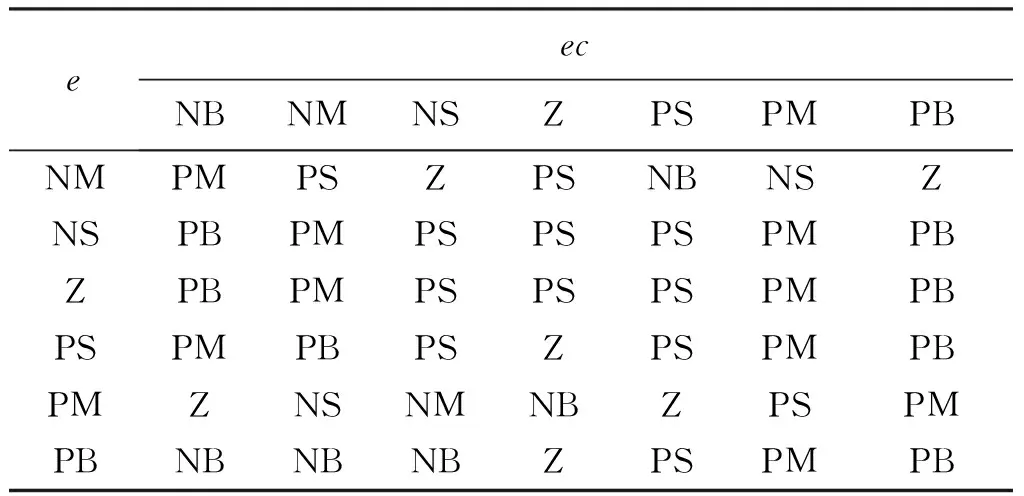
表1 Kd模糊控制规则表Table 1 Kd fuzzy control rule table

2 模糊PID及Smith预估器

2.1 模糊PID

模糊控制是基于模糊逻辑的描述一个过程的控制算法，缺点是难以消除稳态误差，稳态精度较低[11]。因此，在传统PID算法中引入模糊推理算法，加快响应速度，提高系统的稳定性，是一种常见的控制方法。具体传统PID控制流程如图2所示。

系统是两输入三输出的模糊控制结构，得到模糊推理的输出量是调整值ΔKp、ΔKi、ΔKd，通过将推理输出值代入以下公式，得出最佳PID调整值。如式(3)所示:

(3)

式(3)中，Kp为实际PID控制的参数，Kp0为PID的参数整定值，Gp为比例因子。计算机控制中常用的PID控制的表达式如式(4)所示：

(4)

式(4)中，Kp为比例参数，Ki为积分参数，Kd为微分参数。Kp能够提高系统的响应速度[12]。Ki可以消除系统的稳态误差。Kd用来增强系统的动态特性，对系统偏差进行预报。

2.2 Smith预估器控制

Smith算法是一种对滞后环节预判的时延补偿算法。其主要思想是被控对象包含着纯滞后环节，使系统调节能力下降，一般PID算法不能取得良好的效果。在此情况下，加入含有滞后部分G(s)(1-e-τs)的Smith补偿型算法，以降低被控系统的震荡幅度，克服了一般PID算法的缺陷，加快响应速度。其控制流程如图3所示。

由图3的流程图可知，含有滞后补偿的反馈回路与Smith算法结合的闭环函数表达式如式(5)所示：

(5)

式(5)中Gc(s)为系统函数表达式，Gp(s)e-τs含有纯滞后被控系统的函数式。在式中系统存在着延时特性e-τs，为了克服系统的延时特性，在控制系统的回路中加入补偿环节Gp(s)e-τs，使系统过程提前了τ时刻，消除了系统的纯滞后环节e-τs部分，即经过了预估补偿。因此，通过与时延补偿环节结合后，闭环回路的函数表达式转化为式(6)所示：

(6)

将模糊控制引入Smith预估控制中，并在反馈回路上加入Smith预估器用于提前预测调整系统的超调量，构成Smith-Fuzzy控制系统。其流程如图4所示。

3 系统仿真及结果分析

3.1 仿真过程

基于Matlab建立温控仿真系统，设置目标温度为20 ℃，系统时间为200 s。其中，模糊控制的输入系数Ke=0.01，Kec=4，模糊控制的输出系数分别为Gp=0.01，Gi=0.001 5，Gd=0.003 5，PID控制器的整定初始参数为Kp0=0.82，Ki0=0.13，Kd0=1。其中常规PID控制仿真如图5所示。

为了比较Fuzzy-Smith算法优化后的效果，将其与Fuzzy-PID算法、一般PID算法和Smith型PID控制进行比较，4种控制方案如图6所示。

3.2 结果分析

实验结果如图7所示，一般PID算法温度最大值为25.7 ℃，震荡幅度为28.5%，响应时间约115 s后达到稳定；Fuzzy-PID算法的最高温度为23.6 ℃，震荡幅度为18%，响应时间约105 s后温度达到稳定；Smith算法的温度没有明显的振荡产生，响应时间约为70 s后温度达到稳定；Fuzzy-Smith控制温度的最高温度20.8 ℃，振荡幅度仅为4%左右，调节时间约为60 s后温度达到稳定值。

通过对结果分析可知，传统的PID算法和模糊PID算法的上升速度较快，但超调量较大，系统稳态误差较大，适应力较弱，调节能力较差；Smith算法的超调量相比其他算法小，能够使系统保持较好的鲁棒性，但曲线上升时间和系统调节时间较慢。Fuzzy-Smith算法的温度上升较快，振荡幅度相比其他控制方法较小，几乎可以不记，而调节到稳定温度值所花时间较少，可以明显改善温控系统的性能，增强调节能力和抗干扰能力，曲线上升时间快，时间延时短、具有比较理想的稳态品质。具体参数性能由表2可以看出。

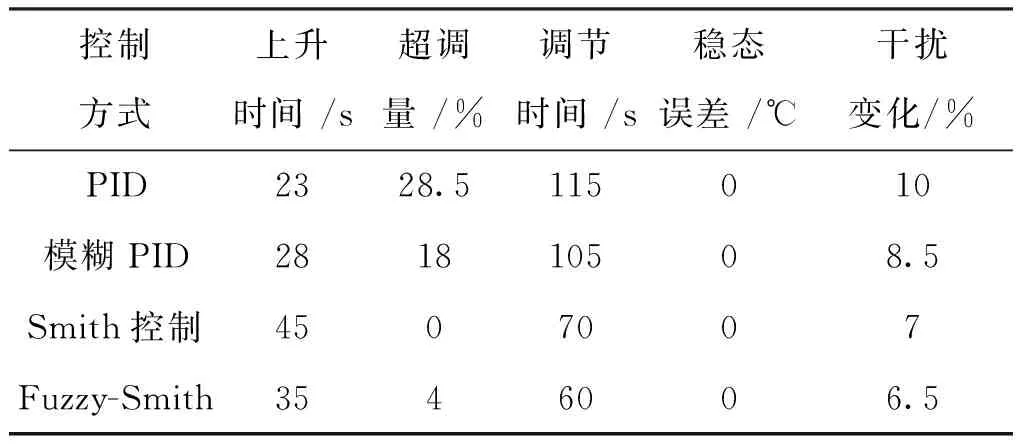
表2 4种算法调节结果Table 2 Four algorithms adjustment results

3.3 系统抗干扰能力分析

为了比较系统在不同情况下的抗干扰能力，在T=85～90 s处预先在PID控制系统中加入一个幅值为4的阶跃干扰信号，仿真结果如图8所示。图8可以看出：4种控制系统受到干扰后都产生了1次明显振荡，其中模糊PID控制系统受干扰后产生较大的曲线波动，受到干扰影响较强，最大波峰变化量为8.5%，而模糊Smith-PID控制受到阶跃干扰信号较小，最大波峰变化量仅为6.5%，保持了较好的稳定性和控制精度，具有良好的抗干扰性能。

4 结 论

建立了室内温控系统的数学模型，针对室内温度控制系统具有调节弱、纯滞后和非线性的特点，提出一种基于Fuzzy-Smith补偿型的PID控制算法。实验结果表明，Fuzzy-Smith型算法充分发挥了Smith算法的滞后补偿作用，与其他方法相比，Fuzzy-Smith控制系统能够抑制系统的超调量，加快调节响应速率，通过对控制系统时滞性进行补偿提高控制对象的稳态特性，同时还具有模糊推理方法的优势，达到预期的系统特性。