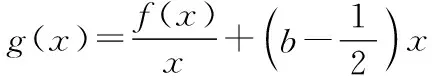教学考试杂志社“优师计划”阶段性成果展示——高考重难点相关试题选登

1.已知某函数的图象如图所示,则该函数的解析式可能是

( )

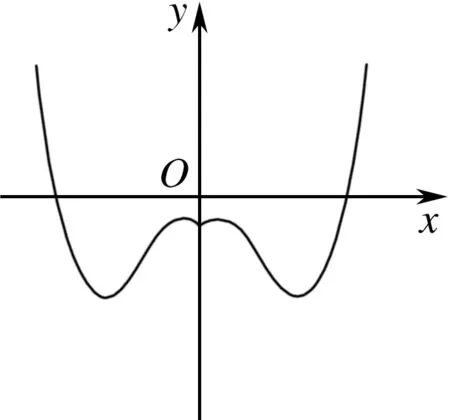
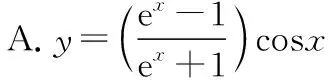
C.y=2x-|x|+2 D.y=(x2-1)cosx

【答案】B

( )

A.200π-5 B.200π+5

C.210π-5 D.210π+2

【答案】C

( )

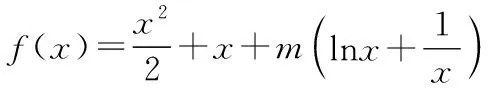
A.m>0 B.m≤1

C.m>1 D.m≤0

【答案】A

( )

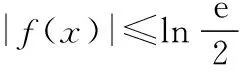
A.(0,ln2]

B.(-∞,-ln2]∪[ln2,+∞)

C.(-∞,ln2]

D.[-ln2,ln2]

【答案】D

( )

A.(-∞,1) B.(-∞,1]

C.(0,+∞) D.[1,+∞)

【答案】B

( )

A.(-1,0) B.(0,1)

C.(-∞,-1) D.[1,+∞)

【答案】C

7.函数f(x)=x3-5x2+3x+9与x轴交点的个数为

( )

A.0 B.1 C.2 D.3

【答案】C

( )

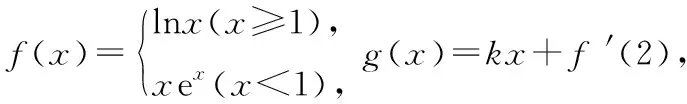
【答案】D

9.曲线f(x)=x3-2x，在点A处的切线平行于直线y=x+1,则A点坐标为________.

【答案】(1，-1)或(-1,1)

12.当直线y=kx+b同时与曲线y=ex和y=ln(x+2)相切时,b=________.

13.(本小题满分12分)

已知f(x)=mlnx-2x(m>0).

(Ⅰ)若∀x>0,都有f(x)≤0,求m的取值范围;

(Ⅱ)若m=1,曲线y=f(x)上的点(x0,y0)(x0>0)处的切线l与y=x2相切,求满足条件的x0的个数.

【解题分析】(Ⅰ)由f(x)=mlnx-2x，

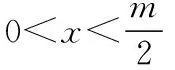
再由m>0可得0

即m的取值范围为(0,2e].

(Ⅱ)当m=1时,y=lnx-2x,

令g(x)=4x2lnx-4x+1,

则g′(x)=8xlnx+4x-4,

令h(x)=8xlnx+4x-4,

则h′(x)=8lnx+12,

则h(x)=x(8lnx+4)-4

∴当0

当x>1时,h(x)>0,即g′(x)>0，

即g(x)在(0,1)上单调递减,在(1,+∞)上单调递增,

∴当x=1时,g(x)取得极小值g(1)=-3<0.

又g(0)=1>0,且g(e)=4e2-4e+1>0.

∴g(x)=0在(0,1)和(1,+∞)上各有1个零点.

14.(本小题满分12分)

已知函数f(x)=(x2+a)ex-a(x+1).

(Ⅰ)当a=0时，求函数f(x)在(1,f(1))处的切线方程；

(Ⅱ)若a≥-2，证明：当x≥0时，f(x)≥0.

【解题分析】(Ⅰ)当a=0时,f(x)=x2ex,f′(x)=(x2+2x)ex,f′(1)=3e,f(1)=e.

∴函数f(x)在(1,f(1))处的切线方程为

y-e=3e(x-1)，即3ex-y-2e=0.

(Ⅱ)证明:f′(x)=(x2+2x+a)ex-a,

令g(x)=f′(x)，

则g′(x)=(x2+4x+a+2)ex.

∵a≥-2,

∴当x≥0时，(x2+4x+a+2)ex≥(x2+4x)ex≥0，

即g′(x)≥0,

∴g(x)在[0,+∞)上是增函数，

故g(x)≥g(0)=0，即f′(x)≥0,

∴f(x)在[0,+∞)上是增函数,

∴f(x)≥f(0)=0，

故若a≥-2，当x≥0时，f(x)≥0.

15.(本小题满分12分)

(Ⅰ)求函数f(x)的单调区间和极值；

【解题分析】(Ⅰ)由题意可知，函数f(x)的定义域为(0,+∞)，

①当a+1≤0,即a≤-1时,f′(x)≤0,

所以函数f(x)的单调递减区间为(0,+∞),没有极值；

②当a+1>0,即a>-1时,

由f′(x)=0，解得x=a+1,

当00,

当x>a+1时,f′(x)<0，

所以函数f(x)的单调递增区间为(0,a+1),单调递减区间为(a+1,+∞)，函数f(x)有极大值,没有极小值，

F(x)=-bxlnx+x2+b+1在[1,e]上有零点，

即方程-bxlnx+x2+b+1=0在[1,e]上有实根,

①当b+1≤1,即b≤0,x∈[1,e]时,h′(x)≥0,h(x)在[1,e]上单调递增,

②当1

x∈[1,b+1]时,h′(x)≤0,h(x)单调递减,

x∈[b+1,e]时,h′(x)≥0,h(x)单调递增,

所以h(x)min=h(b+1)=2+b-bln(b+1),

由1

所以h(b+1)>2,

则h(x)=0在[1,e]上没有实根.

③当b+1≥e,即b≥e-1,x∈[1,e]时,h′(x)≤0,h(x)在[1,e]上单调递减,

16.(本小题满分12分)

(Ⅰ)讨论f(x)的单调性;

【解题分析】(1)f(x)的定义域为(0，+∞)，

当a≥0，x∈(0,2)时,f′(x)<0;

当x∈(2,+∞)时，f′(x)>0，

此时，f(x)在(0,2)上单调递减，在(2,+∞)上单调递增.

当a<0时，令f′(x)=0,解得x1=-a,x2=2.

①当-a<2，x∈(0,-a)∪(2，+∞)时，

f′(x)>0;当x∈(-a,2)时，f′(x)<0,

此时f(x)在(0,-a)和(2,+∞)上单调递增，

在(-a,2)上单调递减;

②当-a>2时，x∈(0,2)∪(-a,+∞)时，f′(x)>0;

x∈(2,-a)时，f′(x)<0,

此时f(x)在(0,2)和(-a,+∞)上单调递增，

在(2,-a)上单调递减;

此时f(x)在(0,+∞)上单调递增.

令h′(t)=0，则t=e,当t∈(0,e)时,h′(t)>0;

如图可知:

①当b≤0时，h(t)有唯一一个零点，

即g(x)有唯一一个零点;

即g(x)有两个零点;

即g(x)有唯一一个零点;

即g(x)此时无零点.