展示过程 启发探究 递进生长——基于对数学二轮复习教学的几点认识

湖南 欧阳才学

数学教学是数学思维活动过程的教学，课堂教学是学生获取数学知识、提高数学思维能力、形成数学核心素养以及良好数学思维能力最重要的途径.在数学二轮复习中，如何使我们的数学教学生成最大的效益？为此，笔者从如下几方面谈谈对数学二轮复习教学的认识.

一、二轮复习教学应体现“过程性”

数学教学是师生之间、学生之间交往互动与共同发展的过程.因此，即使在时间十分紧迫的二轮复习中，也要引导学生寻求知识产生的起因，让学生看到思维过程、主动参与知识的发现并探索它与其他事物的联系.让学生在探索过程中形成概念、寻求规律、获得结论，这是提高学生学习积极性和发展其数学能力的有效措施.课堂是二轮复习的主阵地，数学课堂教学包含数学知识(概念)教学和数学解题的教学，因此二轮复习中应做好以下两方面的工作.

1.数学概念的复习应是过程的复习

数学概念是反映现实世界数量关系和空间形式本质属性的思维形式，它是整个数学知识的基础，是数学思想方法的载体.数学二轮复习离不开概念的复习，数学概念的复习不应是“结论”的复习，而应是“过程”的复习.在二轮复习中，要把概念的形成与发展过程展现给学生，弄清概念的来龙去脉，从而理解概念的本质.

例1.复习双曲线定义时，依据定义中的关键词“绝对值”“常数”“小于|F1F2|”，为使学生有比较深刻的认识和理解，为学生设计了下面的“过程式”复习：将定义中的“小于|F1F2|”换为“等于|F1F2|”，其余条件不变，点的轨迹是什么？将定义中的“小于|F1F2|”换为“大于|F1F2|”，其余条件不变，点的轨迹是什么？将定义中的“绝对值”去掉，其余条件不变，点的轨迹是什么？令“常数”等于零，其余条件不变，点的轨迹是什么？将“小于|F1F2|”去掉，其余条件不变，点的轨迹是什么？

通过这样的“过程”复习，使学生模糊的认识逐渐清晰，加深了对双曲线定义的理解，从而在审题中不被“形”迷惑，能透过“形”，让学生发现问题本质.

2.在解题中应展示数学思维的形成过程

二轮复习也离不开解题教学.数学“解题教学”应是“过程”的教学，在解题的过程中，教师不能只告诉学生每一步如何做，而是要把为什么这么做的“思路历程”展现给学生，让学生经历一次探索并解决问题的过程，教会学生如何通过自己的分析获得解题思路.

一个注意展示思维过程的“解题教学”是这样的：

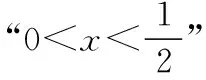
也就是说利用我们熟悉的“一元二次方程根的存在性与分布问题”已经解决了这个问题.

拓展：一般地，求分母为二次式的分式函数的最值，可以将待求的函数值先看成常数，再把分式函数转化成二次方程，利用判别式法解决.

二、二轮复习应突出“探究性”

古希腊生物学家罗塔戈说过：“头脑不是一个要被填满的容器，而是一个需被点燃的火把”.德国教育家第斯多惠也有一句名言：“一个坏的教师奉送真理，一个好的教师则教人发现真理”.由此，二轮复习不应是“灌输式”的，而应是“探究式”的复习；教师不应是“灌输者”，而应是“点火者”.教师在指导学生复习的过程中，应多为学生创设问题情境，启发学生思考和探究，激发学生的学习积极性，将教学过程变为师生共同探索知识的过程，帮助学生在自主探索和合作交流的过程中真正理解和掌握基本的数学知识与技能、数学思想与方法，从而获得大量的数学活动经验.

例3.(人教A版数学必修5第69页B组第6题)已知数列{an}中，a1=5，a2=2,an=2an-1+3an-2(n≥3)，对于这个数列的递推公式作一研究，能否写出它的通项公式？

多数与之配套使用的教辅书籍给出的解答是：

解法1.由an=2an-1+3an-2(n≥3)，得an+an-1=3(an-1+an-2),an-3an-1=-(an-1-3an-2).

又因为a1=5,a2=2，

所以an+an-1=3n-2(a2+a1)=7·3n-2，

an-3an-1=(-1)n-2(a2-3a1)=13·(-1)n-1.

由以上两式，得4an=3n-1×7+(-1)n-1×13.

上述解答中，为什么得到“an+an-1=3(an-1+an-2),an-3an-1=-(an-1-3an-2)”这两个关系式，让人感到“突兀”，我们只能当成是“观察”出来的.为了易于大家接受，下面探究了求解这类数列问题的一种通用方法：

所以an+an-1=3(an-1+an-2),an-3an-1=-(an-1-3an-2).

又a1=5，a2=2,

所以an+an-1=3n-2(a2+a1)=7·3n-2,

an-3an-1=(-1)n-2(a2-3a1)=13·(-1)n-1.

由以上两式，得4an=3n-1×7+(-1)n-1×13.

这一方法我们可以拓展到递推公式形如an=pan-1+qan-2(n≥3)的“双项递推数列”求{an}通项公式的一类问题：

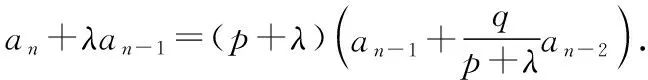
三、二轮复习应落脚“生长性”

波利亚有句名言：“掌握数学就是意味着善于解题.”解题是数学二轮复习的核心.提高解题效率的前提是教师做好例题和习题的设计.在设计时，教师首先要认真分析教材和学情，理清复习内容的结构，然后精心筛选和设计，并用合适的方式展开，变“罗列式”为“生长式”，由浅入深，逐步生长，组成一个有机的整体，凸显典型性、层次性、变化性和有效性.

二轮复习中要深刻挖掘例题和习题的教育功能，通过对原题进行适当变式，递进生长，延伸出具有相关性、相似性和相反性的新问题.这样，不仅能激发学生的思维，为学生展现出“活生生”的思维过程，还能有效地培养学生思维的深刻性、广阔性、独创性和灵活性，更能有效地提高学生发现和提出问题、分析和解决问题的能力.

解析完该题后进行了下面的变式.

通过对课本题目及变式的分析，归纳出了以下规律：平面内的动点到定点A(-a,0),B(a,0)的斜率乘积等于常数m(m≠0,-1)的点的轨迹是椭圆或双曲线;当常数m<0且m≠-1时，轨迹是除去两个定点A,B的椭圆；当常数m>0时，轨迹是除去两个定点A,B的双曲线.其中两个定点分别是椭圆或双曲线的顶点.从而使学生的思维得到了升华.