探究数形结合在高考数学函数解答题中的应用
甘肃 王新宏
我国著名数学家华罗庚曾作诗形容数形结合的思想方法:“数缺形时少直观,形缺数时难入微,数形结合百般好,数形分离万事休.”函数解析式与其图象建立了一一对应关系,使得数与形的研究可以相互转化,高考命题者将充分利用函数解答题的这一特点,考查考生能否将复杂的函数问题转化为借助直观的几何图形来解决问题的能力.
【例1】(2019·全国卷Ⅲ理·20)已知函数f(x)=2x3-ax2+b.
(1)讨论f(x)的单调性;
(2)是否存在a,b,使得f(x)在区间[0,1]上的最小值为-1且最大值为1?若存在,求出a,b的所有值;若不存在,说明理由.
【分析】(1)求出f′(x)=0的两根,比较两个的大小,结合f′(x)的图象草图,分情况讨论函数f(x)的单调性;(2)根据f′(x)与f(x)的图象草图,利用函数f(x)在x∈[0,1]的单调性,进行最大值和最小值的判断,最终得出a,b的值.
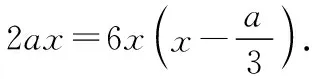
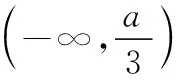

图1

图2
②当a=0时,函数f′(x)的图象草图如图3所示,函数f(x)在(-∞,+∞)上单调递增;
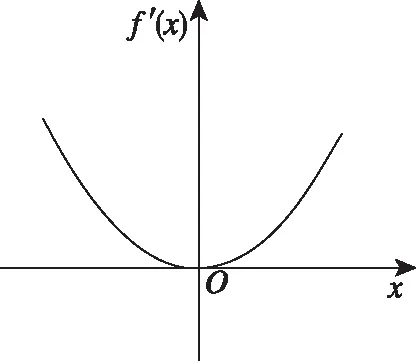
图3

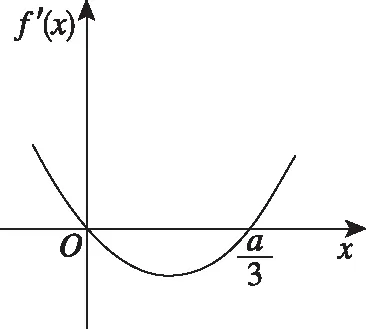
图4
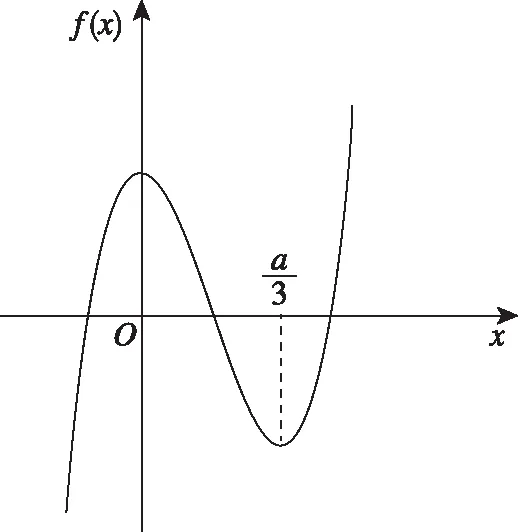
图5
(2)存在a,b,使得函数f(x)在区间[0,1]上有最大值1和最小值-1.
①若a<0,函数f(x)的图象草图如图2所示,此时函数f(x)在区间[0,1]上单调递增,所以f(0)=-1,f(1)=1代入解得b=-1,a=0,与a<0矛盾,所以a<0不成立;
②若a=0,函数f(x)在(-∞,+∞)上单调递增;所以f(0)=-1,f(1)=1,代入解得a=0,b=-1,符合要求;
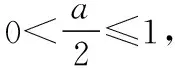


图6
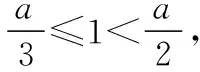

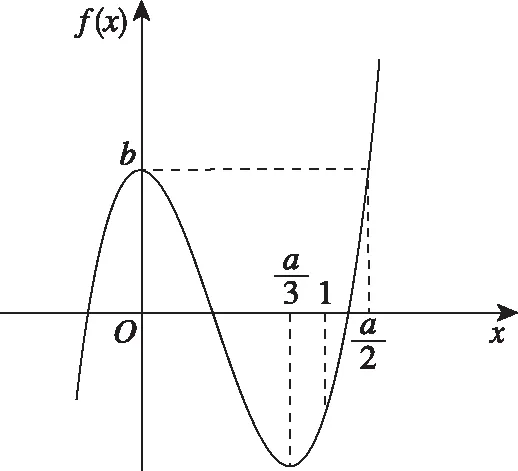
图7
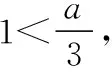

图8

②做函数解答题时,一边做题,一边思考图形,画出与之匹配的图形,通过图形,看透问题实质,指引着我们解题的方向,事半功倍,所以数形结合百般好,以形助数效率高.
【例2】(2019·全国卷Ⅰ理·20)已知函数f(x)=sinx-ln(1+x),f′(x)为f(x)的导数.证明:
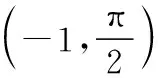
(2)f(x)有且仅有2个零点.
【分析】(1)写出f′(x)的表达式,利用其导函数f″(x)来研究f′(x)的单调性与极值点.
(2)以x为主元进行分类讨论,分别在各个区间上,由导函数的单调性以及特殊点的f′(x)的值来判断f′(x)与0的关系,得到f(x)的单调性,从而得到在各个区间的零点个数.
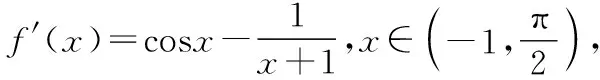

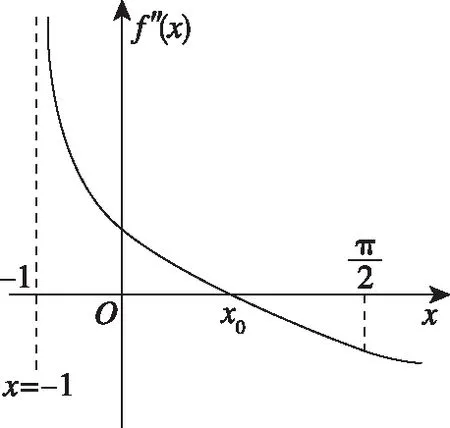
图9
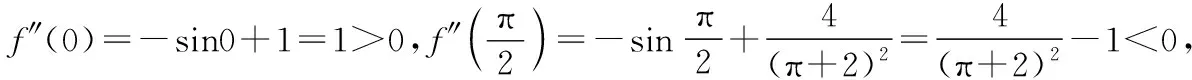
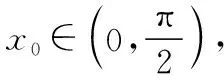

图10
【点评】含有对数函数、指数函数、三角函数与多项式函数的方程称为超越方程,超越方程我们是没有办法求解的,但高考函数解答题中f′(x)=0(或f″(x0)=0)的方程往往都是超越方程,此时我们常用的策略有两种:
①二次求导,即对y=f′(x)函数再次求导,二阶导函数y=f″(x)的正负对应着y=f′(x)的增减性,进而得出导函数y=f′(x)的正负情况,最终确定原函数y=f(x)的增减情况;
②设而不求,即先分析导函数(或二阶导函数)的单调性,判断它是否存在零点,若存在,再结合零点存在定理判断零点的个数,进而设出零点,对问题进行求解.
①当x∈(-1,0]时,由草图10可知f′(x)在(-1,0]上单调递增,所以f′(x)≤f′(0)=0即f(x)在(-1,0]上单调递减,又f(0)=0,所以x=0为函数f(x)在(-1,0]上的唯一零点;

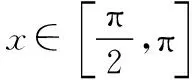

图11
④当x∈(π,+∞)时,函数f(x)的图象草图如图11所示,sinx∈[-1,1],ln(x+1)>ln(π+1)>lne=1,所以sinx-ln(x+1)<0,即f(x)在(π,+∞)上不存在零点.
综上所述,f(x)有且仅有2个零点.
【点评】数形结合可以很好地为解题探究思路,但不能用形的直观代替相关的计算与推理,画图不能太草,要尽可能准确,要善于用单调性、特殊点、特殊的数来准确定位图形的位置关系,帮助我们顺利解题.
数形结合是求解数学问题重要的思想方法,使用这种方法,很多问题迎刃而解,且解法简捷,特别是在函数解答题中发挥着巨大的作用,在求解过程中,图形可帮助我们找到解决问题的突破口,指引我们解题的方向,通过数与形的结合,会使复杂问题直观化、简单化,使解题的过程顺畅自然,水到渠成.

