一道三角问题的多解切入与思考

江西 黄邦活

“八仙过海，各显神通”，很多数学问题都可以从不同角度去思考，从有限的信息中寻找切入点，架设合适的桥梁，开拓解题思路，将问题转化为我们熟知的易于解答的新问题，来实现对原问题的解答，得到解题的有效方法.

【问题提出】

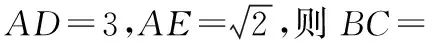
【问题分析】

1.根据AD=3,如何得到关于b,c的关系式？

切入点1：考虑平面几何知识，根据对角线互相平分，补成平行四边形，由余弦定理列式.

因为BD=CD，所以点D是BC的中点，如图所示，延长AD至F，使得AD=DF，则ABFC是平行四边形，则AF=2AD=6，∠ABF=180°-∠CAB=60°.

在△BAF中，由余弦定理得AF2=AB2+BF2-2AB·BFcos∠ABF,得b2+c2-bc=36.

切入点2：通过建立直角坐标系，设出相关点的坐标，由两点间的距离公式来列式.

整理得b2+c2-bc=36.

切入点1：由于AE是△ABC的角平分线，可以考虑角平分线定理中的线段比例关系，根据边角关系及余弦定理，建立等量关系.

因为∠BAC=120°，所以∠BAE=∠CAE=60°.

切入点2：建立直角坐标系，由B,E,C三点共线得到点E的坐标后，根据两点间的距离公式列出等量关系.

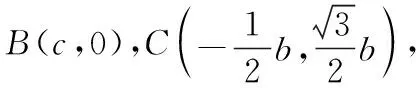
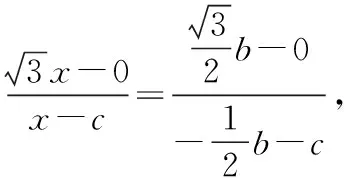
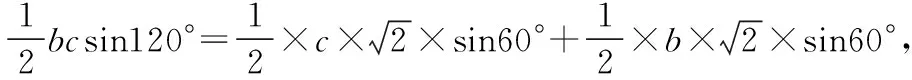
3.根据1,2的结论，又如何求BC呢？

切入点：因为在△ABC中有BC2=b2+c2+bc，若联立1,2中的结论通过解方程组解得b,c，计算麻烦，若观察待求式子的结构，整理处理，只需要分别得到b2+c2，bc便可以迎刃而解了.

整理得(bc)2-6bc-72=0，解得bc=12，

从而b2+c2=bc+36=48，

【题后思考】

1.总结解题规律，提炼解题方法

同一类型的问题，解题方法往往有其规律，当一个问题解决后，应认真总结，从解决问题中找出普遍适应的内容，以现在解决问题的经验帮助我们后续的问题解决.

从以上问题的分析与解答，我们可以看出：对于与三角形有关的问题，一是可以直接由正弦定理、余弦定理以及面积公式求解；二是可以运用平面向量的基底思想，转化为向量的数量积、夹角与模来运算；三是通过建立平面直角坐标系，运用解析法求解；四是利用图形的几何特征，通过补形与切割求解.

比较解法，可以得出：涉及三角形的中线长度，利用向量法，“单刀直入”，由向量运算与模之间的转化，可以快速求解；涉及三角形的角平分线长度，利用角平分线将三角形分割成两个小三角形，利用面积之间的等量关系，以及三角形的面积公式，则运算简单而快捷.

2.运用问题变式，提升数学思维

题海战术往往是“以多胜少”“就题论题”，在长期的题海训练中会身心疲惫，学生的学习会逐渐步入“低效率、重负担、低质量”的恶性循环中.适当通过不同角度、层次、情境进行变式训练，不仅可以克服这些缺点，而且可以做到方法归纳，题目归类，寻找数学问题本质特征，发现规律，开拓解题思路，突破思维束缚，形成良好的思维品质，真正增强学生的解题能力，从而达到举一反三、触类旁通的效果.

解答问题之后，我们可以变更结论与条件，从三角形边角、中线、角平分线、垂线、面积中选取变更条件，可以设置如下变式：

变式4在△ABC中，∠BAC=120°，D为边BC上的点，且BD=CD，若AD=3，则△ABC的面积的最大值为________.

变式5在△ABC中，角A,B,C所对的边分别为a,b,c，∠ABC=120°，∠ABC的平分线交AC于点D，且BD=1，则4a+c的最小值为________.

3.回归重视教材，发挥典例功能

我们知道，精心构思的教材习题，不仅是学习的内容，也是重要结论、命题、定理或数学思想的载体，更是编拟各类试题的源泉.因此，不少高考数学试题题目及思想“取材于教材，但又不拘泥于教材”，在典型问题身上往往能找到它们的“基因”，通过变形、改编与组合重组，展现典型问题的“魅力”.因此，随着高考的临近，应回归教材，重视教材，发挥教材中习题的功能，通过对教材中问题的适当拓展或延伸，改变题目的呈现形式，实现习题的推陈出新，充分发挥课本习题作为试题的根本来源的功能，以不变应万变，提高复习效率.如以上问题，可以是2019年北师大版教材高中必修四第82页例3、高中必修五第57页B组第1题的结论应用、解题方法的延伸，若能正确运用，解题会事半功倍.

不能只是为了解决数学问题而解数学问题，更重要的是理清解决数学问题的思路，掌握解决数学问题中的思维方式，总结规律，提炼方法，拓展延伸，同时也要重视回归教材，发挥习题的功能，这样才能触类旁通，举一反三，更有效地提高解题能力.