重视数学现象 探究数学本质

杨芳燕

(江苏省苏州湾实验初级中学 215200)

一、重视数学现象，探究概念本源

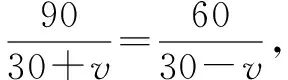
以上述分式方程求解过程为例：

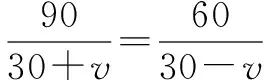
两边乘(30+v)(30-v)，

得90(30-v)=60(30+v)，

解得v=6.

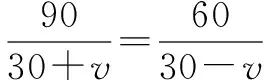
总结：通过教学情境引入课堂，教师不急于给出分式方程定义，通过教学现象引导学生用已有的知识结构自己探索，最后得出概念，从而探索了数学本源问题.

二、重视数学现象，将生活场景引入概念新知教学

教师在教学过程中要有意识地将所要学习的新概念与学生所生活的实际场景相结合，充分考虑学生实际的生活场景，利用学生在日常生活中常见的生活实例，提供现实原型，将抽象化的数学概念近乎形象化，从而激发学生学习的兴趣和学习期望，产生自行学习的内在动力.

以初中数学九年级上册“一元二次方程”教学为例，教师在上课之前，可以实现创设几个问题情境，学生讨论数学现象， 教师引导学生利用列方程的形式表示下列问题：“1.正方形的面积是9cm2，它的边长大小为x；2.一个面积为35的矩形泳池，其内部被分为一个边长为x的正方形，还有一个宽为x，长为3米的长方形休息区.”让学生自主思考，列出等式.(问题1答案为x2=9；问题2答案为x2+3x=35)基于一元一次方程知识背景，学生就很容易类比推理出一元二次方程的概念：含有一个未知数并且未知数的最高次数是二次的方程叫做一元二次方程.随后教师就可以轻松地引出一元二次方程的一般形式：ax2+bx2+c=0(a≠0)内容教学，让学生感受“数学，就是来源于生活”的特点.

三、经历概念生成，加深概念理解

1.基于学生的认知特点选择适当的教学策略揭示数学概念间的本质联系

以平行四边形概念教学为例，学生很容易忘记概念的先后推导关系，将几个相似的概念弄混，因此，教师在教学过程中就可以引用逻辑推导图来帮助学生建立概念上的清晰认知.如下图所示：

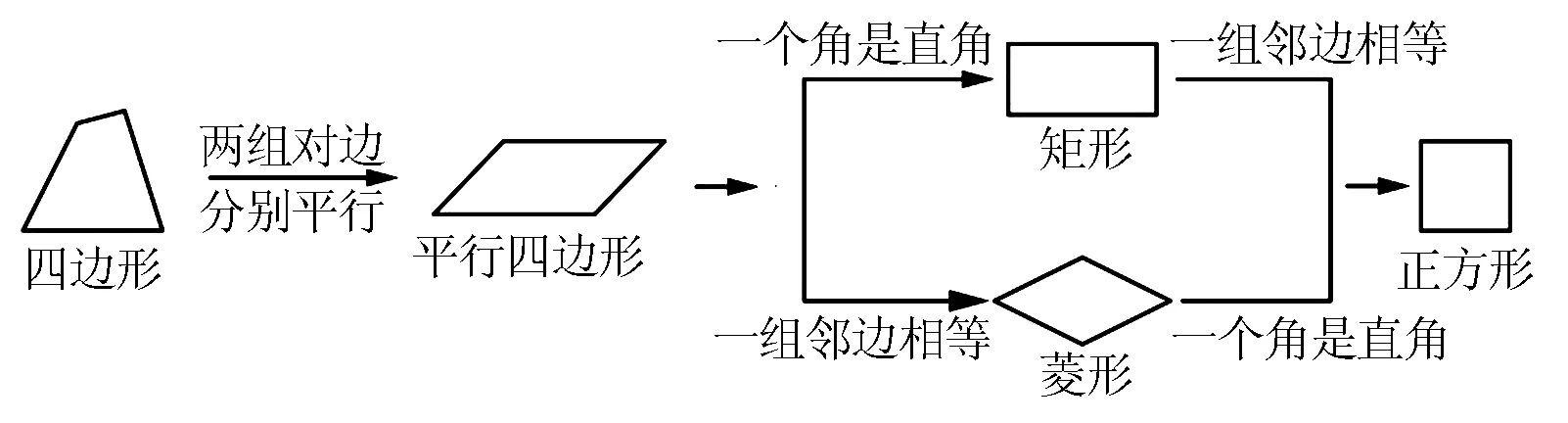
2.明确概念的内涵意义，廓清概念外延

数学概念是在整个人类文明历史发展过程中逐渐形成和发展起来的，富含丰富的内涵以及庞大的外延体系，远非一个简单的数学概念可以解释清楚.因此，教师在日常教学过程中，可以在教学目标的基础之上，适当为学生拓展概念知识教学，延伸数学文化知识，拓宽学生的学习视野，激发学生对于数学探究的欲望.在日常概念教学过程中，教师可以采取给出剖析概念的定义、辨析概念否定例证等环节来达到学生对概念内涵与外延的进一步理解.例如，学生在掌握正数、负数、有理数等概念的教学后，要有意识地引导学生将目前为止已知的数作一个统向性概括：自然数→整数→有理数→实数(内涵减小，外延增大)，初步向学生引入实数的概念，引导学生对所学习的数有一个大体认识.

例如，比较x+4与2x大小.

解若x+4>2x，解得x<4；

若x+4=2x，解得x=4；

若x+4<2x，解得x>4.

从而，当x<4时，x+4>2x;

当x=4时，x+4=2x;

当x>4时，x+4<2x.

分析总结在学生对数有一个大体的印象之后，对于理解类似比较大小的问题就会有一个更加全面的了解.利用分类讨论的思想(或者作差法，本题主要采用分类讨论法)，对x的不同取值做一个讨论，以此探究x+4与2x的整体大小.

3.重视概念应用，在变式训练的过程中强化学生对数学新概念的理解

所谓变式材料，是指概念的肯定例证在无关特征方面的某些变化.因此，在初中概念课教学过程中，科学安排适当的变式训练可以有效达到促进学生进一步理解对于概念的逻辑意义的目的，帮助学生将数学新概念中词义与已有的知识结构之间建立联系，并同时获得对数学知识的整体性理解，深化概念图式结构，真正达到促进学生的迁移性思维训练的目的.

例如，教师在讲解完一元二次方程相关概念之后，引导学生解决以下问题，加深对于一元二次方程重点知识的掌握.

例1已知关于x的一元二次方程4ax2-2ax-3x+2a-6=0的常数项为4，求该方程的一次项系数与二次项系数.

解由题意得2a-6=4，解得a=5.

从而方程的一次项系数为-2a-3=-2×5-3=-13，

二次项系数为4a=4×5=20.

在此基础上，教师可以对该习题进行改编：

例2已知关于x的方程(m2-1)x2-(m+1)x-2m=0.

(1)当m为何值时，此方程为一元一次方程；

(2)当m为何值时，此方程为一元二次方程，并写出此方程的二次项、一次项、常数项系数.

解(1)由题意：m2-1=0且m+1≠0，解得m=1,即当m=1时，该方程为一元一次方程.

(2)由题意知，m2-1≠0，即m≠±1时，该方程为一元二次方程

此时方程的二次项系数为m2-1，一次项系数为-(m+1)，常数项系数为-2m.

分析总结通过将一元一次方程与一元二次方程相关知识放在一起进行解决，通过分类讨论方式求解，有助于学生对方程的相关知识有进一步较为清晰的理解.

概念课教学是奠定学生学习数学“知识大厦”的奠基性工程，是引导学生掌握并理解数学的基础，同时也是形成数学思想、数学语言等的出发点，在初中数学课程体系中占据重要的地位.在概念课教学中，应使学生牢固掌握数学概念相关知识，在已有认知概念基础上，利用学生的生活经验，创设有效的问题情景，帮助学生更好地理解数学概念，同时重视概念的迁移应用，促进学生进一步形成良好的数学思维结构，为将来数学的学习奠定坚实基础.