新的区间值直觉模糊集的熵

杨金鑫 ，赵有金

（1.安徽汽车职业技术学院，安徽 合肥 230601；2.合肥工业大学，安徽 合肥 230039）

1 引 言

L.A.Zadeh[1]于1965 年提出犹豫模糊集概念，Atanassov[2]在犹豫模糊集的基础上扩展到直觉模糊集，直觉模糊集包含了隶属度，非隶属度，犹豫度信息，并提出直觉模糊集熵的做法。1996 年，Burillo[3]提出了直觉模糊熵，对直觉模糊集的模糊程度进行了度量。李香英[4]等研究了区间犹豫模糊熵和相似度之间的关系，并引入区间犹豫模糊加权熵的概念。吴文学[5]提出新的区间直觉犹豫模糊集的距离及相似度。张毛银[6]等通过指数函数加权的方法构造出一种新的区间直觉模糊熵。吴敏[7]等通过ELECTRE-I 和TOPSIS 方法，解决了区间值直觉犹豫模糊多属性决策问题。

2 知识准备

2.1 区间值直觉模糊集

区间值直觉模糊集是由Atanassov 和Gargov 于1986 年提出，它同时包含隶属度和非隶属度，比一般的模糊集更有实际意义。

定义1：假设X是一个论域，则一个区间值直觉模糊集可定义为

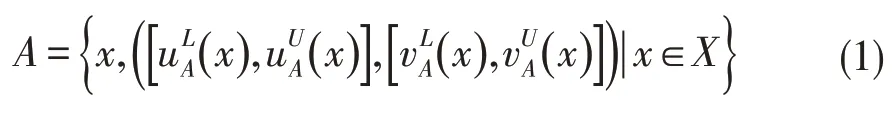
2.2 区间值直觉犹豫模糊集

定义2：假设X是一个非空论域，则一个区间值直觉犹豫模糊集（IVIHFS）可定义为

当X中只包含一个元素，那么便称为一个区间值直觉犹豫模糊数（IVIHFN）。

文献[8]提出区间值直觉犹豫模糊集的犹豫度公式, 而犹豫度公式仅仅只反映了区间值直觉犹豫模糊数中元素个数对决策结果的影响，而未考虑到决策者的分歧程度对决策结果的影响，这可能会导致决策结果与直观认识的不符。为解决这类问题，本文提出一种基于犹豫模糊信息的新型犹豫度，该犹豫度公式包含两个方面：

1.犹豫模糊数中元素的方差，偏差越大，犹豫度越大；

2.犹豫模糊数中元素的个数，个数越多，犹豫度越大。

定义3：设X是一个非空论域，设是 一 个 区间值直觉模糊数（IVIFHN），则的犹豫度可定义为

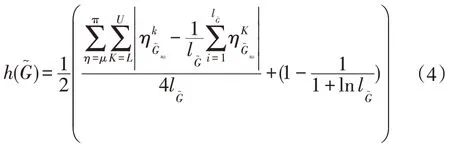
新型犹豫度公式满足如下两个性质：

1.对任意的IVIHFE

2.对任意的IVIHFE

证明：

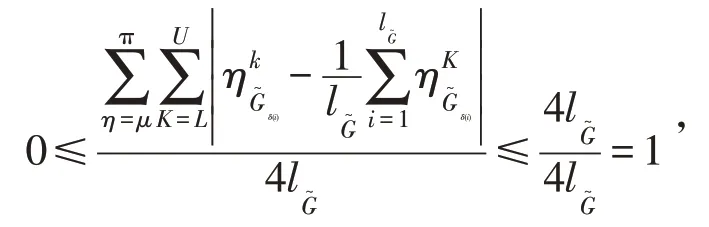
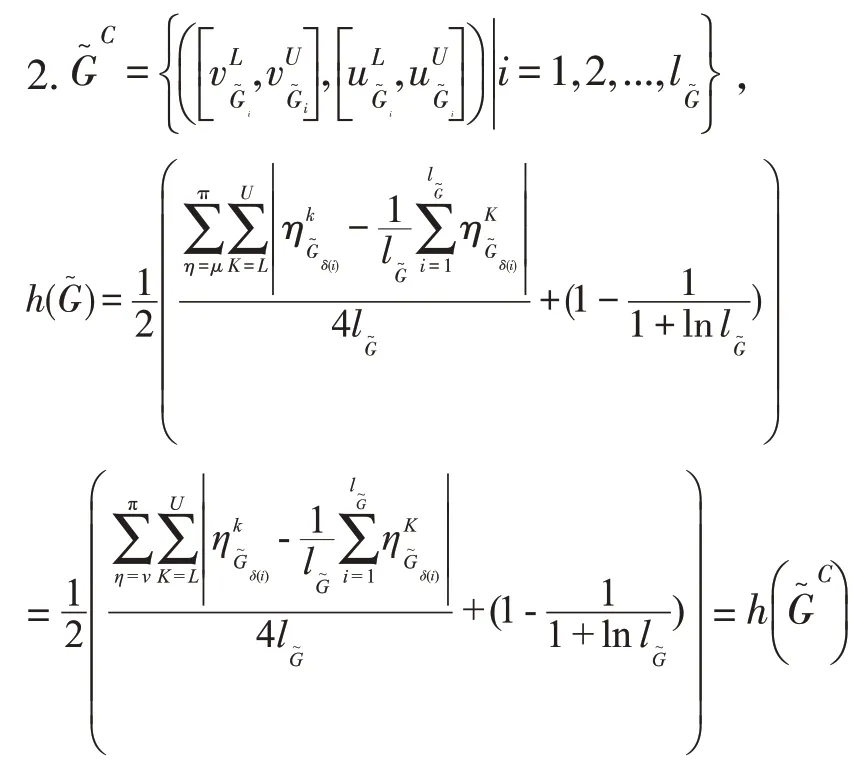
3 区间值直觉犹豫模糊集的熵

熵是对事物不确定性的度量，信息熵的概念源于热力学，由香农（shannon）于1948 年提出。在热力学中，热熵是一种表示分子状态混乱程度的物理量，香农定义信息熵的概念和公式来描述信息不确定的程度。现实中熵的提出和应用是决策的重要工具，是度量一种事物不确定性或模糊性的非常有效的工具。文献[9]提出了IVIHFS 的熵公式，但此熵公式存在一些缺陷，如当隶属度与非隶属度相等时熵都是1，这显然不合理，因为隶属度与非隶属度相等的情况非常多，这种熵公式无法区别隶属度与非隶属度相等时的情况。基于此本文提出新的IVIHFSs熵公式，能有效解决这一缺陷。

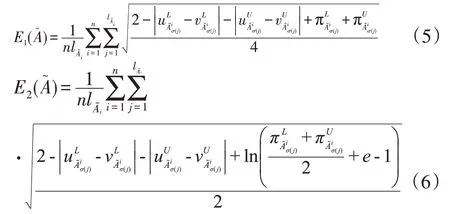
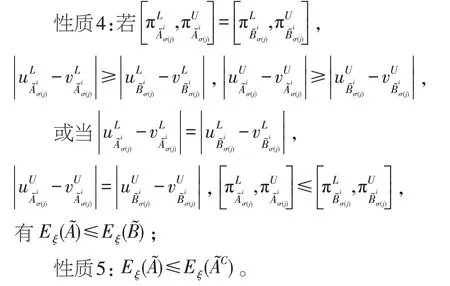
下面分别对两个熵公式的5个性质进行证明。

性质1证明：（必要性）当˜是一个明确集时，则有或

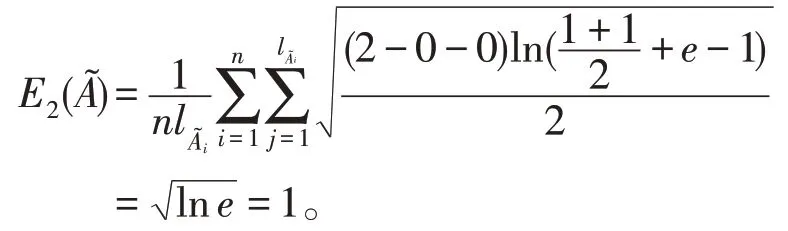
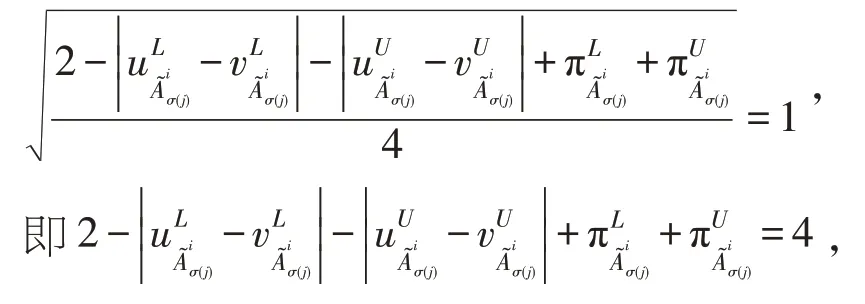
化简可得

将f(x,y,z,w)分别对x,y,z,w求偏导可得

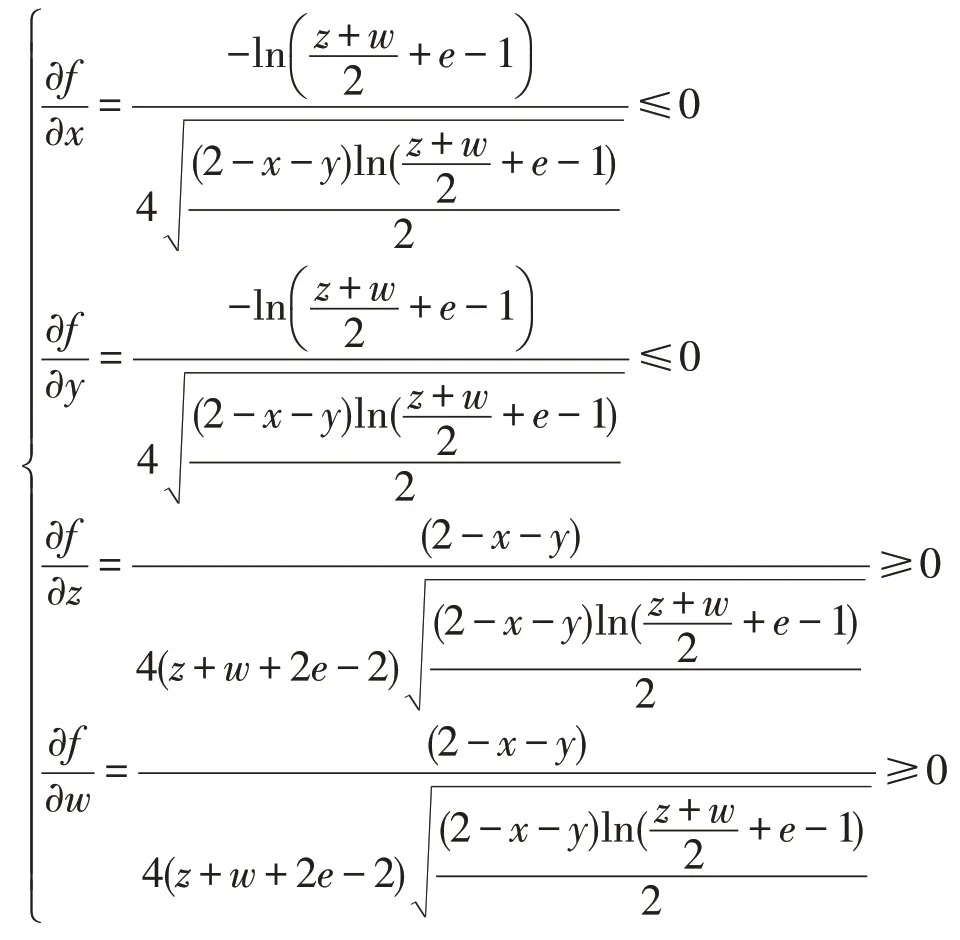
由上式可知，f( )x,y,z,w随着x,y的增大而减小，随着z,w的增大而增大。同理可得随着的增大而减小，随着的 增 大 而 增 大 。 故 当时，最大，为故当时，有

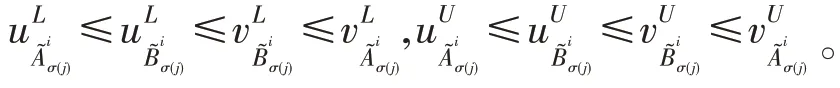
当时，可证得

性质5证明：因为

4 区间值直觉犹豫模糊集距离

因不同的IVIHFSs 的每个Xi∈X的区间值直觉犹豫模糊数的个数以及元素X的个数不一定相等，无法直接做距离，徐泽水[10]提出了当两个集合元素个数不同时，通过添加元素使得两个集合元素个数相等然后进行比较的方法。当决策者风险态度是乐观的，则添加最大值至两者元素个数相等；当决策者风险态度是悲观的，则添加最小值至两者元素个数相等。因为犹豫度的差距也能体现两个IVIHFSs 的差别，本文提出包含两个IVIHFSs 的犹豫度的距离公式。

距离公式包含两个部分：

1.对应IVIHFNs的距离；

2.两个IVIHFSs犹豫度的差异。

定义：设X={x1,x2,...,xn} 是一个非空论域，设是两个 IVIHFSs，其中是 两 个 IVIHFSs，则两个IVIHFSs的距离公式可定义如下：

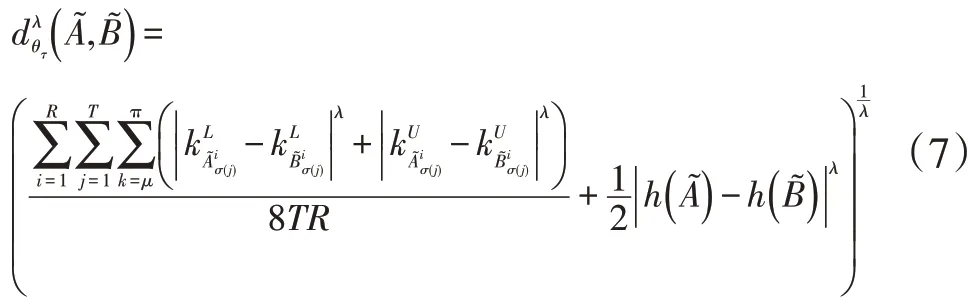
5 实例分析

中国中车常州科技标志实业有限公司（以下简称“公司”）成立于1995 年，隶属于中国中车股份有限公司。自2014年以来，面对来自客户订单增长和新产品开发的压力，公司对由采购部门管理的供应商资源提出了更高的要求。因此，有效评估和选择最佳供应商已成为公司采购部门亟待解决的主要问题。因此，采购部门经过预先评估，确定了3个供应商Xi（i=1,2，3）作为进一步评估的备选方案，每个方案邀请专家进行打分，评分结果作为一个IVIHFS，由于每个专家的偏好不同，故方案数量和决策数量产生不一致。根据IVIHFSs 距离公式，因不同的IVIHFSs 的每个Xi∈X的区间值直觉犹豫模糊数的个数以及元素X的个数不一定相等，无法直接比较，当两个集合元素个数不同时，通过添加元素的方法使得两个集合元素个数相等然后进行比较。当采购部决策者风险态度是乐观的，则添加最大值至两者元素个数相等；当采购部门决策者风险态度是悲观的，则添加最小值至两者元素个数相等。

本文基于决策者风险态度添加元素的方法提出IVIHFSs 距离公式，该距离公式不仅有效简化了计算的复杂度，而且还能度量不同的风险态度对距离产生的影响；同时把犹豫度考虑在内，有效增强了距离测度的科学性和有效性。

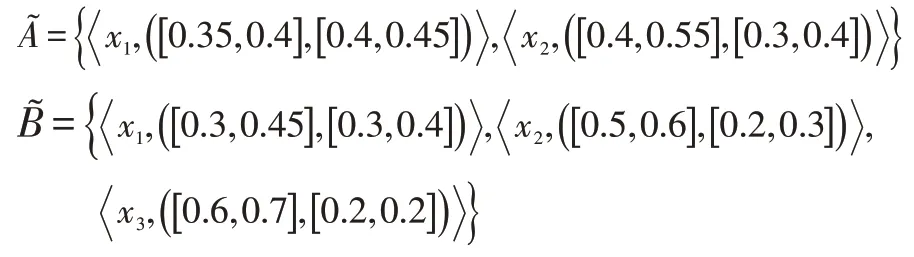
根据本文提出的构造距离的方法，向˜添加一个IVIFN，当决策者风险态度是悲观或者乐观,则可得是两个IVIHFSs。基于文献[8]的熵公式可以得到此熵公式无法区分的熵。但基于本文提出的两个熵公式计算可以得 到因故可知的熵大于˜的熵，有利于决策者做出合理的判断。

6 结 论

基于犹豫模糊信息的新型犹豫度公式，不仅反映了区间值直觉犹豫模糊数中元素个数对决策结果的影响，也考虑到决策者的分歧程度对决策结果的影响，即元素方差和元素个数对犹豫度都有不同程度的影响。基于不确定性和模糊性度量，本文提出了新的IVIHFSs 熵公式，有效区别隶属度和非隶属度相等时的情况。通过添加元素的方法，不仅使得两个集合元素个数相等，可以直接做距离；而且该距离公式包含犹豫度的差异，增强了距离测度的科学性和有效性。