一类具有密度制约的时滞捕食与被捕食系统解的稳定性分析

方辉平

（黄山学院 数学与统计学院，安徽 黄山 245041）

1 引 言

生物数学主要思想是运用数学理论和方法研究生态学中生物种群之间的关系和数量变化, 生态系统种群动力学的稳定性是人们关注的热点问题，文献[1]研究了具有IV 类功能反应函数的捕食与被捕食系统解的情况。而滞后效应是生态系统中普遍存在的，是指系统当前的状态依赖于过去某一个时间的状态，能更加准确地描述客观现象，因此考虑时滞因素对系统的影响，具有很强的理论和实际意义，近些年研究具有时滞项的捕食与被捕食模型越来越多[2-5]。

Freedom和Yao在1983年提出了著名的经典模型

这里c,s,和m均为正常数，其中 0 ＜m≤1，x(t)和y(t)分别表示t时刻被捕食者和捕食者的数量。Freedom和Yao对该模型进行了比较系统的分析，提出了在孕育期种群间相互干扰和时滞对种群的影响。由于种群是相互干扰，因此捕食者在捕获食饵后，需要一定的时间才能转化繁殖下一代的数量。然而，年幼的捕食者需要一定的生长时间才能具有捕食能力。为了更加准确描述两种群之间的增长关系，因此本文考虑两个种群对对方种群数量变化均具有时滞效应的模型。

由于双时滞会给系统带来丰富的动力学行为，也可能使得解及其稳定性发生根本性变化，因此本文主要研究具有相同时滞的捕食与被捕食模型。

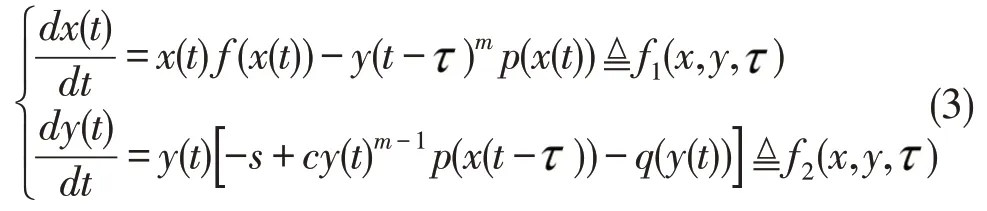
对于模型（3）,假设

1.食饵初始量为正的，受环境影响具有密度制约，即f(0)＞0,f′(x)≤0 ，则存在一个常数K＞0 使得(x-K)f(x)＜0，该常数称为环境最大容纳量；

2.单个捕食者的捕获数随着食饵的增加而增加，即p(0)=0,p′(x)＞0 ；随着捕食者数量的增加，相互挤占空间和竞争捕食越激烈，增长率会降低，即q(0)=0,q′(y)≥ 0 。

2 基本知识

2.1 线性近似系统及其特征方程

通过计算得到系统（4）的特征方程为

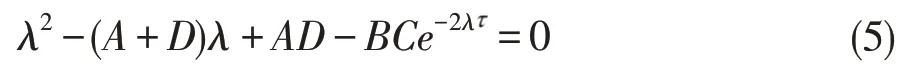
假设该特征方程有纯虚根λ=iω，代入得到

得到关于ω的四次方程

2.2 零解稳定性判定理论

一阶常系数线性微分方程组和二阶常微分方程可以相互转化，因此零解的稳定性保持一致。本文利用Y.Kuang的研究理论分析模型（3）的稳定性。

引理1[6]对于二阶时滞微分方程

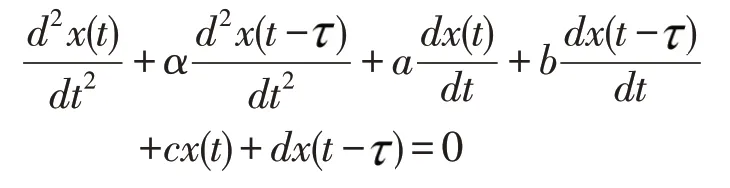
的特征方程是

假设 |α|＜1,c+d≠0,a2+b2+(d-αc)2≠0 ，那么特征方程具有正虚部的不同虚根的个数只可能为0，1，2。

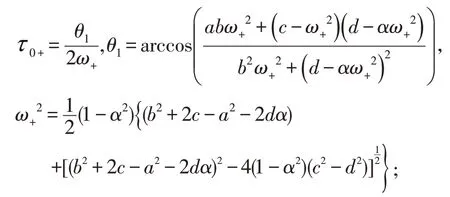
3 主要结果

定理1：假设|AD|＞-BC，则

1.如果AD＜BC＜ 0,对任意的≥0，E(x*,y*)不稳定；

2.如果AD＞ -BC＞0,对任意的≥0 ，E(x*,y*)渐近稳定。

证明：此时（7）式右端小于零，故ω无解。假设TrJ=A+D,DetJ=AD-BC，当=0 时，特征方程（5）化为

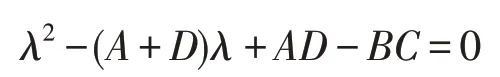
1.AD＜BC＜0 ，则DetJ＜0 ，故 当=0 时 ，E(x*,y*)是不稳定的，由引理1即得当＞0 时，E(x*,y*)也不稳定；

2.如果AD＞-BC＞0,因为D＜0 ，所以A＜0 ，故TrJ＜0,DetJ＞0 ，则E(x*,y*)渐近稳定，所以当＞0时，E(x*,y*)也渐近稳定。

定理2：假设|AD|＜-BC，则

1.如果A+D＞ 0,对任意的≥0，E(x*,y*)不稳定；

2.如果A+D＜0,并且AD＜BC，对任意的≥0，E(x*,y*)不稳定；如果A+D＜0,并且AD＞BC，对任意的0 ≤＜0+，E(x*,y*)渐近稳定；对任意的＞0+，E(x*,y*)不稳定；

3.如果A+D=0,对任意的≥0，E(x*,y*)不稳定。

证明：此时（7）式只有ω2+＞0 ，即λ只有一个虚根的虚部为正数ω+。

2.如果A+D＜0 ，

若DetJ=AD-BC＜0 ，对任意的≥0，E(x*,y*)不稳定。

若DetJ=AD-BC＞0 ，因TrJ=A+D＜0 ，所以当=0 时，E(x*,y*)渐近稳定，则由引理得当0 ≤＜0+时，E(x*,y*)渐近稳定；当＞0+时，E(x*,y*)不稳定。

3.如果A+D=0,

若AD＞BC，则DetJ＜0 ，对 任 意 的≥0 ，E(x*,y*)不稳定；

若AD＞BC，则ω2±=AD-BC＞0 对 任意的≥0 ，此 时 Reλ=0 。 而即当＞0时，λ的实部是正的，所以E(x*,y*)不稳定。

定理3：假设|AD|=-BC，则

1.若AD=-BC，当＞0 时，E(x*,y*)是稳定的。

2.若AD=BC，记则当＞*时，E(x*,y*)是不稳定的。

2.记特征方程（5）的左边为L（λ,）=λ2-（A+D）λ+AD-BCe-2λ，则L（0,）=AD-BC=0，

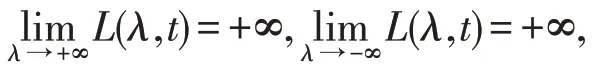
故分别存在一个正数和负数M1,M2，使得当λ＞M1和λ＜M2时，有L（λ,）＞0 成立。

当λ∈(0,δ1())时，L(λ,)＜0。由零点定理得至少存在一个λ*∈(δ1(),M1)，使得L(λ*,)=0，意味着特征方程（5）至少有一个正实根，则E(x*,y*)不稳定。

4 小 结

泛函微分方程理论在捕食与被捕食系统研究中的应用非常广泛，特别是时滞参数的变化对系统的稳定性有很大的影响，利用解析法是研究零解一种非常重要的方法，但仅仅利用特征方程的根去分析有其局限性。例如定理3 第二种情形，当＜*时，很难判定特征方程存在正实部的根或者全部根都具有负实部，因此零解的稳定性难以判定。此外可以利用中心流行定理、几何理论等成果研究周期解的存在性和稳定性、Hopf分支等问题。