一类联图的性质和标号研究
严谦泰
(安阳师范学院 数学与统计学院,河南 安阳 455000)
1 研究背景
优美图由于其有趣性及较好的应用价值和研究前景,研究十分活跃。最近十几年来,国内外取得不少优美图的研究成果[1],它们也被用于许多领域。优美图的研究始于1963年Ringel的一个猜想[2],1972年Golomb明确给出了优美图的定义[3]。之后,Gallian又提出了每棵树都是奇优美的[4],开始了奇优美图的研究。但由于缺少系统和有力的工具,至今只能对一些特殊图类研究其奇优美性[5]。图的强协调标号问题是图论中的一个十分有趣的研究课题,自1982年Frank引入图的强协调标号[6],已有许多这方面的结果[7]。但对于积图讨论以上两种标号的结果很少。
定义1[2]对于简单图G=
定义2[8]设G=
定义3[2]设G=
定义4[2]在图G的每个顶点上都粘接1条边所得的图称为G的冠,记为I(G)。

2 主要结论
引理1图G可嵌入球面S当且仅当G可嵌入平面π。
引理2设G是p(p≥3)阶简单平面图,则G是极大平面图当且仅当|E(G)|=3p-6。

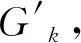
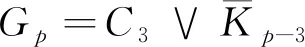
证明根据图的冠的定义及定理1可知,结论成立。
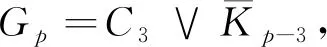
证明显然|E(Gp)|=3p-6,|V(Gp)|=p
建立映射f:V(Gp)→{0,1,2,…,3p-6}
f(v1)=0,f(v2)=2p-4,f(v3)=3p-6;
f(ui)=i,i=1,2,…,p-3
下证f是Gp的优美标号。由上述标号可知f满足:
1)显然,对任意的u,v∈V,若u≠v,则f(u)≠f(v);
2)显然,max{f(v)|f∈V}=|E|=3p-6;
3)令g(e)=|f(u)-f(v)|,e=uv,下证{f(e)|e∈E}={1,2,…,|E|}。由标号f有:
{f(v1ui)=i,i=1,2,…,p-3}={1,2,…,p-3};
f(v2v3)=p-2;
{f(v2ui)=p-2+(p-2-i)=2p-4-i,i=1,2,…,p-3}={p-1,p-2,…,2p-5};
f(v1v2)=2p-4;
{f(v3ui)=2p-4+(p-2-i)=3p-6-i,i=1,2,…,p-3}={2p-3,2p-2,…,3p-5};
f(v1v3)=3p-6=|E|
故{g(e)|e∈E}={1,2,…,|E|}。综上可知f是Gp的优美标号,所以Gp是优美图。
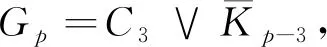
证明由|V(Gp)|=p,|E(Gp)|=3p-6可知,I(Gp)中有2p个顶点,4p-6条边。设I(Gp)中与vi相邻的悬挂点为wi,与uj相邻的悬挂点为tj,i=1,2,3;j=1,2,…,p-3。建立映射f:V(I(Gp))→{0,1,2,…,4p-6}如下:
f(v1)=0,f(v2)=2p-4,f(v3)=4p-6;
f(w1)=2p-3,f(w2)=p-2,f(w3)=2p-5;
f(ui)=i,i=1,2,…,p-3;
f(ti)=2p+1+2(i-1),i=1,2,…,p-3
同样可验证f是I(Gp)的一个优美标号,从而I(Gp)是优美图。
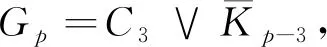
证明建立映射f:V(Gp)→{0,1,2,…,3p-6}如下:
f(v1)=0,f(v2)=1,f(v3)=2;
f(ui)=3i+1,i=1,2,…,p-3
下证f是Gp的强协调标号。
1) 显然f是单射;
2)下证对∀uv∈E(G),令f(uv)=f(u)+f(v),有{f(uv)∣uv∈E(G)}={1,2,…,|E|}。由上述标号可知f有:
f(v1v2)=1,f(v1v3)=2,f(v2v3)=3;
{f(v1ui)=3i+1,i=1,2,…,p-3}={4,7,…,3p-8};
{f(v2ui)=3i+2,i=1,2,…,p-3}={5,8,…,3p-7};
{f(v3ui)=3i+3,i=1,2,…,p-3}={6,9,…,3p-6}
因此有{f(uv)∣uv∈E(G)}={1,2,…,|E|}。综上可知f是Gp的强协调标号,所以Gp是强协调图。
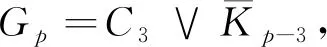
证明建立f:V(I(GP))→{0,1,2,…,4p-6}映射如下:
f(v1)=0,f(v2)=1,f(v3)=2;
f(w1)=3p-4,f(w2)=3p-6,f(w3)=4p-8;
f(ui)=3i+1,i=1,2,…,p-3;
f(ti)=5+4(p-3-i),i=1,2,…,p-3
同样可验证f是I(Gp)的一个强协调标号,从而I(Gp)是强协调图。

