一种基于正则化方法的非负矩阵分解算法研究与应用

李小珍

(安徽国防科技职业学院，安徽 六安 237001)

0 引言

非负矩阵分解(NMF)是由学者Lee和Seung首次提出的矩阵分析方法，随着信息化技术的快速发展，矩阵分解在大数据处理和模式识别中发挥着越来越重要的作用[1]。传统的矩阵分解工具，结果中普遍含有负数，这为实际应用带来了一定的难度。与此不同的是，非负矩阵分解的所有结果均为非负值，对象的物理表达更加自然，具有更加广阔的应用前景。但是传统非负矩阵分解方法无法同时考虑数据样本特征信息和数据固有几何结构，在一定程度上影响了数据的聚类结果。本文将图正则化方法和半监督学习思想深度结合起来，提出新的非负矩阵分解算法。该方法充分考虑样本的类别信息和数据空间的几何流行结构信息的有效性，并以图像聚类为例，选择ORL数据集进行算法验证[2]。

1 图像分类与模式识别

图像数据的维度较高，直接影响了图像分类的准确性和运算效率，所以图像分类的第一步就是图像降维。降维能够去掉冗余的维数，将有用的维数保留下来，实现高维数据低秩逼近。图1所示为图像分类的基本框架，首先通过图像降维处理获得图的特征值、特征向量，然后将其输入分类器或者支持向量机，以此实现图像分类。

图1 图像分类的框架

2 非负矩阵分解

2.1 非负矩阵分解的基本概念

对非负矩阵X∈Rm×n来说，矩阵分解的目标就是为了得到两个非负矩阵W∈Rm×r和H∈Rr×n，使得X≈WH，其中r=min(m,n)。X≈WH的求解可以近似看做是求最优解的问题。常用的非负矩阵分解的目标函数有基于欧式距离和基于K-L散度两类。

基于欧式距离的目标函数可以表示为：

(1)

基于K-L散度的目标函数可以表示为：

-Xij+(WH)ij)2

(2)

在统计独立性方面，K-L散度具有突出优势。K-L散度是X和WHT差异的非对称性度量。当X=WHT，K-L散度函数最小值为0。如果单独分析矩阵W和H，那么上文提到的目标函数为凸函数；如果同时考虑矩阵W和H，那么目标函数不是凸函数。非负矩阵分解之后的矩阵W和H具有稀疏性，可以有效的降低数据冗余。但是，这种方法带来的稀疏性不够明显，很多情况下无法满足应用要求，所以需要在目标函数中增加稀疏限制项。非负矩阵分解算法及其常见的改进算法中，矩阵W和H的初始值都是随机选择的，这些随机值均为非负值。如果实际问题相关信息不明确，那么W和H的初始值无法确定，只能随机选择。非负矩阵分解算法类似于约束优化问题，执行问题的步骤复杂繁多，选择最优分解也带来了很大的时间消耗，无法满足实践应用需要[3]。

2.2 迭代规则及算法收敛性

利用乘性迭代算法更新W，利用交替迭代算法更新H，不仅能够提升收敛速度，也能够降低计算难度。

Lee和Seung[4]提出一种乘法更新算法，将(1)更新为：

(3)

式(2)的更新规则可以表示为：

(4)

其中1≤i≤m,1≤j≤n,1≤k≤r，转置矩阵表示为T，基矩阵表示为W，其中的列称为基向量，系数矩阵表示为H。矩阵W和H的初始值随机，在运算过程中不断更新矩阵W和H的值，直到矩阵的变化足够小，获得矩阵分解结果。为了确保更新过程中不因为分母为零而导致异常，在分母上要添加一个足够小的正数。

欧式距离函数(1)单调递减，如果W和H是函数的稳定点，那么函数值不再继续变化。

K-L散度函数(2)单调递减，如果W和H是函数的稳定点，那么函数值不再继续变化。

在讨论非负矩阵分解算法的收敛性时，引入了辅助函数[5]来分析，并导出迭代规则。

定义G(k,k′)为F(k)的辅助函数，并且满足式：

G(k,kt)≥F(k),G(k,k)=F(k)

(5)

2.3 图正则非负矩阵分解算法

采用图正则化方法的非负矩阵分解算法，就是在进行矩阵分解时，明确低维度空间样本数据的基本几何结构。假设存在两个数据点，分别表示为xi和xj，它们在原数据空间是邻近的关系，那么在新的基矩阵下其对应的vi和vj也是邻近关系。

假设G是由原始数据点组成的图，权重矩阵用Sij来表示，xi的p个邻近数据点由Np(xi)表示，那么：

(6)

式(7)为图正则化非负矩阵分解算法的最小化目标函数：

(7)

迭代更新规则表示为：

(8)

3 基于图正则化和稀疏约束的半监督非负矩阵分解

在特征提取方面，非负矩阵分解算法只能在数据原始空间展开，在变形空间无法实现。本文提出在非负矩阵分解算法基础上，对基矩阵进行稀疏约束，引入拉普拉斯正则化约束，最终有效减少运算环节和节约存储空间，提升非负矩阵分解的效率。

本文提出的新的最小化目标函数可以表示为：

(9)

上式中，标签约束矩阵可以表示为A，拉普拉斯矩阵表示为L，正则化参数表示为λ，稀疏系数表示为β，β∈(0,1)。‖g‖F表示的是F范数。按照迭代法和最速下降法的原则，式(9)的迭代规则可以表示为：

=Tr(XXT)-2Tr(SAZWT)+Tr(WZTATAZWT)

(10)

φ和φ表示的是约束Wik≥0,Zjk≥0对应的拉格朗日乘子，那么可以将拉格朗日函数表示为：

L1=OF+Tr(φWT)+Tr(φZT)

(11)

求解W和Z的偏导数，令它们的值为零，那么：

(12)

利用KKT条件，可以将迭代规则确定为：

(13)

根据上述分析，目标函数和Z中任意元素Zij相关的部分可以表示为Fij，那么：

(14)

此处假设F′表示的是Z的一阶微分，那么Fij的辅助函数可以表示为：

(15)

证明G(z,z)=Fij，按照辅助函数的定义，则需要证明G(z,zt)≥Fij(z)。Fij(z)的泰勒展开可以表示为：

(16)

相较于辅助函数，可以将G(z,zt)≥Fij(z)等价表示为：

≥(AAT)ii(WTW)jj+λ(ATLA)ii

(17)

已知

≥zt(ATA)(WTW)

(18)

且

≥λ(AT(D-U))zt=λ(ATLA)zt

(19)

得证。

4 实验验证

在Windows10环境下，利用Matlab R2012b进行算法的验证。此次验证基于英国剑桥Olivetti实验室提出的人脸图像数据库ORL展开。所有图像的尺寸都是92×112。ORL数据集共有400张图片，维度为1024，共40个类别。

首先从ORL数据集的各个样本类中选取包含有标记信息的样本，从其中随机的选择K类样本开展聚类分析，本文选定的实验次数为20次。

图2 ORL数据库的图像举例

算法的聚类性能采用聚类准确率(AC)的指标来分析，即数据集中正确分类的样本的占比。如果样本的数据量为n，ri表示给定的正确样本类别信息，li表示聚类后的样本信息。则

(20)

上式中，δ(x,y)表示二值函数。如果x=y，那么二值函数值为1；如果x≠y，那么值为0。map(li)表示映射函数，是li和数据集中其他类别的样本之间的映射关系。

互信息表示聚类样本之间存在的相关性，即MI。假设存在两个聚类样本集，分别表示为C和C′，则：

MI(C,C′)

(21)

将其归一化之后，可以表示为：

(22)

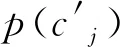
此处正则项参数λ取值为100，稀疏系数β的取值为0.3。

图3 ORL数据集的收敛曲线及聚类准确率

图3所示为利用ORL数据集实验后的收敛曲线，实验结果表明利用该方法迭代50次左右就能够满足收敛要求。采用几种不同的非负矩阵分解算法，对每个随机的k值运行20次后，最终的聚类结果表明该算法在图像聚类方面效率良好。

5 结语

总体来看，利用本文提出的新的非负矩阵分解算法，降维之后的图像聚类效果远好于一般的非负矩阵分解算法，并且稳定性能保持在良好的范围内，该算法在图像分类中有良好的应用效果。