基于流固热耦合分析的螺旋槽泵出型动压密封端面结构参数优化*

李双喜，廖浩然，李世聪，刘兴华

(北京化工大学 机电工程学院，北京 100029)

0 引 言

在化工、航空航天等领域中，常常使用氦气等惰性气体多级密封两种气体燃料，惰性气体会向气体燃料侧泄漏造成污染，泄漏量过大将使得燃料纯度过低造成严重后果。螺旋槽泵出型动压密封与传统干气密封不同，其于高压内径侧开动压槽，能在微小泄漏率的情况下，保证高压介质泵出，避免高压介质污染。

实际工况中，由于结构、流体、温度都会对密封端面状态造成影响，在端面参数选择不当的情况下，端面容易发生摩擦、磨损进而引起密封失效。

耦合分析是一种综合考虑多种方面影响的研究方法。胡琼等人[1]建立了三维传热模型，研究了主轴转速等对热-力耦合变形的影响；罗显等人[2]耦合端面波度、锥度变形计算了流体模型，研究了槽型对非接触密封性能的影响；黄伟峰等人[3]耦合多物理场建立了流固热耦合仿真模型，研究了八字槽泵出型密封性能，揭示了温升和变形对泵送的削弱效应；王计辉等人[4]建立了热力耦合模型分析摩擦副摩擦特性；白瑜光等人[5]利用高斯-赛德尔分块迭代耦合方法，分析了密封结构内部空腔流动传热以及外部传热对密封的影响；陈汇龙等人[6]对密封端面进行了流固热耦合分析，得到了内外径侧流体膜厚度变化数据为16%。国外学者根据微间隙流体流动特性[7-8]、两相流颗粒分散机理[9]以及螺旋槽端面润滑状态[10]建立了微间隙流场模型。

槽型是影响干气密封性能的重要因素。现有学者对人字槽[11]、螺旋槽[12-14]、T型槽[15]、双螺旋槽[16-18]、树形槽[19]等端面槽型的干气密封性能进行了分析，得到了各结构参数与工况对密封性能的影响关系。

现有研究多为总结流固热耦合方法以及关于端面槽型的研究[20]，缺少考虑热以及端面变形的泵出型动压密封流体的分析。

本文将提出螺旋槽泵出型动压密封结构，基于气相流体控制方程，采用流固热耦合分析方法，研究各螺旋槽结构参数对密封性能的影响；揭示螺旋角、槽数、槽堰比、槽坝比和槽深，对开启力、泄漏量、摩擦功耗和气膜刚度等密封性能的影响趋势。

1 结构工作原理

螺旋槽泵出型动压密封结构如图1所示。

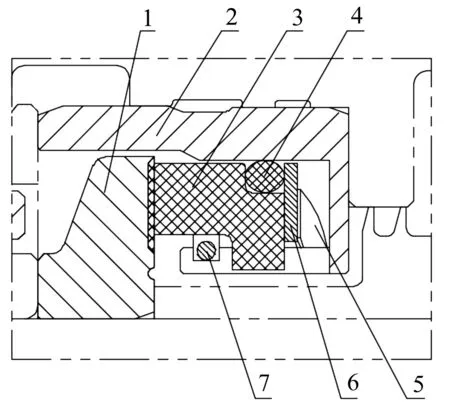
图1 螺旋槽泵出型动压密封结构1-动环；2-静环座；3-静环；4-O形圈；5-波形弹簧；6-弹簧垫；7-卡圈

密封主要由动环和静环组件两部分组成，图1中右侧为高压介质。动环上刻有微米级的动压槽。静环组件是由静环、静环座、O形圈、波形弹簧、弹簧垫和卡圈组成。动环与静环的接触面为主要泄漏面，O形圈与弹簧座的接触面为次要泄漏面。在静止时，静环受到弹簧的作用与动环紧密贴合密封两侧气体；在高速旋转时，高压气体进入螺旋槽，随着流道变窄，在槽内产生动压效果。当动压效果足够大时，密封动静环被推开，端面间会形成一层具有一定刚度的微米级气膜，阻止另一侧流体流入，达到密封的效果。动压泵送方向、离心力以及流体剪切力方向都是由高压侧指向低压侧，因此将此类密封称为泵出型密封。

工作时端面间产生的动压效果与端面结构参数相关，本文采用恒定膜厚的分析方法，研究结构参数与密封性能之间的关系。

螺旋槽泵出型动压密封端面流场分析结构参数如表1所示。

表1 螺旋槽泵出型动压密封端面流场的结构参数

2 分析模型

2.1 气相流体控制模型

描述动压密封端面间流体膜压力分布的基本方程为压力控制方程(Reynolds方程)：

(1)

式中：ρ—气体密度；h—流体膜厚度；p—压力；η—气体粘度；r—径向坐标；θ—角向坐标；ω—转速。

对式(1)求解方法主要是基于伽辽金法的变分方程，对压力控制方程进行离散，利用有限元方法，对计算域内总方程进行求解，求得流体膜离散后的压力值；根据压力值进一步计算得到动压密封的工作膜厚、泄漏量、流体膜刚度及摩擦扭矩等动压密封性能参数。

2.1.1 假设条件

针对动压密封端面流体膜的实际特点，需要对密封端面间流体膜做如下合理的基本假设：

(1)根据Reynolds准数计算公式得到密封端面间流体的Reynolds数大约为200，故流体在动静环端面内流动为层流；

(2)端面流体膜很薄，工作膜厚方向和端面方向的尺寸相差几千倍，可假设流体密度和压力沿工作膜厚方向不变；

(3)忽略流体的惯性力和流体的体积力；

(4)假设流体与动静环接触不产生相对滑动；

(5)假设速度梯度只考虑∂u/∂z和∂v/∂z；

(6)假设流体膜内流体的流动过程中是温度、粘度恒定。

2.1.2 边界条件

压力控制方程求解需要同时满足如下边界条件：

(1)密封的外径侧为介质端，为压力入口，内径侧为大气端，为压力出口。

r=ri时，p=pi；

r=ro时，p=po。

(2)密封的周向两侧的壁面为周期性边界条件：

(2)

2.1.3 端面厚度分布方程

压力控制方程需要重点考虑端面结构对端面压力分布的影响，因此，必须引入流体膜厚度方程，即：

h(r,θ)=h0(r,θ)+δghg

(3)

式中：δg—位置因子。

当计算区域位于动压槽时，δg=1；计算区域位于非动压槽区时，δg=0，引入端面厚度分布方程可以解决式(1)的缺陷，并考虑端面结构，以保证计算准确性。

2.2 流固热耦合分析模型

实际运转工况中，端面受到离心力、压力、温度的影响会发生变形，将会引起端面流体膜厚度变化，影响流体膜压分布与密封性能。流固热耦合通过耦合流体、固体、热计算，并设定收敛精度的方法，得到贴近实际的流体膜压分布，计算流体密封性能。由于流体膜压力变化对温度的影响不大，为了方便计算，此处只考虑温度对流体膜单向的影响。

流固热耦合分析流程图如图2所示。

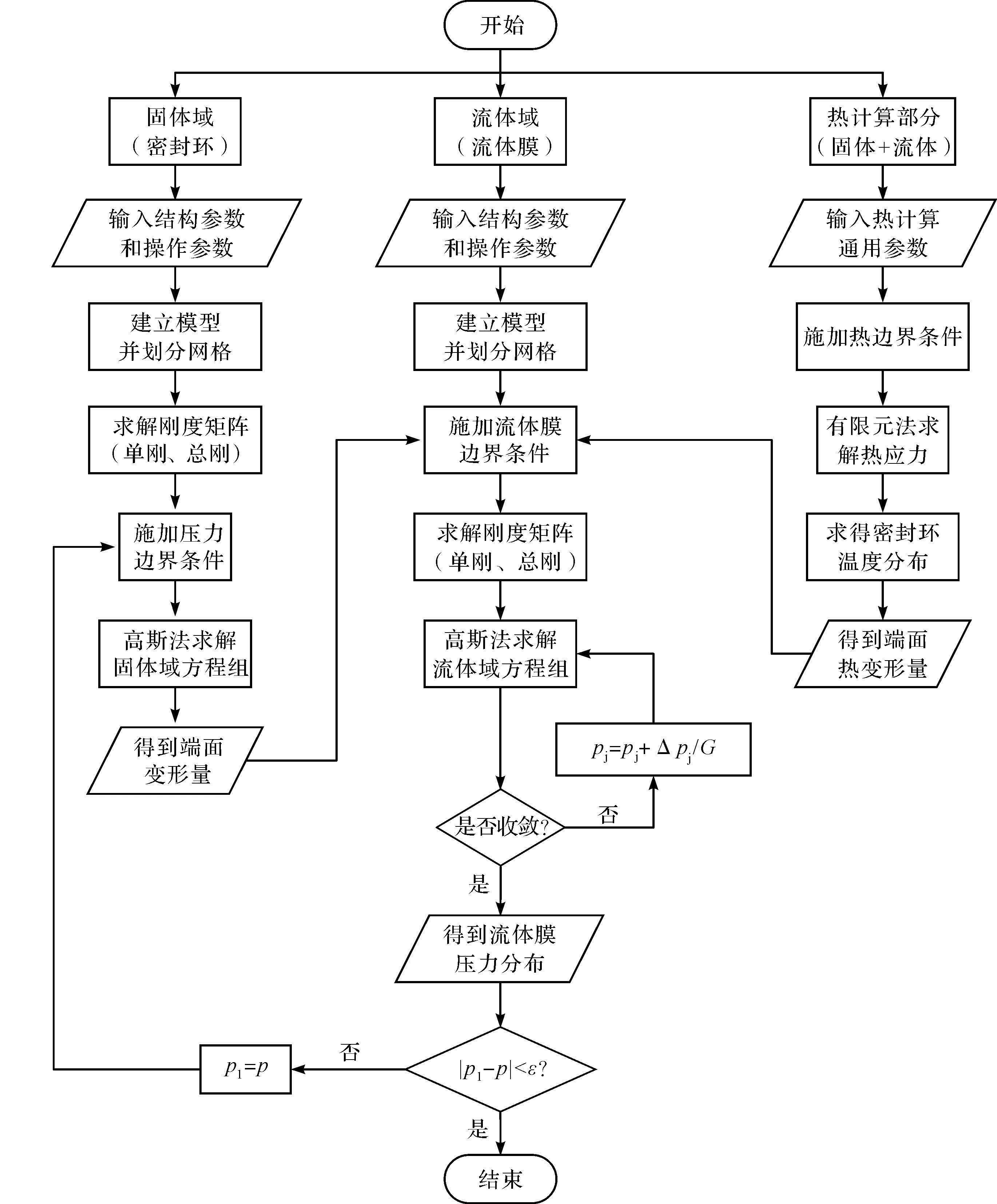
图2 流固热耦合分析流程图

耦合计算具体步骤如下：

(1)根据输入参数划分网格，计算密封环变形分量δij和δid；

(2)修正流体膜膜厚初始厚度，得到流体域计算初始厚度修正值hi(hi=ho+δij+δid)；

(3)通过热计算得到热变形δkj和δkd；

(4)通过流体计算，得到压力分布p1；

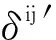
反复进行迭代计算，当压差满足设定精度(ε)时，流体膜压力分布、密封环变形达到稳态。

由分析可知，动静环端面外径侧较高，内径侧较低，这是为收敛间隙，有利于密封的稳定以及泄漏量的减小。由于存在动压槽，局部端面变形发生变化，分析可得动环相对最大变形量在1×10-5mm左右，静环面相对变形量在3×10-5mm，变形量较小。

通过流固热耦流体合膜压分布可知，在工况条件下密封能够产生较好的动压效应。

3 试验及结果分析

本文采用试验的方法，验证密封可行性以及数值分析结果。

运转前后静环端面微观形貌图如图3所示。

图3 运转前后静环端面微观形貌图泛光白点—浸入石墨的金属锑

从图3中可以看出：运转前静环端面平整、无划痕；运转后的端面存在方向为左下角到右上角的规则划痕，这是由于在提升转速过程中低速段动静环端面未开启密封，引起的轻微摩擦。

采用精度为0.1 g的英衡电子称测得运转前后静环质量差为0.0 g，在高转速下几乎无磨损，螺旋槽泵出型动压密封设计可行。

不同压力下，试验与计算泄漏量变化曲线如图4所示。

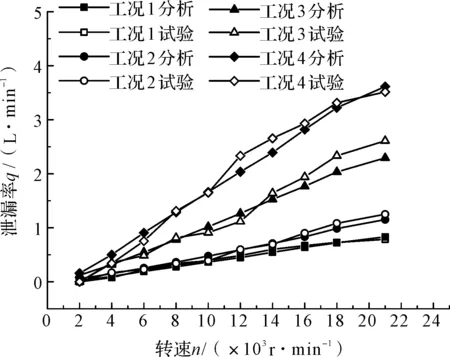
图4 不同压力下试验与计算泄漏量变化曲线

图4中，工况1～工况4分别是在压力为0.05 MPa、0.1 MPa、0.15 MPa、0.2 MPa工况下进行的试验。泄漏量随着转速的增加而增加，压差更大时，泄漏量越大。试验泄漏量与计算泄漏量随转速的变化趋势相同，且计算误差很小。

由此可见，流固热耦合螺旋槽动压密封性能分析计算具有参考意义。

4 结构参数优化分析

螺旋槽动压密封性能主要通过调控螺旋角、槽数、槽堰比、槽坝比和槽深等端面参数来实现。

分析结构参数如表1所示，设定分析外压为0.15 MPa，内压为0 MPa，介质初始温度为20 ℃。研究转速为10 000 r·min-1与20 900 r·min-1两种实际工况转速下的密封性能。优化前恒定膜厚开启力参考值为282.3 N，泄漏率为5.51 mg/s。

4.1 螺旋角

螺旋角对密封性能的影响如图5所示。

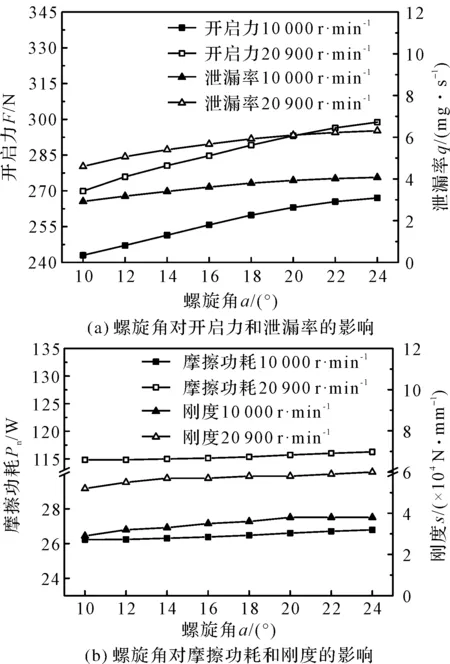
图5 螺旋角对密封性能的影响

由图5可知：开启力随着螺旋角的增加而增加，在螺旋角为15°～20°以后，增加趋势减缓；

泄漏率随着螺旋角的增加而增加，且增加速度逐渐减缓。这是由于在研究范围内，螺旋角的增加使得流体进入螺旋槽的阻力减小，动压效果增强，在22°～24°附近泄漏量、开启力大；

摩擦功耗受螺旋角的影响不大，而高转速下摩擦功耗变化趋势与较低转速存在区别，这是由于摩擦功耗主要与端面状态以及变形相关，而高转速下端面变形相对较大；

气膜刚度随着螺旋角的增加而增加。开启以后，转速不会影响流体进入螺旋槽的过程，不同转速下螺旋角对各密封性能的影响趋势相同。

增大螺旋角有助于提高开启性能，但同时泄漏率增大对密封的正常工作不利。较小的螺旋角会减小开启力，进而需要更大的转速平衡闭合力，密封需要更大的转速才能开启与保证气膜刚度。

因此，综合考虑螺旋角对密封性能的影响，螺旋角取15°～20°较为合理。

4.2 槽数

槽数对密封性能的影响如图6所示。

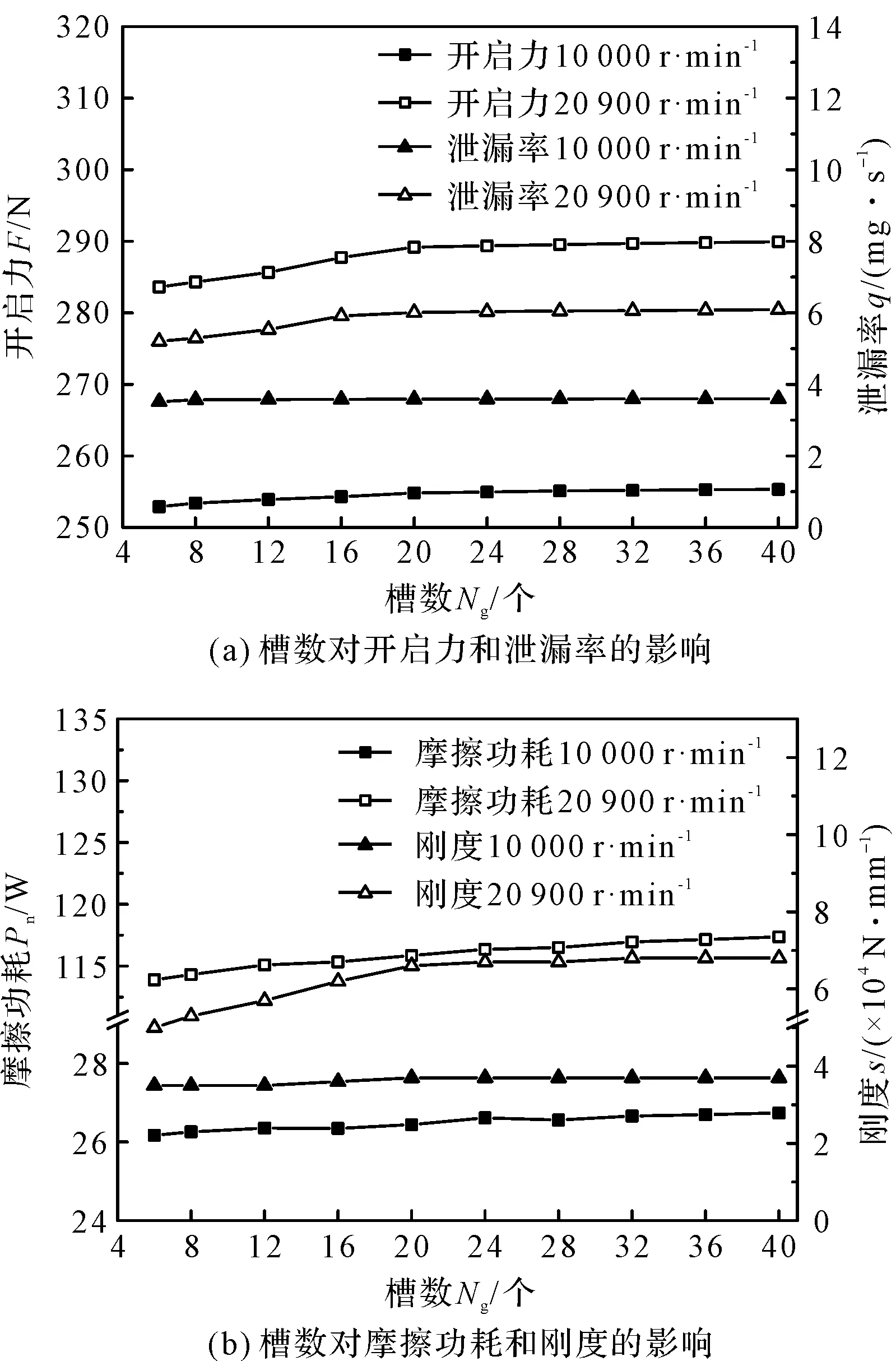
图6 槽数对密封性能的影响

由6可知：开启力随着槽数的增加而增加，最后逐渐稳定；槽数为16个～20个以后开启力达到最大，这是由于槽数较少时，流体进入螺旋槽产生的动压效应不明显。槽数增加，泄漏通道增加，体积泄漏率随槽数的增加而增加，在槽数为16个左右时达到最大。低转速下，由于整体泄漏量较小，其随槽数的变化规律不明显；

摩擦功耗随着槽数的增加而增加，这是由于槽数的增加使得端面状态变差，摩擦生热增加。槽数的增加使得气膜刚度增加，在槽数为16个～20个时增加趋势减缓，之后保持稳定。当槽数超过16个时，开启力、泄漏率、刚度和功耗趋于稳定。

为保证良好的开启力以及较小的泄漏量，槽数取12个～16个较好。

4.3 槽堰比

槽堰比对密封性能的影响如图7所示。

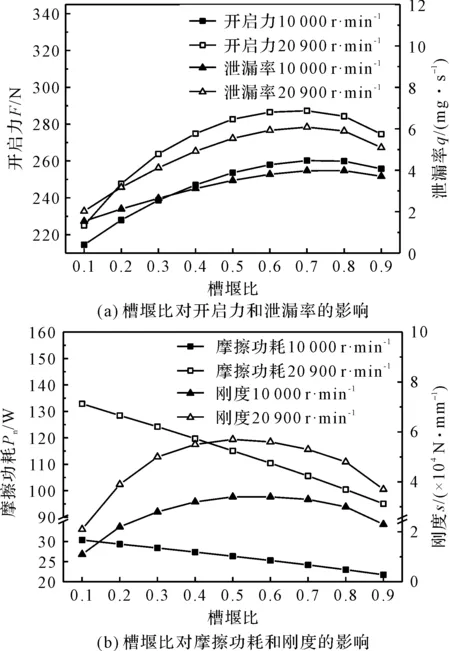
图7 槽堰比对密封性能的影响

由图7可知：开启力和泄漏率在槽堰比为0.6～0.75内有最大值，这是由于较大的槽堰比，流体更容易进入槽区产生动压效应与较大的泄漏量。而当槽堰比过大时，流道过宽，动压效应不明显。槽堰比越大，密封端面间的平均间隙也增大，引起端面间的剪切力减小，功耗减小。在槽堰比为0.5时，槽区与堰区占比相同，膜压分布最为均匀，气膜刚度达到最大，因此刚度的最佳范围是0.4～0.6。

综上所述，槽堰比应取0.5～0.6之间。

4.4 槽坝比

槽坝比对密封性能的影响如图8所示。

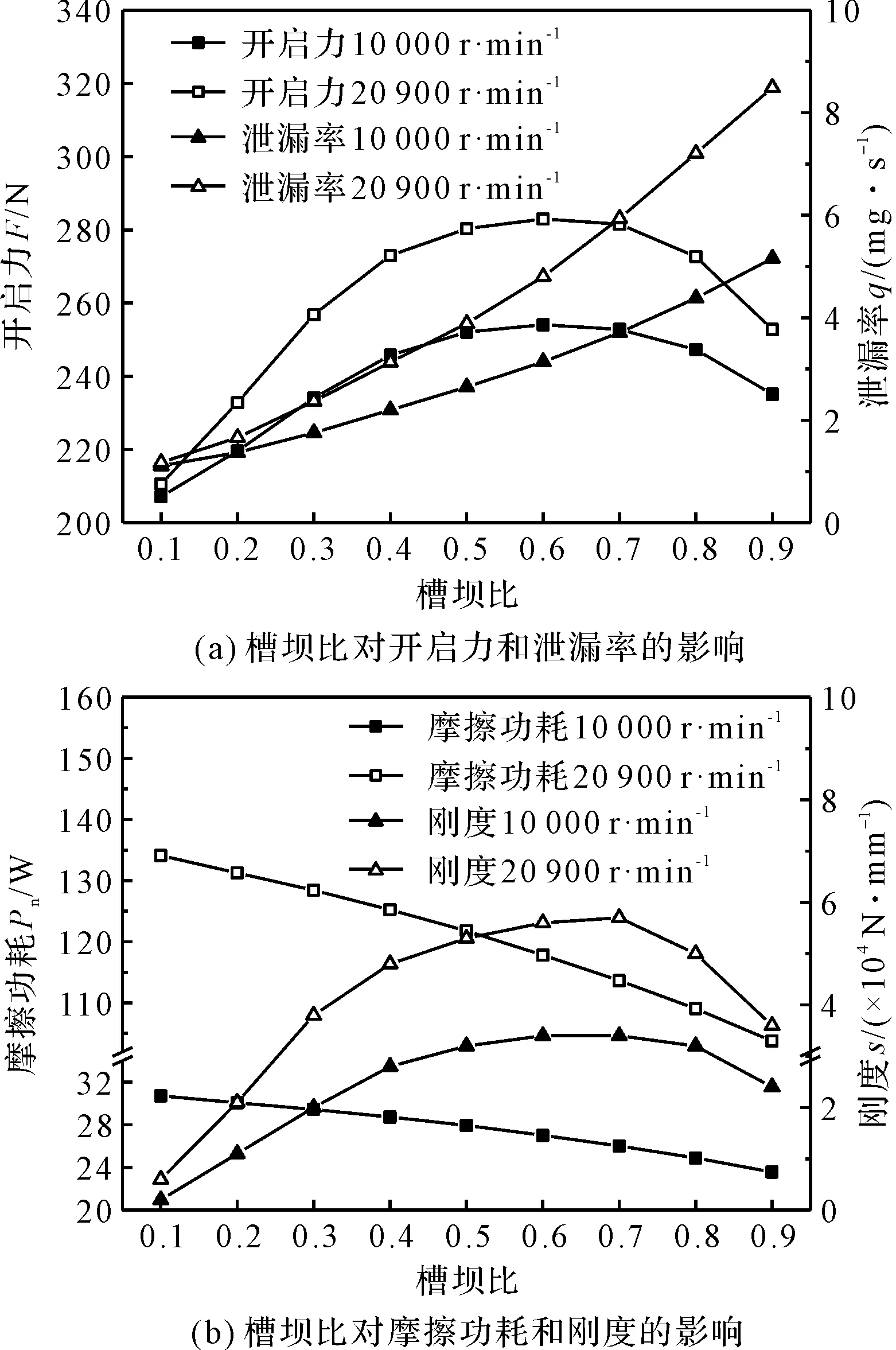
图8 槽坝比对密封性能的影响

由图8可知：开启力随着槽坝比的增加先增加后减小，在槽坝比为0.5～0.7时开启力取得最大值，泄漏量随着槽坝比增加而增加。这是由于小的槽坝比不利于流体进入槽内，大的槽坝比使得坝区减小，流体阻力减小，使得动压效果降低，泄漏量增大，端面接触面积越小，端面状况不确定性减小，因此，摩擦功耗随着槽坝比的增加而减小。

槽坝比增大时，高转速与低转速下泄漏量差别变大，这是由于大槽坝比与端面锥度变形情况下，气体更容易泄漏。气膜刚度在槽坝比过大时，承载能力以及节流能力减小，刚度在0.55～0.75之间取得最大。

综上所述，槽坝比在0.65～0.75之间时，综合密封性能最佳。

4.5 槽深

槽深对密封性能的影响如图9所示。

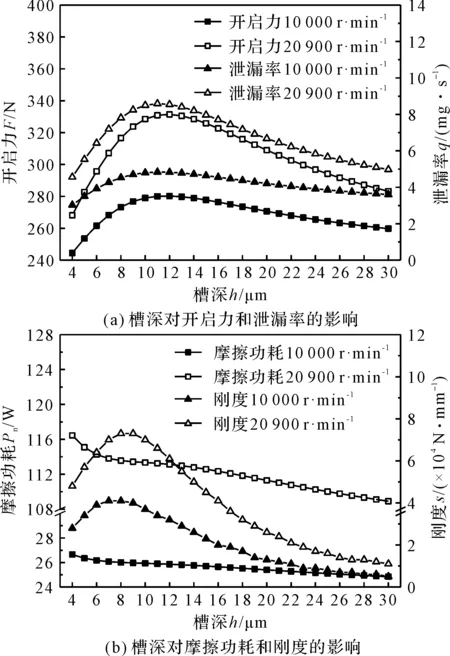
图9 槽深对密封性能的影响

由图9可知：当槽深小于12 μm时，开启力和泄漏率随槽深的增加而快速增加，但当槽深超过12 μm时，开启力和泄漏率都缓慢下降。这是由于槽深太大导致流体进出槽区阻力更大，动压效果降低。而槽区局部高压减小，槽区与外侧压差减小，泄漏量减小；

功耗随槽深的增加而减小。槽深在5 μm～10 μm时，气膜能够产生一定的动压效果，承载能力较好，同时气膜厚度变化相对较小，刚度达到最大。

综上所述，槽深在7 μm～10μm左右时具有较好的开启力、泄漏率和刚度。

5 结束语

采用试验方法，笔者验证了采用流固热耦合分析方法的数值模型，分析了螺旋槽泵出型动压密封结构参数对密封性能的影响。

研究得出的具体结论如下：

(1)试验静环几乎不存在磨损，验证了螺旋槽泵出型动压密封的可行性。对比试验与分析数据，验证了基于流固热耦合分析模型的正确性。该结果可为螺旋槽泵出型动压密封的设计与发展提供理论和试验基础；

(2)开启力和泄漏量随螺旋角和槽数的增加而增加，并逐渐稳定。开启力随着槽堰比、槽坝比和槽深的增加而先增加后减小。泄漏量随着槽坝比的增加而增加，并且趋势加剧，随着槽堰比和槽深的增大而先增大后减小；

(3)摩擦功耗和气膜刚度随着螺旋角和槽数的增加而缓慢增加。摩擦功耗随着槽堰比、槽坝比和槽深的增加而减小。气膜刚度随槽宽比和槽深的增加而先增加后减小；

(4)当螺旋角为15°～20°、槽数为12～16、槽堰比为0.5～0.6，槽坝比为0.65～0.75，槽深为7 μm～10 μm时，开启力和气膜刚度较大，泄漏和摩擦力较小，螺旋槽泵出型动压密封综合性能最好。