基于条纹薄膜的非接触式振动测量和模态分析系统研究*

徐宗煌，钟舜聪，林云粦，刘 峰，陈 曼

(福州大学 机械工程及自动化学院，福建 福州 350108)

0 引 言

声音的频率在20 Hz-20 kHz之间。现阶段的声音测量方式主要有声压测量、声强测量和声功率测量等[1]。其中，最常见的是通过电学麦克风的形式进行声压的测量，其工作原理是通过空气中的振动压力波，将声音信号转化为电信号[2]。

电学麦克风虽然具有较高的灵敏度，但是存在电信号的转换，会受到外界电磁信号的干扰[3-5]。随着光纤传感技术的发展，人类开始利用以光波为载体的光纤麦克风来测量声压[6]，其主要原理是利用声音信号的声压作用改变反射面与光学镜头之间的距离，使得光电探测器上接收到的光强信号发生改变，从而感知声压的大小及变化[7-8]。由于其是光纤结构，具有良好的抗外界磁场信号干扰的性能，然而光纤麦克风对振动膜的要求比较高，不但需要高反射率、制备方便的振动膜，而且容易受到外界环境和光源稳定性的影响，精度不高。此外，其光纤结构装置和解调系统相对比较复杂[9]。

传统的振动测量方法是利用加速度传感器，但是因为传感器有自身的质量，在一定程度上会影响结构模态分析，特别是测量薄壁结构的模态分析时。

因此，笔者提出一种条纹薄膜实现对非接触式的振动测量方法。

1 薄膜振动的理论基础

一般来说，利用麦克风测量声音信号，其主要功能是测量声音的大小和频率，其分别是通过振膜的振幅和振动频率来表现[10-11]。由于振膜起作用的主要是一阶振动模态[12]，这里推导振膜的一阶谐振频率的公式。

1.1 圆形振膜振动理论

假设圆形振膜的边缘被固定在支架上时，静止状态下其各处的张力为T0(N·m-1)，当声波传至振膜时，振膜在声压的作用下会产生振动，振膜中心位置的振幅最大，而边缘位置的振幅最小为0。由于薄膜振幅很小，振膜振动时其边缘处的张力仍为T0，圆形振膜振动示意图如图1所示。

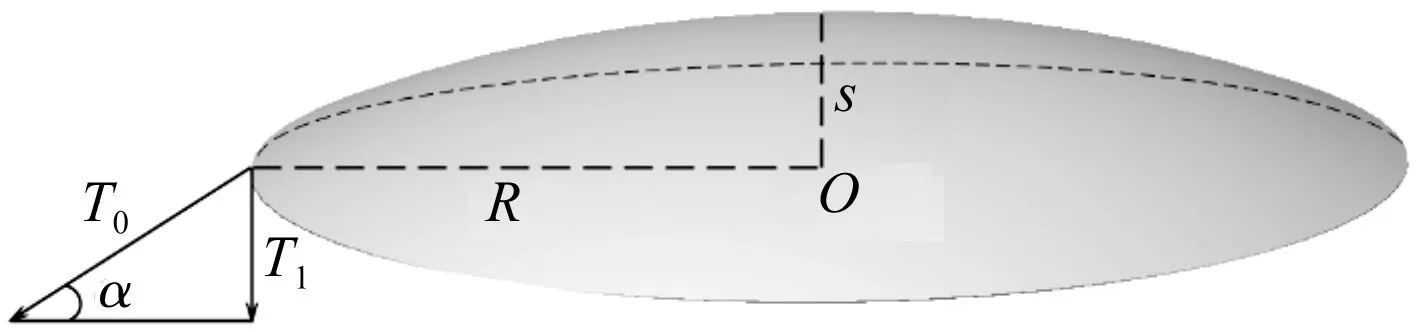
图1 圆形振膜振动示意图

振膜振动时对其边缘的作用力，即回复力F1为：

F1=-2πRT1=-2πRT0sinα=-2πT0s

(1)

式中：R—振膜的半径；α—振膜振动时张力方向与其静止状态的直径夹角；s—振膜的振幅大小。

振膜振动时受到的空气阻力F2为：

(2)

式中：η—空气的粘滞系数。

不妨假设声压为P=P0sinωt，则振膜所受到的声压作用力F3为：

F3=(πR2)P0sinωt

(3)

根据牛顿第二定律，联立式(1～3)可以得到振膜振动的微分方程[13]为：

(4)

式中：σ—振膜单位面积的质量，且满足σ=hρ；h—振膜的厚度；ρ—振膜材料的密度。

化简可得：

(5)

则其一阶谐振频率为：

(6)

由式(6)可知，圆形振膜的一阶谐振频率与其半径、厚度成反比关系，振膜半径越大、厚度越厚，则一阶谐振频率越低，容易出现共振现象，导致声谐振频率越高，这样薄膜的频率响应特性越好。

1.2 方形振膜振动理论

由矩形薄膜自由振动的基本原理[15]可知，方形振膜的一阶谐振频率为：

(7)

式中：a—方形振膜的边长；m,n—正整数，表示方形振膜振动的节线数。

若令m=n=1，即可得到方形振膜的最低一阶谐振频率为：

(8)

2 条纹位移测量原理

条纹位移测量是利用高速相机成像，通过条纹的密度变化提取振动的位移信息。笔者将条纹附在薄膜表面，形成条纹薄膜。薄膜在声压的作用下，其表面的条纹密度会随着振动发生变化，条纹的频率信息也会发生变化。

由于薄膜四周被固定，其表面中心位置条纹的中心线密度变化呈现微小的线性变化，但考虑到薄膜中心位置的位移足够小，笔者近似地将薄膜振动视为平动变化，于是可以通过傅里叶变换对薄膜表面的条纹信号进行分析[16]。同时，结合频谱校正方法对条纹信号的频率进行校正[17]，得到条纹信号的真实频率信息，实现薄膜振动信息的提取，从而实现低频振动的测量，如图2所示。

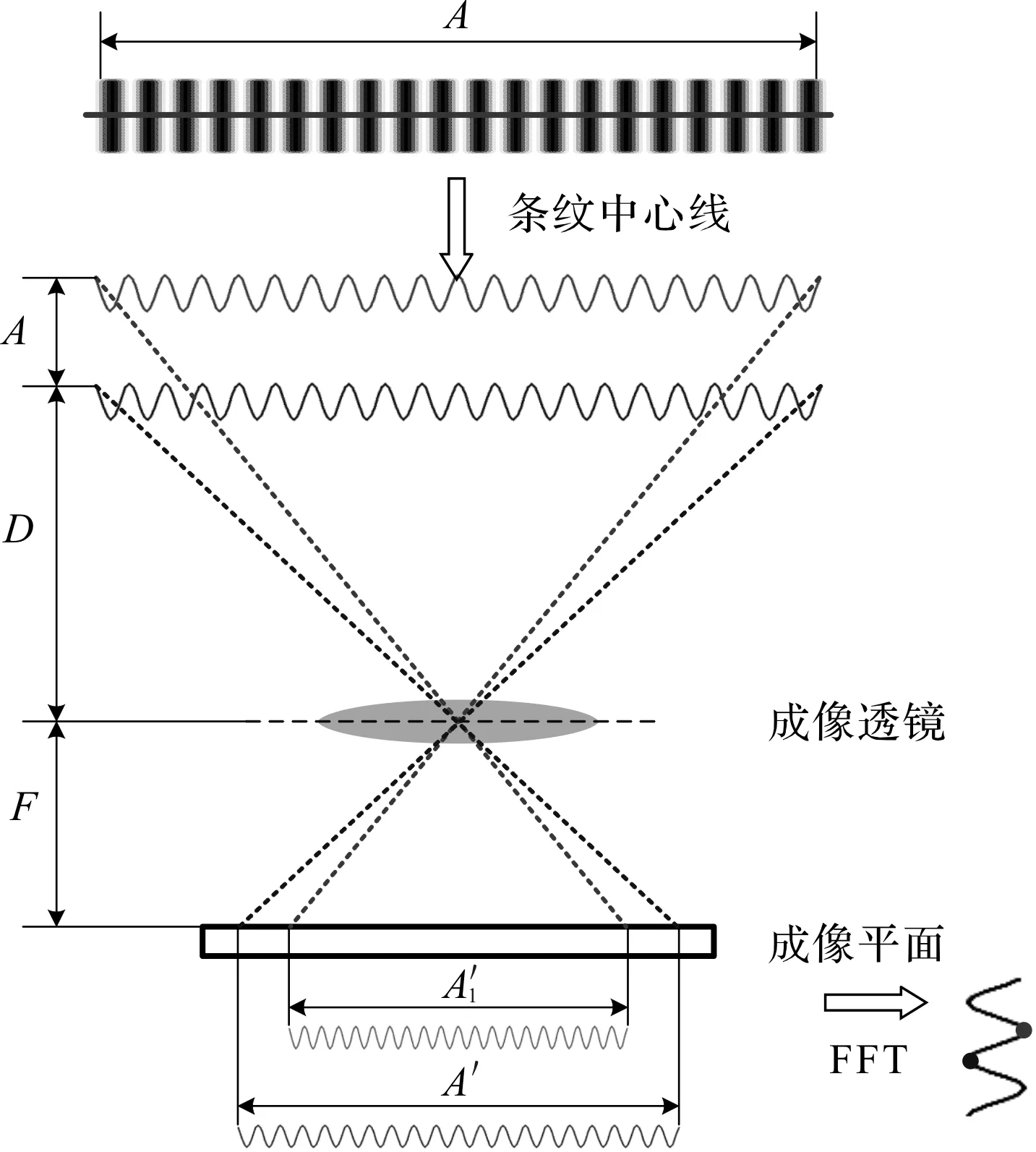
图2 条纹位移测量原理图A-条纹的实际长度；A′-条纹初始位置的成像长度；D-物距；F-像距，即透镜与成像平面之间的距离；ΔA-条纹与初始位置之间的位移；对应的成像长度

由成像原理可得：

(9)

(10)

由透镜的成像关系可得：

(11)

(12)

式中：f—透镜焦距；M—成像的放大因子。

由式(9～10)，可知

D=f(1+M)

(13)

联立以上各式，可得薄膜在t时刻振动的振幅为：

(14)

式中：a(t)—条纹在t时刻的成像条纹密度；a0—条纹初始位置对应的成像条纹密度。

由式(14)可知：在透镜焦距f与成像的放大因子一定的情况下，只需要知道初始位置的成像条纹密度及其在t时刻的密度变化，即可得到薄膜在t时刻振动的振幅。

3 条纹薄膜的性能研究

3.1 COMSOL仿真模型

笔者利用COMSOL Multiphysics建立仿真模型。该软件具有振动声学的接口，可以自定义点声源激励，薄膜在点声源声压的作用下将产生振动。模型可被简化为一个包含压力声学和壳单元2个物理接口的声壳耦合问题；同时笔者将薄膜简化为一个边界固定的圆形外壳，在其周围定义一个球形空气域，球形域内部包含一个点声源。

笔者对球形域边界应用球面波辐射条件，这样可以将整个声场视为没有界限，有限元仿真模型示意图，如图3所示。

图3 有限元仿真模型示意图

3.2 实验装置

本研究采用模拟仿真与实验分析相结合的方法，研究薄膜的形状、材料、厚度、直径大小、条纹打印质量、条纹密度以及条纹采样分辨率对测量性能的影响。

条纹薄膜性能实验装置如图4所示。

图4 条纹薄膜性能实验装置图

图4中，采用型号为 PCO.1 200 hs的CMOS高速相机，将其固定在三脚架上，调整成像镜头正对着条纹薄膜。薄膜通过夹具固定在工作台上，采用扬声器激励，扬声器由信号发生器(Agilent 33220)输出激励信号的幅值和频率进行控制。

3.3 COMSOL仿真与实验结果分析

3.3.1 形状对测量性能的影响

通常情况下，大多数振动膜都是设计成圆形和方形结构[18]。为了研究这两种薄膜形状对低频声音测量性能的影响，笔者先运用COMSOL软件分别对直径φ=50 mm、边长a=50 mm、厚度h=70 μm的圆形和方形的PET薄膜进行应力分析，接着利用图4实验装置，采用0～250 Hz的扫频信号对两种形状薄膜进行激励，扫频时间为10 s，结果如图5所示。

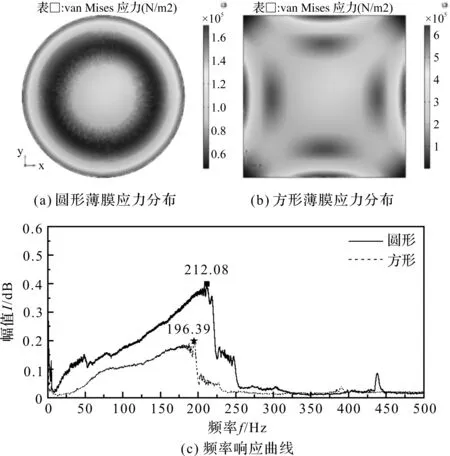
图5 两种形状薄膜的应力分布与频率响应曲线

薄膜参数：弹性模量E=2.96 GPa；泊松比v=0.37；密度ρ=1 420 kg/m3。

从图5可知：(1)圆形薄膜表面沿圆周方向应力分布均匀，而且在垂直圆周方向的应力分布呈阶梯状变化，无应力集中点；(2)方形薄膜表面的应力分布不均匀，且在薄膜四周边沿的中间位置处容易产生应力集中；(3)两种形状薄膜的频率响应范围均在0～200 Hz左右，而圆形薄膜的响应幅值比方形薄膜的大，说明圆形薄膜的频响效果更好。因此，笔者将条纹薄膜设计成圆形。

通过式(6～7)、COMSOL有限元仿真和实验，得到的圆形和方形薄膜的一阶谐振频率结果，如表1所示。

表1 圆形和方形薄膜的一阶谐振频率结果 (单位：Hz)

由表1可知：两种薄膜的理论、仿真和实验一阶谐振频率基本吻合，验证了仿真与实验结果的准确性。

3.3.2 材料对测量性能的影响

为了研究不同材料、厚度和直径大小的振膜对测量性能的影响，笔者采用图4实验装置，采用条纹密度为10周期/cm、直径为φ=40 mm、厚度为h=85 μm的PET膜和双胶纸；双胶纸的参数如下：弹性模量E=634 MPa，泊松比v=0.34，密度ρ=1 400 kg/m3，分别用0～250 Hz的扫频信号激励，高速相机的采样频率为fs=2 kHz。得到的结果如图6所示。

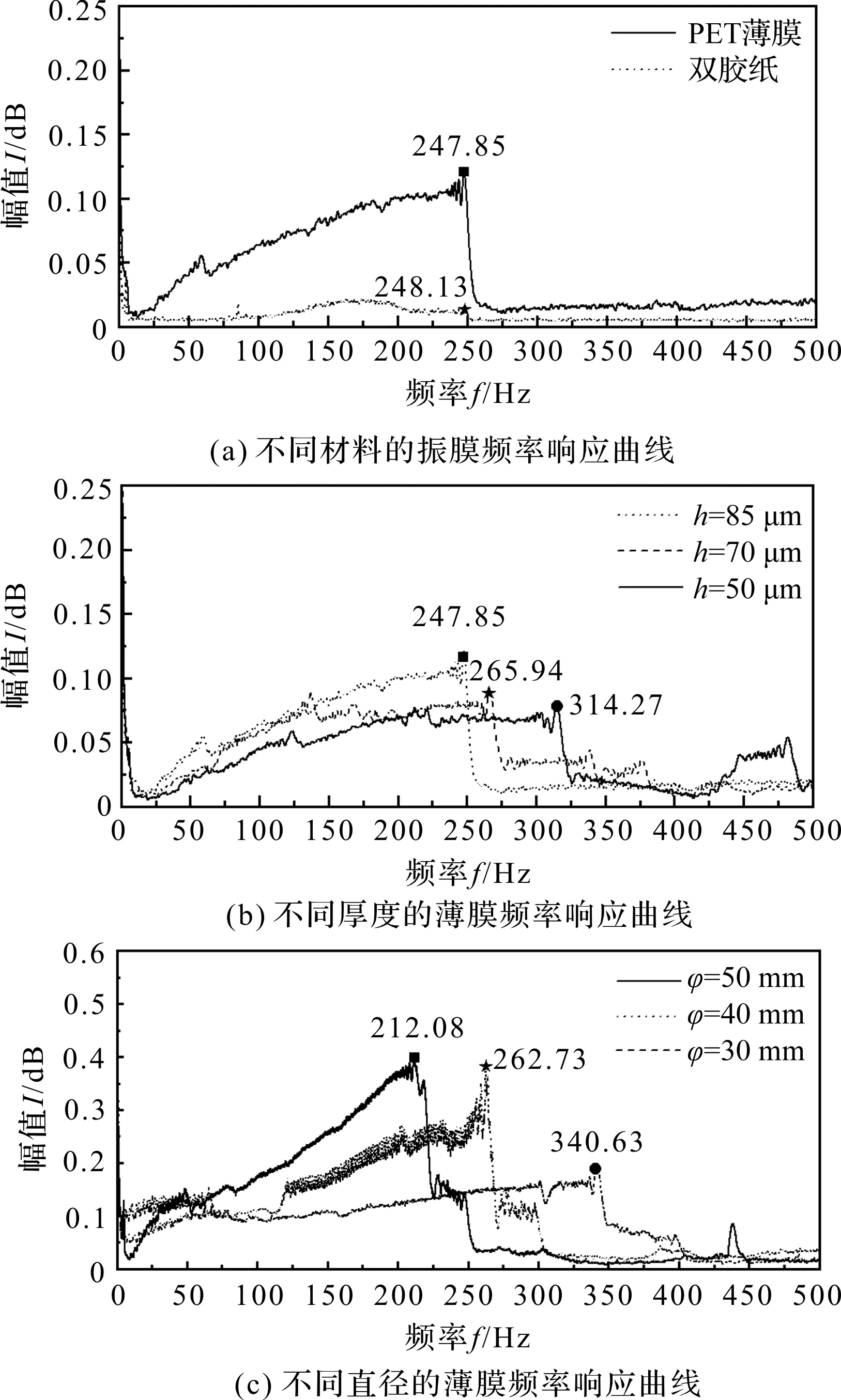
图6 不同材料、厚度和直径的薄膜频率响应曲线

图6可知：不同材料的振膜频率响应曲线不同；PET薄膜的响应幅值比双胶纸的大，双胶纸的响应幅值最高不超过0.025。这说明用双胶纸制作条纹薄膜，达不到低频声音的测量效果。

同理，分别通过式(6)、COMSOL有限元模拟仿真和实验，得到PET薄膜和双胶纸的一阶谐振频率结果，如表2所示。

表2 PET薄膜和双胶纸的一阶谐振频率结果(单位：Hz)

由表2可知：PET薄膜和双胶纸的理论、仿真和实验一阶谐振频率基本吻合。结合图6实验结果，笔者利用PET薄膜制作条纹薄膜。

3.3.3 厚度对测量性能的影响

振膜的一阶谐振频率会随着其厚度的变化而变化，因此笔者采用条纹密度为10周期/cm，直径为φ=40 mm，厚度分别为85 μm、70 μm和50 μm的PET薄膜，用0～500 Hz的扫频信号激励，高速相机的采样频率为fs=2 kHz，以研究不同厚度对测试性能的影响。

由图6(b)可知：随着振膜厚度的减小，其一阶谐振频率逐渐增大。分别通过式(6)、COMSOL有限元模拟仿真和实验得到3种不同厚度下PET薄膜的一阶谐振频率结果，如表3所示。

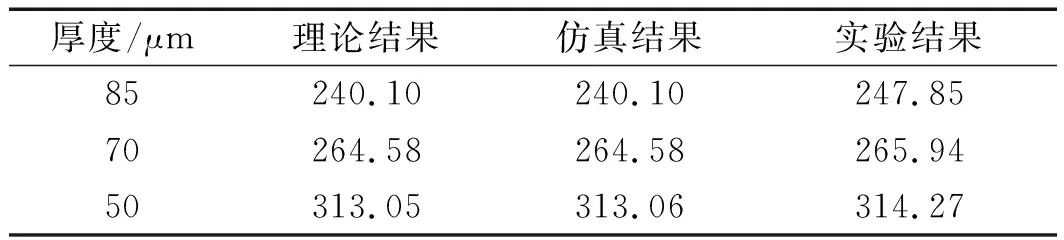
表3 85 μm、70 μm和50 μm薄膜的一阶谐振频率结果 (单位：Hz)

由表3可知：不同厚度下PET薄膜理论、仿真与实验所得到的一阶谐振频率基本吻合。

因此，在其他条件一定的情况下，应尽可能地选择厚度薄的振膜，以得到更宽的频率响应范围。

3.3.4 直径大小对测量性能的影响

同样，由式(6)可知：振膜的一阶谐振频率会随着其直径大小的变化而变化，采用条纹密度为12周期/cm，厚度为h=70 μm的PET膜，直径分别为30 mm、40 mm和50 mm的PET薄膜，分别用扫频信号激励，高速相机的采样频率为fs=2 kHz，以研究不同直径大小对测试性能的影响。

由图6(c)可知：随着半径的增大，其频率响应范围逐渐减小，且频率响应范围均不低于200 Hz。而且，随着直径的增大，薄膜的响应幅值不断增大，即频率响应的效果逐渐提高。

分别通过式(6)、COMSOL有限元模拟仿真和实验得到不同直径大小PET薄膜的一阶谐振频率结果如表4所示。

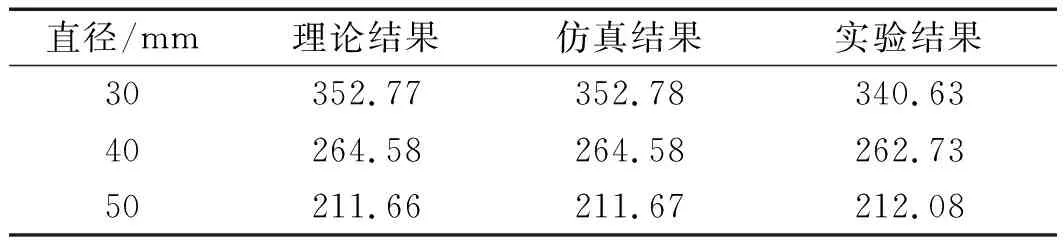
表4 30 mm、40 mm和50 mm薄膜的一阶谐振频率结果 (单位：Hz)

由表4也可直观看出，不同直径下PET薄膜理论、仿真与实验所得到的一阶谐振频率基本吻合。

本研究设计的条纹薄膜直径为φ=50 mm，这样既能满足一定的频率响应范围，同时又能保证薄膜频响效果。

3.3.5 条纹打印质量对测量性能的影响

如果相机拍摄的条纹信号存在噪声，则会影响图像的识别精度，进而影响薄膜振动信息的提取精度，因此，应尽量减小由于薄膜表面初始条纹的打印质量不高引入的噪声。笔者利用MATLAB编写的条纹生成函数生成条纹，采用喷墨打印机将生成的条纹打印在PET薄膜表面，以减小自身引入的噪声，在一定程度上提高了条纹图像的识别精度和薄膜振动信息的提取精度。

3.3.6 条纹密度对测量性能的影响

笔者采用图4所示的实验装置，得到了不同条纹密度和像素点数的振膜对测量性能的影响，如图7所示。

图7 不同条纹密度与像素点数的薄膜中心位置振动位移图

在相机能够分辨条纹的情况下，笔者采用直径φ=50 mm、厚度h=25 μm的PET膜，在固定频率f=175 Hz的激励下，高速相机采样频率为fs=2 kHz，分别设置了5周期/cm、6.66周期/cm、10周期/cm以及20周期/cm等4组不同条纹密度，研究条纹密度对振膜测量性能的影响，。

由图7(a)可知：初始条纹密度越小，在薄膜中心位置测量的位移曲线噪声越大，相应的误差也越大；反之，所得到的位移曲线越平滑、噪声越小，测量精度也越高。

综上所述，所研究的条纹薄膜参数为：直径为φ=50 mm、厚度为h=50 μm的圆形PET薄膜；条纹周期密度为20周期/cm的正弦条纹。

3.3.7 条纹采样分辨率对测量性能的影响

通常相机中图像传感器的物理尺寸和像素分辨率是固定的。由图2和式(9)可知：当条纹薄膜的密度和长度一定时，对于固定的透镜，条纹在高速相机上的成像范围随着物距D的增加而减小。

为了研究条纹采样分辨率对条纹薄膜测量低频声音的影响，笔者采用条纹密度为20周期/cm、直径φ=50 mm、厚度h=70 μm的PET膜，在固定频率f=205 Hz的激励下，高速相机采样频率为fs=2 kHz，研究像素点数N分别为70、270、470和670的薄膜中心位置振动的测量结果。

由图7(b)可知：对于同一密度条纹，随着相机像素点数N的增加，所得到薄膜中心位置的振动位移曲线越平滑，测量精度也越高。因此，在实际测量中，应使尽量多的像素点用于薄膜条纹的成像，以提高测量精度。

4 条纹薄膜在梁模态分析中的应用

为了验证条纹薄膜能有效地测量低频声音，笔者将所研究的条纹薄膜应用在横梁的模态分析中，进行实验验证。

笔者搭建的实验装置如图8所示。

图8 横梁模态分析实验装置图

分析结果如图9所示。

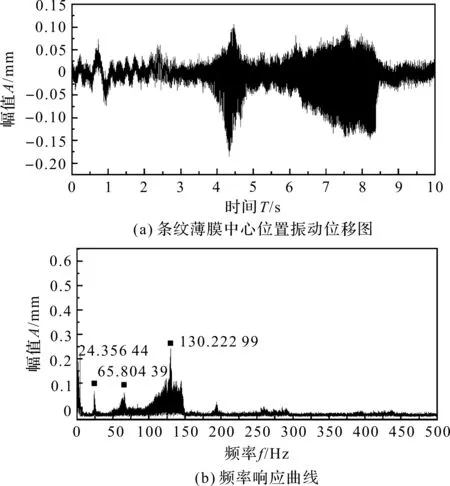
图9 横梁振动模态分析结果

实验中，笔者采用的横梁尺寸为500 mm×40 mm×1.2 mm，其一端固定在工作台上，另一端固定在激振器(TIRA GmbH，德国)的输出端，激振器的振动幅值和频率由信号发生器(Agilent 33220)输出一段时长为10 s，功率为500 mV，频率0～150 Hz的扫频信号，并经过功率放大器后再输入激振器中。

首先，笔者通过COMSOL Multiphysics有限元模拟仿真，得到横梁的前三阶共振频率分别为f1=24.218 Hz、f2=66.765 Hz、f3=130.99 Hz。实验中，将条纹薄膜通过夹具放置在距离激振器一端5/7位置，利用采样频率为fs=2 kHz的CMOS高速相机进行采集，得到条纹薄膜中心位置的振动位移和频率响应曲线。

由图8可知：利用条纹薄膜测量得到横梁的前三阶共振频率分别为f1=24.36 Hz、f2=65.80 Hz、f3=130.22 Hz，与仿真结果基本吻合，从而验证了所设计的条纹薄膜对低频声音能进行准确性测量。

5 结束语

为了避免传感器自身重量影响结构的模态参数，笔者提出了基于条纹薄膜的测量理论和方法，以实现非接触式振动测量；结合有限元模拟仿真和实验分析、探讨了薄膜的形状、材料、厚度、直径大小等因素对测量性能的影响；利用傅里叶变换，对薄膜表面的条纹信号进行了分析，并结合频谱校正方法对条纹频谱信号进行了校正，研究了低频振动测量的条纹薄膜；其次，笔者将条纹薄膜应用在梁结构的模态分析中。

实验结果表明：利用条纹薄膜测量得到横梁的前三阶固有频率与仿真结果基本吻合；该测量方法简单有效，具有很好的工程应用前景。