电容式微超声换能器等效电路模型与阵元优化
张 慧,石建超,张 雯,曾周末,綦 磊
电容式微超声换能器等效电路模型与阵元优化
张 慧1,石建超1,张 雯1,曾周末1,綦 磊2
(1.天津大学精密测试技术与仪器国家重点实验室,天津 300072;2. 北京卫星环境工程研究所,北京100094)
针对电容式微超声换能器(CMUT)建立了非线性等效电路模型. 以声源表面运动方程为理论基础,将CMUT的声学、力学参数等效成电学元器件,分别建立CMUT单振膜与多振膜阵元的等效电路模型,分析多振膜阵元中振膜间的声场干扰,计算了振膜的辐射阻抗;并且在模型中构造了辐射阻抗等效RLC电路. 利用SPICE软件对CMUT的等效电路模型进行仿真分析,得出了CMUT振膜的振动位移幅值频域响应;通过多普勒测振系统测量多膜CMUT阵元中不同位置振膜的频率响应,验证了所建立模型的正确性. 利用该非线性等效电路模型,对2×2、3×3与4×4这3种方形排布的CMUT阵元进行优化设计,得到了3种规模阵元振膜的最佳间距分别为230,mm、160,mm与130,mm.
微机电系统;电容式微超声换能器;非线性等效电路模型;辐射阻抗
近年来,随着MEMS技术的蓬勃发展,电容式微超声换能器(capacitive micromachined ultrasonic transducer,CMUT)的研究成为热点,在医用内窥成像、治疗超声、微流体探测、工业无损检测等方面具有重要的应用前景.研究中通常使用有限元方法对CMUT进行设计仿真[1].有限元方法计算时间长、换能器阵列建模复杂,不适合高效快捷地设计结构参数以及仿真大规模阵列.等效电路模型以解析模型[2-3]为基础,计算时间短,对换能器阵列建模相对简单,可以弥补有限元方法的不足.
等效电路模型将机电换能器的声学、力学参数等效成电学元器件,并通过建立解析数学方程式构造电路.Mason[4]在20世纪40年代提出了等效电路模型,利用电路分析方法对机电传感器进行力电特性的仿真分析.美国斯坦福大学对处于接收模式下的换能器进行了小信号模型分析,建立了CMUT等效电路模型,并且,对处于发射模式下的换能器特性进行了简单的非线性解析,但是没有建立发射模式的等效电路模型[5].德国不莱梅大学建立了发射模式的等效电路模型,并且提出了活塞简化模型,但是没有分析计算多振膜间的互辐射阻抗[6].土耳其比尔肯大学拓展了梅森模型,建立了线性与非线性等效电路模型,对单个CMUT振膜(简称单膜)进行了仿真分 析[7-8],在该模型中,没有分析振膜辐射阻抗,探讨辐射阻抗的频率响应.
环形阵列与二维阵列的阵元通常由多个换能器单元并联而成,阵元中换能器振膜的顶电极相互连接,振膜排布方式以方形为主,这样的阵元可称为多膜CMUT阵元.
本文首先以声源表面的运动方程为基础,结合实际设计制作的电容式微超声换能器的结构特征,建立单膜非线性等效电路模型,设计了阻抗等效RLC电路以便于SPICE仿真;其次分析振膜之间的声场干扰,建立多膜CMUT阵元等效电路模型,提出方形排布的多膜CMUT阵元中振膜辐射阻抗计算简化算法,对制造的CMUT进行测试,验证了模型的正确性;最后利用非线性等效电路模型,仿真分析了3种方形排布的多膜CMUT阵元中振膜间距对辐射阻抗的影响,实现了CMUT阵元的优化设计.
1 非线性等效电路模型
1.1 单膜非线性等效电路模型
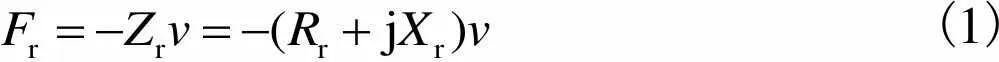
(1)
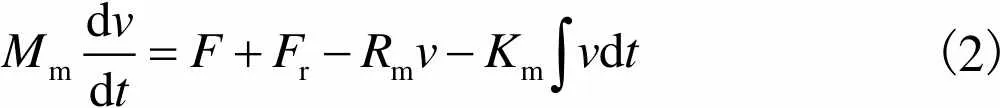
(2)
将方程(2)中的力学量转化为相关的等效电学量,构成CMUT力学回路.
CMUT振膜在直流偏压与交流激励的共同作用下振动发出超声波,电容电荷量的变化等于流过的电流[8],即
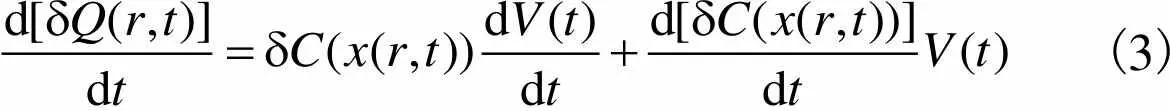
(3)
式(3)是CMUT电学回路的基础公式.等号右侧第1项为交流电流产生电流,简称交变电流;第2项为电容量的变化产生的电流,简称容变电流,反映了器件将电能转化为声能的能力.
以式(2)与式(3)为基础,CMUT电学回路与力学回路构成了单膜非线性等效电路,如图1所示.其中为静态电容值,为交变电流,为容变电流,为振膜受到的电场力,c为振膜受到的弹性力,为振膜等效质量,为振膜力顺值,与振膜弹性系数负相关[10],为振膜辐射阻抗,p()为圆膜中心点振动位移幅值,=vel/tot.
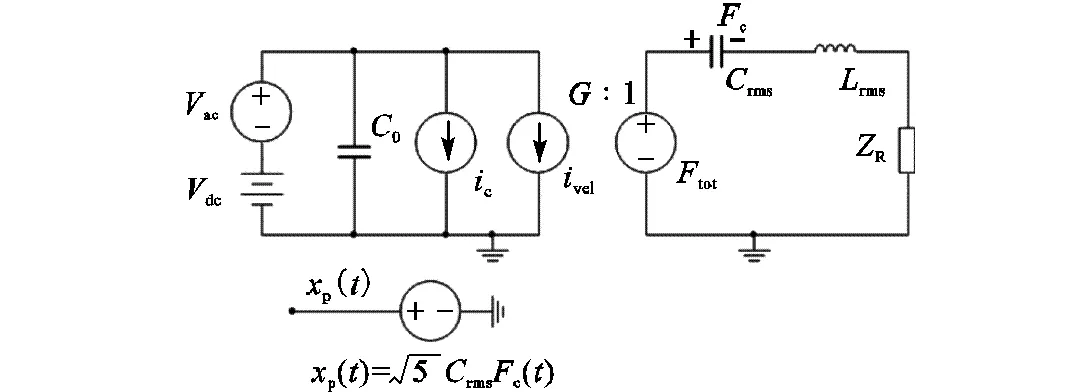
图1 单膜非线性等效电路模型
单膜非线性等效电路反映了CMUT在工作状态下电、力、声系统之间的能量转化,其力学回路方程与电学回路方程都是非线性方程,参数计算引入了器件的非线性特性[8].模型中振膜形状为圆形,在极坐标中,圆心距为的微圆环产生的交变电流为
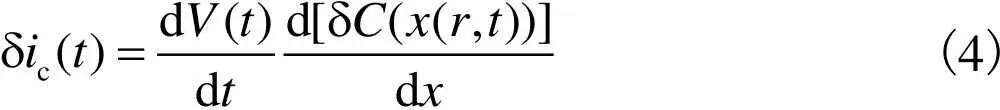
(4)
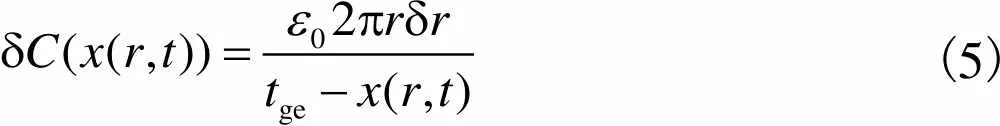
(5)
电容式微超声换能器的金属顶电极覆盖在振膜的上方,金属顶电极面积为换能器振动薄膜面积的1/2时,换能器具有较低的吸合电压和较大带宽值及机电耦合系数.由于实际设计、制作的换能器顶电极面积约为振膜面积的1/2,因此换能器的初始电容为.将式(5)代入式(4)中,计算交变电流,积分范围由0到,为振膜半径,因此有
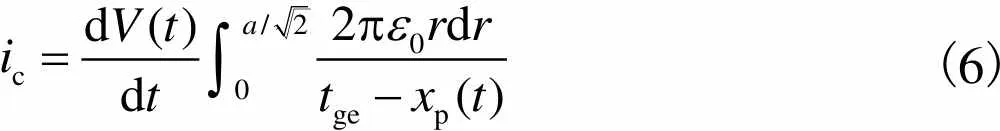
(6)
求解积分得到交变电流的表达式为
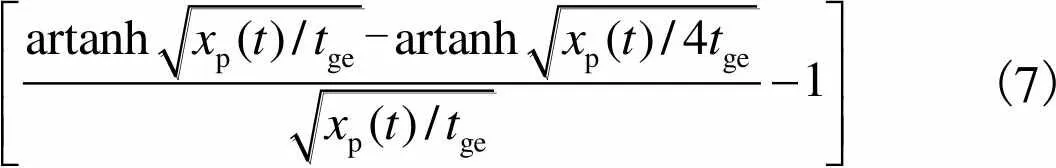
(7)
同时,积分计算容变电流得
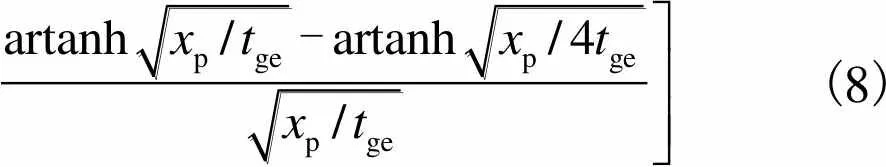
(8)
辐射阻抗的计算精度直接决定了非线性等效电路模型的仿真精度,在单膜非线性等效电路模型中,只需计算单膜自辐射阻抗[11-13]即
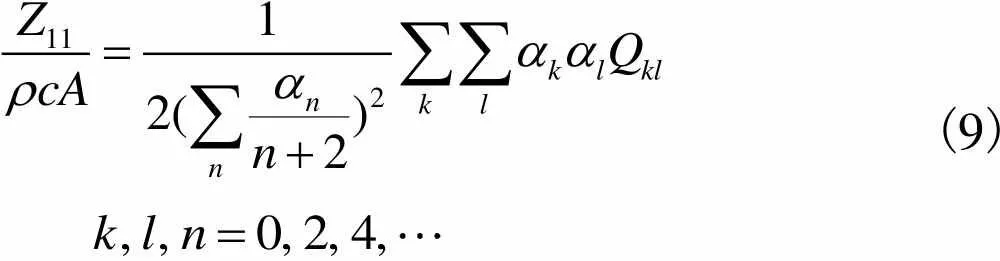
(9)
振膜辐射阻抗会随频率变化,为便于仿真其频域特性,设计了RLC电路等效原辐射阻抗.RLC等效电路如图2(a)所示,左边部分等效自辐射阻抗,右边等效互辐射阻抗.RLC电路参数由Nelder-Mead非线性规划算法确定,其频响拟合结果如图2(b)所示.
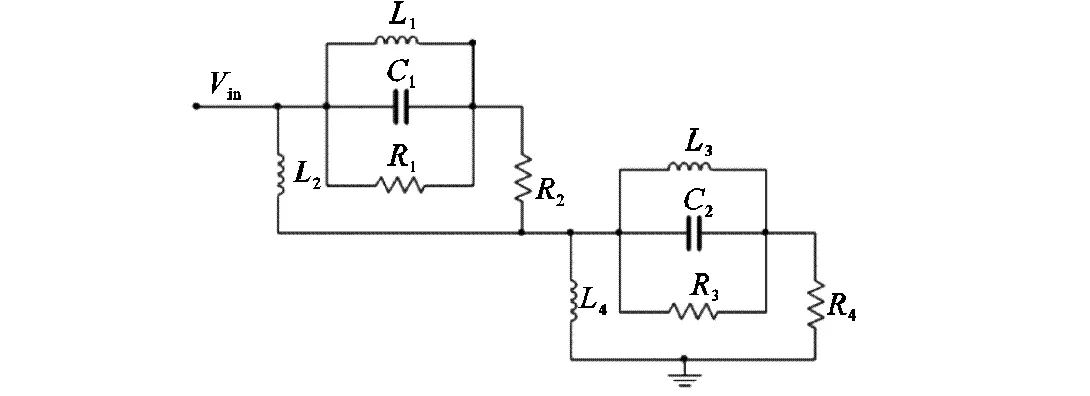
(a)阻抗等效RLC电路
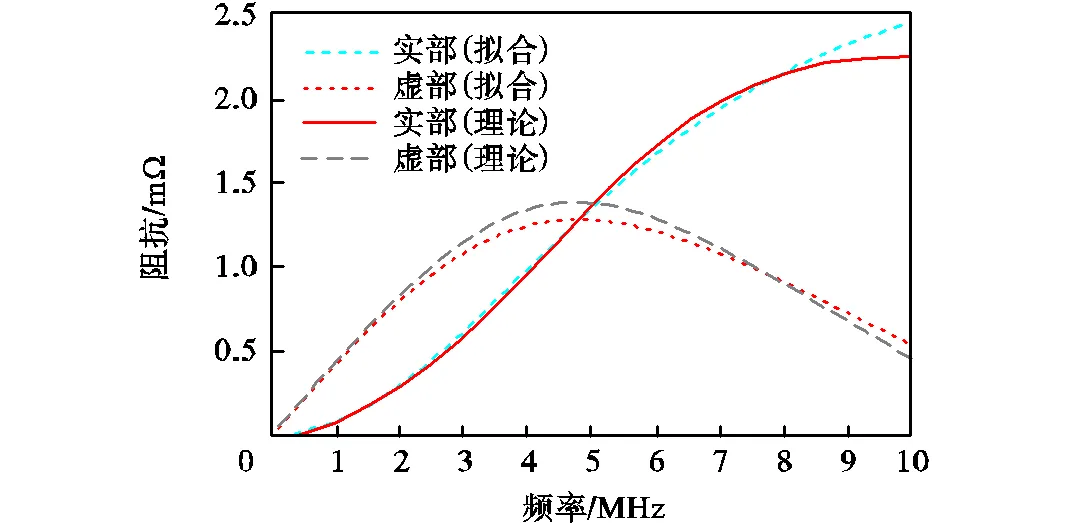
(b)频响拟合结果
图2 阻抗等效RLC电路及频响拟合结果
Fig.2 RLC circuit of the radiation impedance and fitting results of frequency response
由此,构造图1中等效电路,利用SPICE软件对单膜非线性等效电路模型进行直流分析、交流分析与瞬态分析,得到CMUT的时序与频率响应[14-15].
1.2 多膜CMUT非线性等效电路模型
对于多膜CMUT阵元,振膜之间发射声场产生相互作用,如图3所示,振膜2发射声压对振膜1作用产生的辐射阻抗为,称为互辐射阻抗,为计算更加精确的振膜辐射阻抗,引入互辐射阻抗,得到多膜阵元各振膜的受力计算公式为
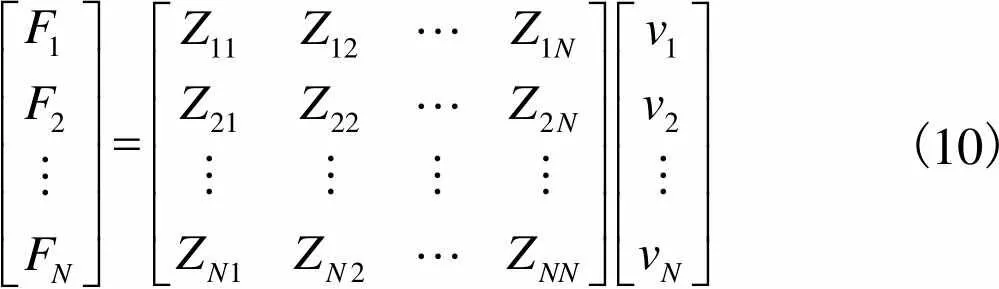
(10)
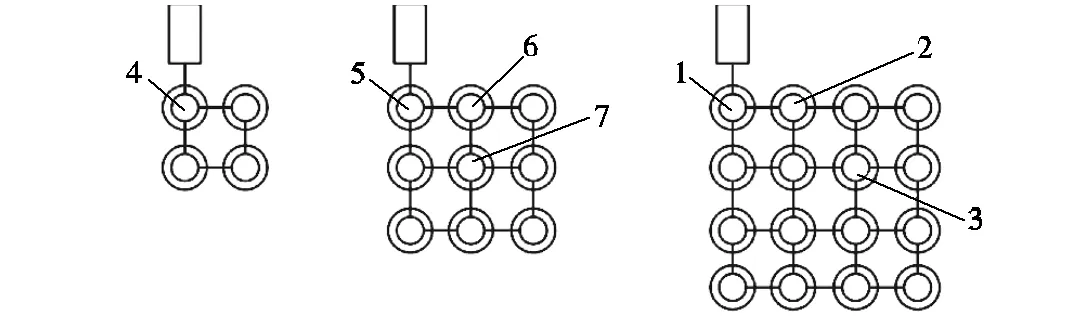
(a)2×2阵元 (b)3×3阵元 (c)4×4阵元
图3 2×2、3×3、4×4多膜CMUT阵元示意
Fig.3 Three types of CMUT elements whose cells are arranged in 2×2,3×3 and 4×4 square array
对于方形排布的多膜CMUT阵元,简化阻抗矩阵.如图3所示,在4×4多膜阵元中,根据振膜所处的位置不同,将其分为3类,编号为1、2、3,阵元角上4个振膜都编号为1,阵元中心的4个振膜都编号为3,其余振膜编号为2,相同编号的振膜辐射阻抗相同.式(10)中的振膜受力表达式可简化为
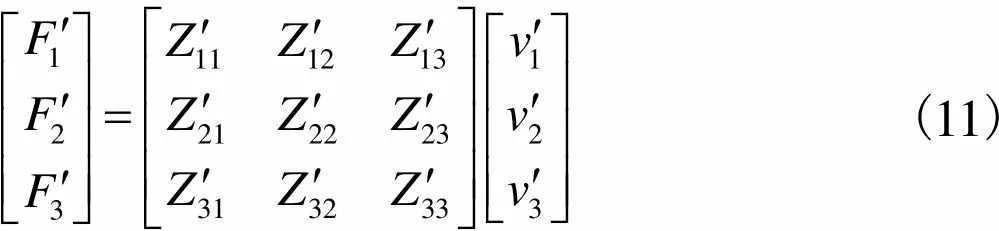
(11)
同类膜具有相等的辐射阻抗与振动速度,可以统一计算.式(11)中阻抗矩阵的第1列,表示膜1的自辐射阻抗,表示膜1与所有膜2的互辐射阻抗之和,表示膜1与所有膜3的互辐射阻抗之和;下面两列以此类推.式(10)中阻抗矩阵元素与式(11)中阻抗矩阵元素的转化关系为
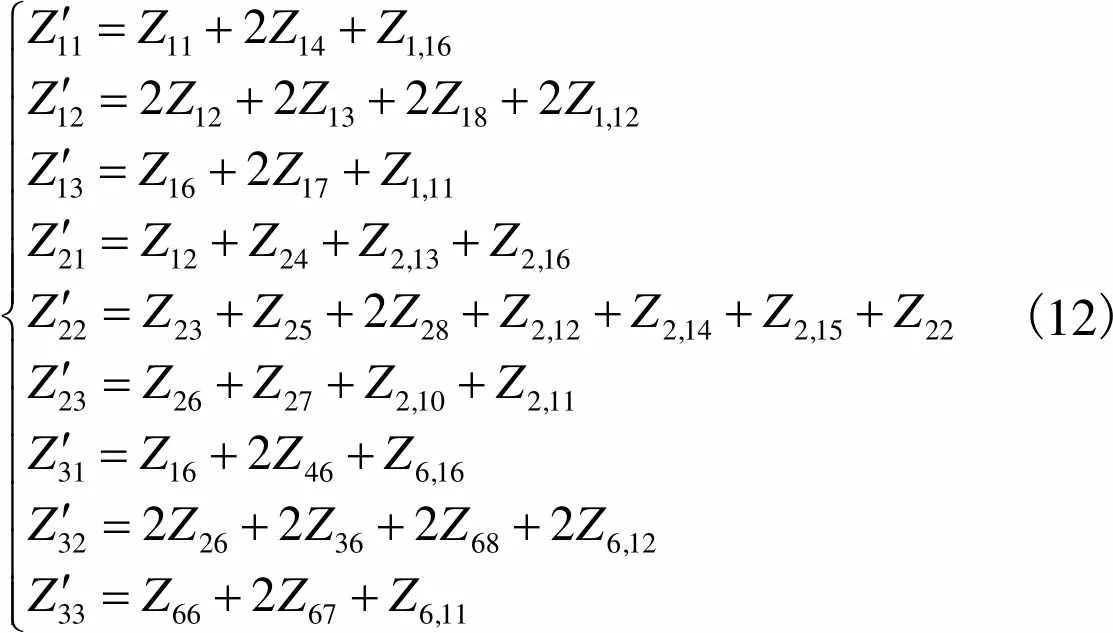
(12)
对于其他规模的阵元,如图3所示,也可对振膜进行分类并做相应简化.

(13)

(14)
根据式(13),计算方形排布的多膜CMUT阵元中的振膜的辐射阻抗,并与单膜辐射阻抗进行比较,如图4所示,阵元中的振膜的辐射阻抗频响曲线整体波动变大,虚部的峰值也发生了移动.
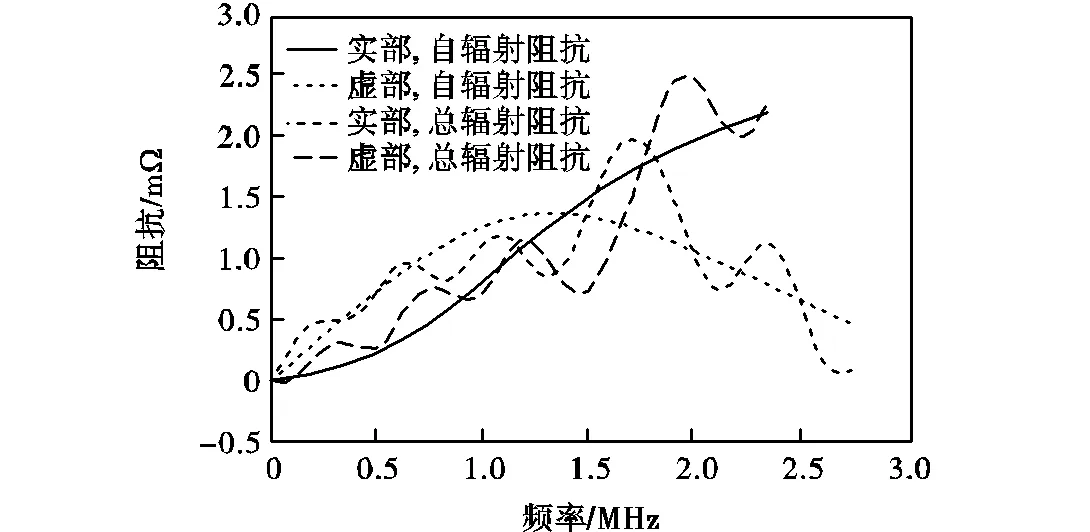
图4阵元中振膜辐射阻抗与单膜辐射阻抗的比较
Fig.4 Comparison of radiation impedance frequency re-sponse between the single cell and the cells in the ele-ment
根据式(10)~式(13),计算多膜CMUT阵元中振膜的辐射阻抗,进行等效电路仿真,可以得到振膜频响特性.
2 验 证
应用多普勒测振系统测试4×4多膜CMUT阵元,对模型仿真结果进行验证.
多普勒测振系统(如图5所示)主要用来测试在发射模式下CMUT振膜振动幅值的频域响应.测试时,信号发生器发送10,V正弦交流扫频信号,交流信号与50,V直流偏压通过T型偏置器耦合,施加在CMUT两端.经过控制器解码输出关于振动位移的模拟信号,然后由NI板卡PXI-5122转换与采集数据并将数据传输至计算机中.
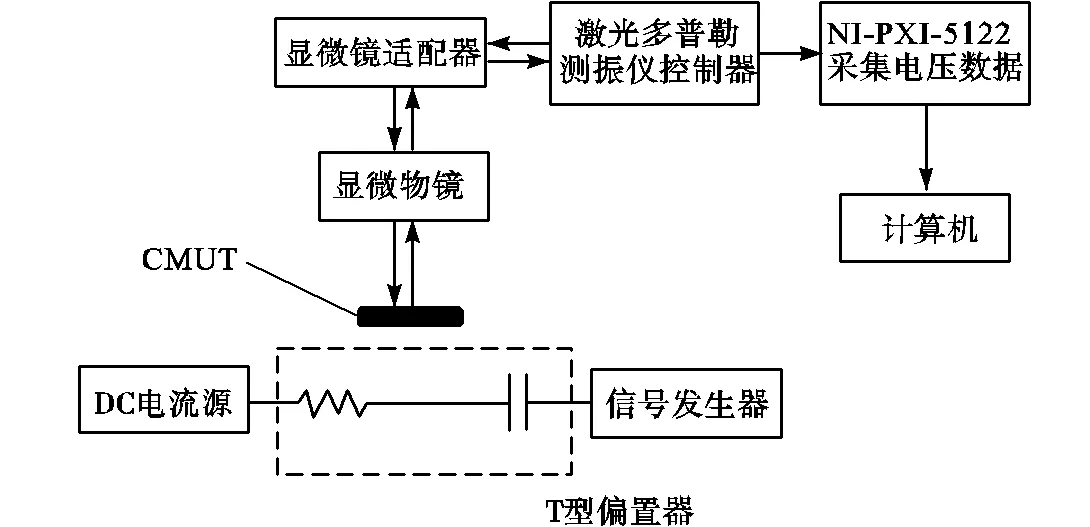
图5 多普勒测振系统
加工制作CMUT阵列,每个阵列由8×8个阵元构成,每个阵元由4×4个圆形振膜单元并联组成.相关参数见表1.通过多膜CMUT非线性等效电路模型的仿真得到4×4阵元中3种振膜的频响曲线,如图6所示,3种振膜的共振频率不同,分别为1.84,MHz、1.81,MHz和1.72,MHz.
表1 多膜CMUT阵元相关参数

Tab.1 Parameters of the multi-cell CMUT element
如图6所示,实验测得振膜1、2、3的共振频率分别为1.84,MHz、1.80,MHz和1.64,MHz.在4×4阵元中,靠近中心的振膜共振频率略低于靠近边缘的振膜共振频率,因为靠近中心的振膜与其他振膜的距离较小,对其产生影响的振膜较多,所以振膜共振频率偏移较大.实验所得数据趋势与仿真相同,验证了非线性等效电路模型的正确性.另外,利用单膜非线性等效电路模型对振膜位移频率响应进行了仿真,得到振膜共振频率为2.08,MHz,与实验测试共振频率相差较大,相比之下多膜CMUT非线性等效电路模型的结果更接近实验测试数据.
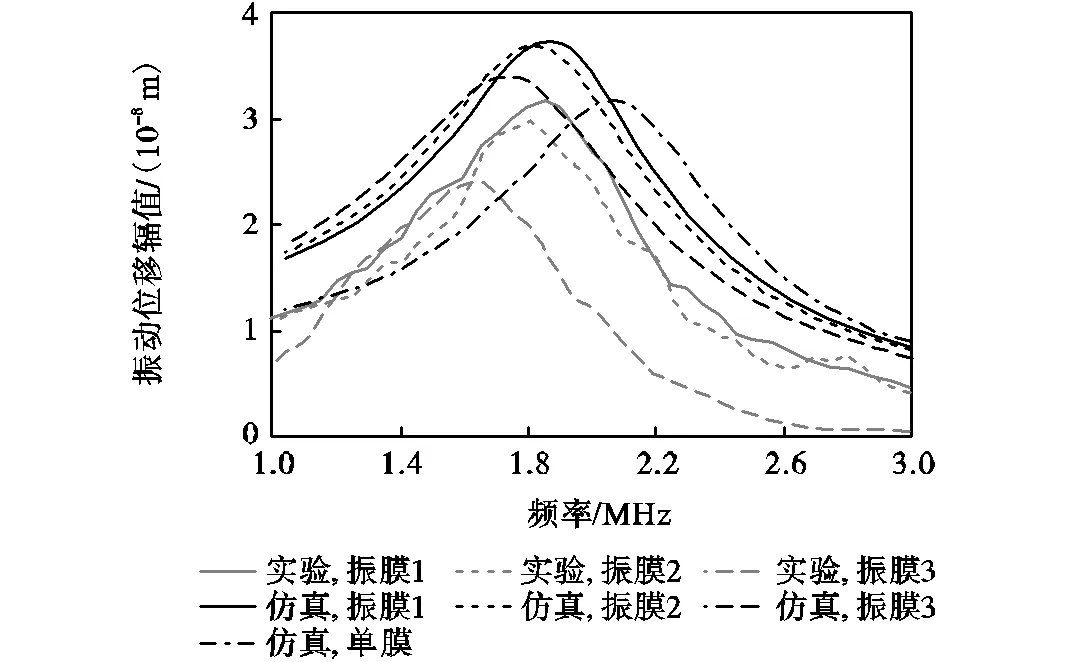
图6非线性等效电路模型仿真与测试的位移频响曲线
Fig.6 Comparison of center displacement amplitude frequency response generated by the nonlinear equivalent circuit and the experiment
3 多膜CMUT阵元的优化设计
借助非线性等效电路模型仿真,分析不同振膜间距、不同规模的阵元的共振频率与辐射声压的变化规律,可以优化阵元的振膜排列分布.
阵元振膜的发射声压取决于振膜的辐射阻抗的大小.阵元的规模越大,整体发射声压也就越大.但是在阵列设计中,阵元规模是有上限的,它不能大于阵元间距,并且大规模阵元的加工难度大.因此本次阵元优化的目的就是设计较小规模的阵元,实现最大发射声压的输出.
针对上述目的,设计3种CMUT阵元,阵元规模依次为2×2、3×3、4×4,如图3所示.在这3种规模CMUT阵元中,分别包含1~7共7种不同位置的CMUT振膜(3×3阵元编号方法与4×4阵元相同,2×2阵元只有一类膜,编号为4).
图7给出了振膜1~7的辐射阻抗随振膜间距变化曲线.当间距较小时,振膜辐射阻抗波动较大;随着间距逐渐增加,阵元振膜互辐射阻抗值逐渐趋于零,总辐射阻抗值收敛于单膜自辐射阻抗值.辐射阻抗越大,由式(1)可知,振膜受到声场的反作用力越大,释放超声能量越大.计算得到阵元振膜辐射阻抗-间距曲线,当辐射阻抗达到最大时,阵元间距最佳.
对于2×2阵元振膜,振膜半径为65,mm时,响应共振频率1.85,MHz,阵元中只有一类膜(振膜4),可以依据单一振膜频响曲线判断最佳间距值,由图7(a)得到振膜最佳间距为230,mm,此时辐射声压最大,随着间距的增大,振膜辐射声压逐渐降低.对于3×3阵元振膜,存在3类振膜(振膜5、6、7),不能通过其中一类振膜决定最佳间距值.假定振膜5、6、7振动速度相同,计算平均辐射阻抗曲线如图8所示,得到最佳间距为160,mm.同时计算4×4阵元3类振膜(振膜1、2、3)的辐射阻抗曲线,得到振膜最佳间距为130,mm.
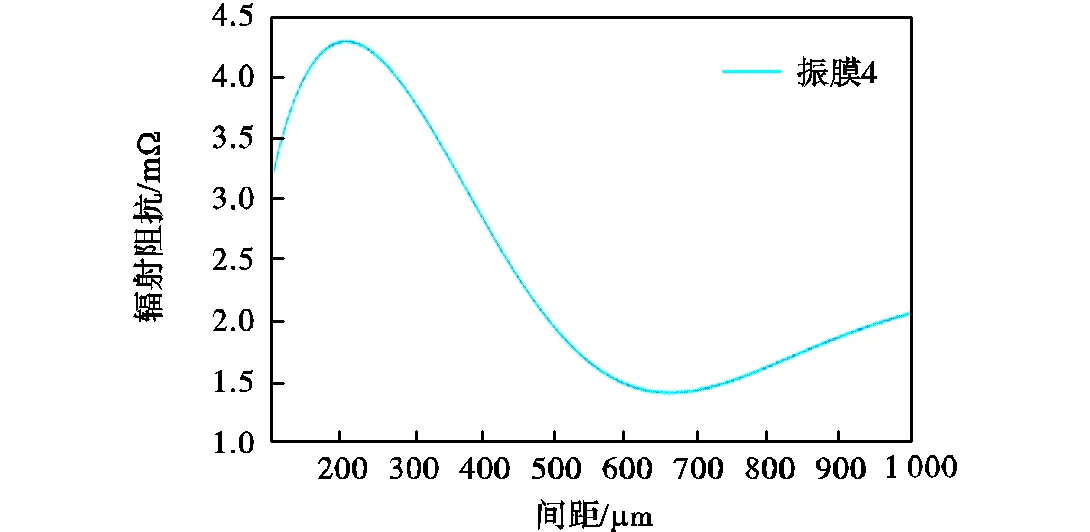
(a)2×2阵元振膜
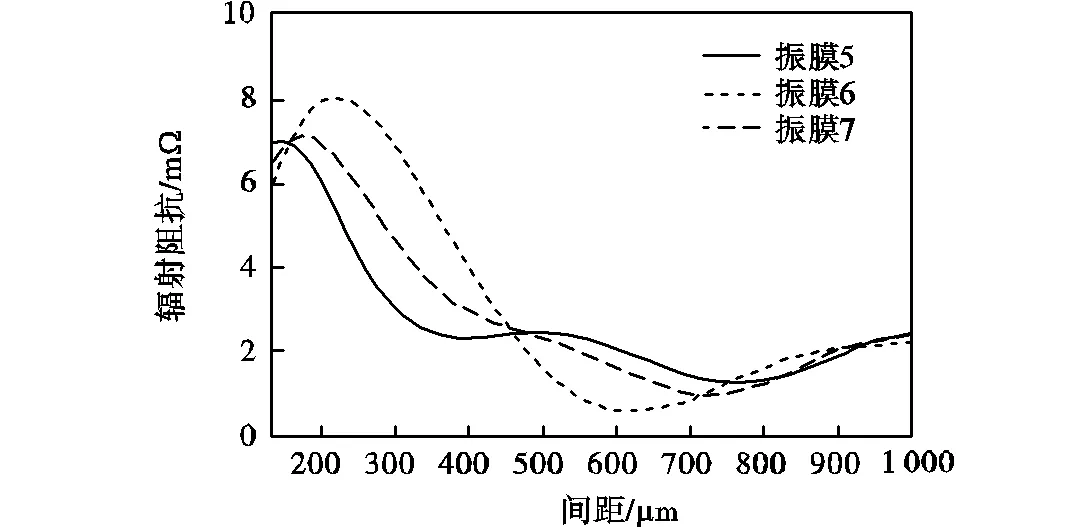
(b)3×3阵元振膜

(c)4×4阵元振膜
图7 阵元振膜辐射阻抗随间距变化曲线
Fig.7 Variation of cell membrane radiation impedancepitch
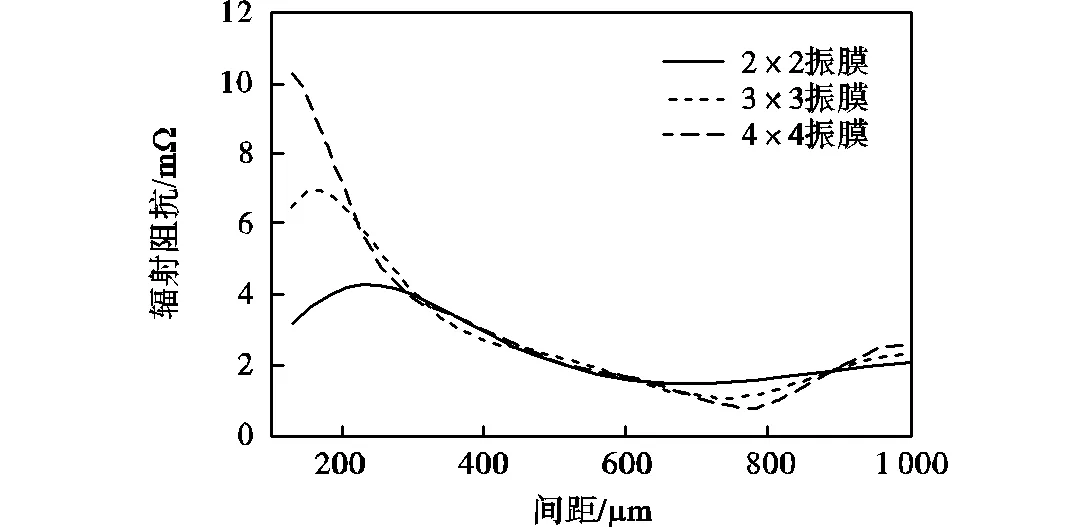
图8平均计算后不同规模阵元振膜辐射阻抗随间距变化曲线
Fig.8 Average radiation impedance of the cell membrane in three types of square array elementspitch
比较不同规模阵元振膜的阻抗变化曲线,发现阵元规模越大,阵列最佳间距越小,振膜的辐射阻抗越大,则振膜辐射声压越大.当阵元规模扩大到5×5时,振膜最佳间距等于振膜直径.实际受到加工工艺的限制,通常阵列的规模不大于4×4.设计中可以根据不同应用要求选取阵元的规模.
对于振膜半径为65,mm的3种规模阵元,振膜间距选取最优值,仿真得到振膜振动位移幅值与阵元机电电导率的频响曲线,如图9所示.由图9(e)、(a)、(c)可知振膜1~7优化后共振频率分别为1.63,MHz、1.56,MHz、1.49,MHz、1.82,MHz、1.72 MHz、1.68MHz、1.63,MHz,由图9(f)、(b)、(d)可知3种阵元取得最佳机电耦合效率的频率分别为1.62,MHz、1.85,MHz、1.76,MHz,在应用中,针对3种不同规模阵元,激励信号工作频率应做相应的调整.
比较图6与图9,可以发现经过优化后的4×4阵元3种振膜的振动幅度都有所增加,分别由37.5,nm、37,nm、34,nm提高到40,nm、42,nm、45,nm.但是振膜的共振频率降低,所以提高振膜辐射强度是以降低其共振频率作为代价的.对于环形阵列或二维阵列[16],可以采用4×4的多膜CMUT阵元,阵元间距选取最佳间距为130,mm,由图9(f)可知,激励信号中心频率可设为1.62,MHz.
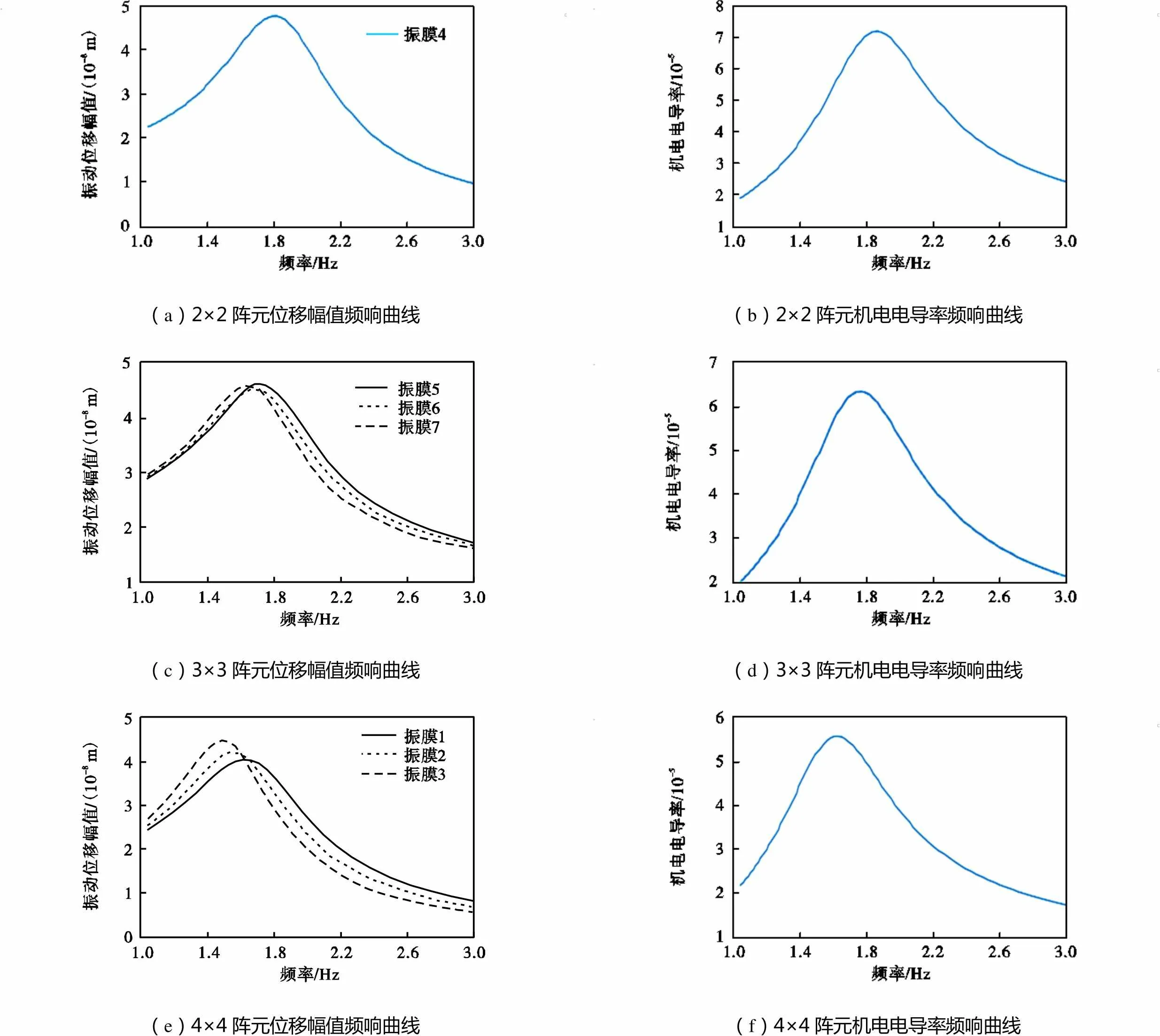
(a)2×2阵元位移幅值频响曲线(b)2×2阵元机电电导率频响曲线 (c)3×3阵元位移幅值频响曲线(d)3×3阵元机电电导率频响曲线 (e)4×4阵元位移幅值频响曲线(f)4×4阵元机电电导率频响曲线
4 结 语
本文将CMUT声学、力学参数等效成电学元器件,建立了非线性等效电路模型,利用该模型对方形排布的多膜CMUT阵元中的振膜进行仿真分析,得出了4×4阵元中振膜1~3的共振频率分别为1.84,MHz、1.81,MHz、1.72,MHz,并且通过多普勒测振系统对仿真结果进行了验证.应用模型优化设计多膜CMUT阵元,得到2×2、3×3与4×4这3种方形排布的阵元振膜的最佳间距分别为230,mm、160,mm与130,mm.完成优化后,得到3种阵元最佳工作频率分别为1.62,MHz、1.85,MHz、1.76,MHz,振膜振动的幅值有所增加,优化取得了明显的效果.
[1] Yaralioglu G,Ergun S,Khuri-Yakub B. Finite-element analysis of capacitive micromachined ultrasonic transducers[J].,2005,52(12):2185-2198.
[2] Ballandras S,Wilm M,Gelly J. Theoretical analysis of micromachined ultrasonic transducer using a simple 1-D model[J].,2006,53(1):209-223.
[3] Ahmad B,Pratap R. Elasto-electrostatic analysis of circular microplates used in capacitive micromachined ultrasonic transducers[J],2010,10(11):1767-1773.
[4] Mason W.[M]. New York:Van Nostrand,1948.
[5] Ladabaum I,Jin X,Soh H,et al. Surface micromachined capacitive ultrasonic transducers[J].,1998,45(3):678-690.
[6] Lohfink A,Eccardt P C. Linear and nonlinear equivalent circuit modeling of CMUTs[J].,2005,52(12):2163-2172.
[7] Koymen H,Senlik M,Atalar A,et al. Parametric linear modeling of circular CMUT membranes in vacuum[J].,2007,54(6):1229-1239.
[8] Oguz H K,Olcum S,Senlik M N,et al. Nonlinear modeling of an immersed transmitting capacitive micromachined ultrasonic transducer for harmonic balance analysis[J].,2010,57(2):438-447.
[9] 杜功焕,朱哲民,龚秀芬. 声学基础[M]. 南京:南京大学出版社,2012.
Du Gonghuan,Zhu Zhemin,Gong Xiufen.[M]. Nanjing:Nanjing University Press,2012 (in Chinese).
[10] Kagan-Oguz H,Olcum S,Senlik M N,et al. A novel equivalent circuit model for CMUTs[C]//. Rome,Italy,2009:2193-2196.
[11] Porter D T. Self-and mutual-radiation impedance and beam patterns for flexural disks in a rigid plane[J].,1964,36:1154-1161.
[12] Senlik M N,Olcum S,Koymen H,et al. Radiation impedance of an array of circular capacitive micromachined ultrasonic transducers[J].,2010,57(4):969-976.
[13] Sha K,Yang J,Gan W S. A simple calculation method for the self-and mutual-radiation impedance of flexible rectangular patches in a rigid infinite baffle[J].,2005,282(1/2):179-195.
[14] Caliano G,Caronti A,Baruzzi M,et al. Pspice modeling of capacitive microfabricated ultrasonic transducers [J].,2002,40(1/2/3/4/5/6/7/8):449-455.
[15] Yamaner F Y,Olcum S,Oguz H K,et al. Optimizing CMUT geometry for high power[C] //. San Diego,USA,2010:2247-2250.
[16] Yeh D T,Oralkan O,Wygant I O,et al. 3-D ultrasound imaging using a forward-looking CMUT ring array for intravascular/intracardiac applications[J].,2006,56(6):1202-1211.
(责任编辑:孙立华)
Equivalent Circuit Model and Element Optimization of CMUT
Zhang Hui1,Shi Jianchao1,Zhang Wen1,Zeng Zhoumo1,Qi Lei2
(1. State Key Laboratory of Precision Measurement Technology and Instruments,Tianjin University,Tianjin 300072,China;2. Beijing Institute of Spacecraft Environment Engineering,Beijing 100094,China)
A nonlinear equivalent circuit model for capacitive micromachined ultrasonic transducers(CMUT)was proposed.The equivalent circuit model is based on vibration surface motion equations,and the mechanical and acoustic parameters are equivalent to electricity components.It can be used to analyze both a single CMUT cell and CMUT cells in element.Considering acoustic interaction effects,the radiation impedance of CMUTs was accurately calculated and represented using an RLC circuit in the model.The frequency response of CMUT membrane vibration displacement amplitude was obtained by using SPICE simulation and the frequency response of cells located at different positions in one element was measured by Doppler vibrometer to verify the equivalent circuit model.Three types of elements are designed whose cells are arranged in 2×2,3×3 and 4×4 square array.The optimal pitch of cells in the three types of elements is 230,μm,160,μm and 130,μm respectively.
micro-electromechanical systems;capacitive micromachined ultrasonic transducers(CMUT);nonlinear equivalent circuit model;radiation impedance
10.11784/tdxbz201511007
TP212
A
0493-2137(2016)11-1209-07
2015-11-02;
2015-12-14.
国家自然科学基金资助项目(61201039);天津科技支撑计划资助项目(14ZCZDGX00003).
张 慧(1975— ),女,博士,副教授.
张 慧,hzhang@tju.edu.cn.
2016-01-22.
http://www.cnki.net/kcms/detail/12.1127.N.20160122.1033.006.html.

