轴向通风永磁同步电机三维热网络模型

李 斌，孙竟成，李 华



轴向通风永磁同步电机三维热网络模型

李 斌1，孙竟成1，李 华2

(1. 天津大学电气与自动化工程学院，天津300072；2. 国网辽宁省电力有限公司经济技术研究院，沈阳110015)

轴向通风电机中的冷却介质存在温差，直接影响电机的温度场分布．针对这一问题，建立了轴向通风永磁同步电机中冷却气流的数学模型，并与永磁同步电机本体结构的热网络模型相结合，构建了整体三维热网络模型．建立了描述导纳矩阵、网络节点温度、冷却气流温度之间关系的节点方程，得到了轴向非对称的温度分布，克服了传统T型网络法的不足．运用有限元软件进行流体场和温度场的耦合仿真，对比两者得出的温度值，证实了该三维热网络模型的可行性．

永磁同步电机；轴向通风；冷却气流；三维热网络；有限元法；耦合场

永磁同步电机与传统电励磁电机相比，具有结构简单、可靠性强、功率密度高等诸多优点，因而应用广泛．然而温度过高会导致永磁材料退磁，影响电机的效率、使用寿命和可靠性，所以温度场计算是永磁同步电机设计过程中必不可少的环节．

热网络法是计算电机温度场常用的方法，具有计算量小，耗时短的特点，该方法将电机温度场离散化为网格，将分布参数转换为集中参数，构成电机等效热网络，可根据电机的具体结构以及期望得到温度的部位灵活设置节点和热阻[1-3]．Mellor等[4]在建立电机热网络时，提出了T型等效热网络模型，该模型以固定的热路形式表示电机的各个部件，能实现轴向和径向的热流分析和温度计算．然而，建立T型网络时，通常假设电机轴向呈对称结构，忽略了冷却介质的轴向温差，认为电机温度以中间横截面呈对称分布，这在冷却介质轴向温差较大的电机中是不合理的[5-8]为解决电机中冷却介质在各部位存在温差的问题，文献[9]通过研究流场的流动和传热特性，设计了自循环蒸发冷却电机的热网络，网络中加入了热压源来表示冷却介质的温度．随着计算机技术不断发展，有限元法在电机的温度场计算中得到了广泛应用．为了模拟电机中的冷却介质对各部位温度的影响，得到更加精确的温度场分布，需要进行温度-流体耦合场分析[10]，然而其较大的运算负担增大了仿真时间，不利于电机的优化设计．

本文以文献[4]的T型等效网络为基本单元，考虑存在轴向通风冷却的情况，建立了永磁同步电机三维热网络模型，得到了轴向非对称的电机温度场分布，在此基础上运用有限元软件，进行了电机温度场和流体场耦合仿真，证实了该三维热网络模型的正确性和可行性．

1 永磁同步电机热网络模型

1.1 T型等效热网络法

传导热阻的计算公式为

   (1)

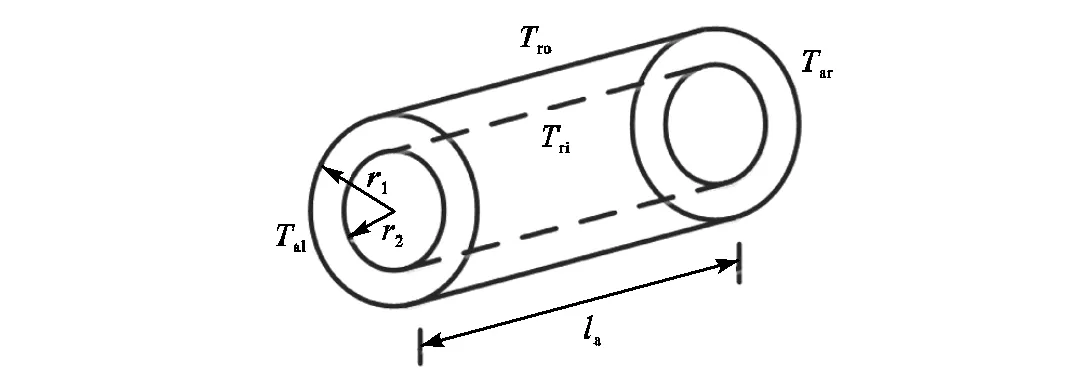
电机的定子轭、永磁体、转子轭均为如图1(a)所示的圆环柱体，图中为轴向长度，1和2分别是对应圆环柱体的外径和内径，al和ar分别为轴向两个端面的温度，ri和ro分别为内环和外环表面的温度，假设该圆环柱体轴向和径向的导热相互独立，且不存在环向热流，可将圆环柱体分布参数模型简化成T型集中参数模型，如图1(b)所示，其中，m为整个柱体的平均温度，为该柱体的生热功率．由式(1)可得6个热阻计算公式分别为

 (2)

式中r和a分别为圆环柱体径向和轴向的热导率，W/(m·K)．

（a）圆环柱体结构

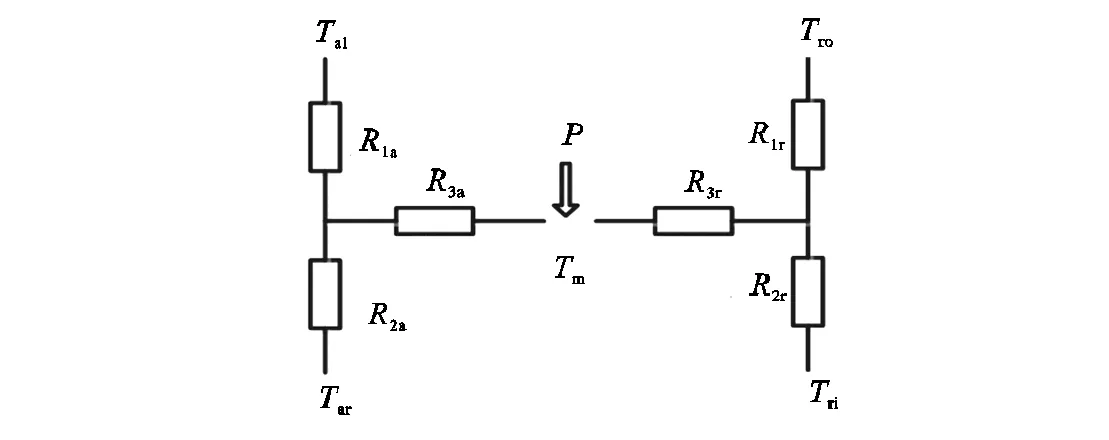
（b）T型等效热网络

图1 圆环柱体结构及T型等效热网络

Fig.1 Cylindrical structure and T-type equivalent thermal network

利用等效横截面积法[11]，定子齿和定子绕组也可转换成圆环柱体结构．应用式(2)，即可建立各自的T型热网络模型．

1.2 网络中的对流热阻

对流热阻的计算公式为

   (3)

对流换热系数的确定是计算对流热阻的关键. 永磁同步电机的结构比较复杂，常用经验公式法来确定其定转子间气隙、外壳和端部3个部位的对流换热系数．

定转子间气隙的对流换热系数计算式为

   (4)

电机端部的对流换热系数计算式[11]为

   (5)

电机外壳与外界的对流换热系数计算式[13]为

   (6)

2 三维热网络模型的实现

由第1节建立的电机各个部件的T型等效网络相互连接，可以建立整个电机的热网络．然而问题是T型等效网络的对称性决定了最终求得的电机两个端面的温度相等，各个部位的温度最高点在中间的横截面上，本文所研究的电机设有轴向通风冷却结构，电机两个端面的温度必然存在差异，高温一侧有可能因此而局部过热，所以在建立模型时，必须充分考虑冷却系统对电机温度的影响．本节建立了流通在电机内部冷却气流的数学模型，该模型可以与热网络构成一个整体，在一个方程组中同时求解，最终建立了轴向通风永磁同步电机的三维热网络模型．

2.1 冷却通风系统模型建立

冷却气流可以模拟为由冷却气流量控制的热压源[9,14]，与电路中的流控电压源形成类比．图2给出了永磁同步电机中冷却气流温升示意，假设气流温度在端部和转子通风孔内呈线性变化，因此把各自中点位置的温度视为气流的平均温度．

图2 永磁同步电机中冷却气流温升示意

冷却气流从电机一侧端部流入，吸收掉绕组端部由定子轭、绕组端部、转子轭和永磁体通过热对流散发的热功率ec1，使气流温度升高，温升为

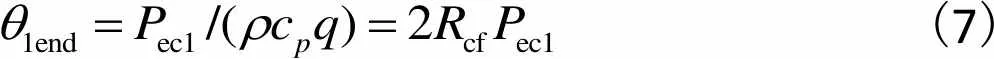
   (7)

   (8)

式中：cf为热阻的量纲；为气体密度，kg/m3；为气体比定压热容，J/(kg· K)；为气体流量，m3/s.

各部位温度呈线性上升，低温一侧气体平均温 升为

   (9)

   (10)

将式(7)和式(8)代入式(10)中，得

   (11)

   (12)

   (13)

式中ec2为冷却气流在高温一侧端部吸收的由定子轭、绕组端部、转子轭和永磁体通过热对流散发的热功率．

冷却通风系统建立如上所述，用3个节点来表示冷却气流．类似于电路中的流控电压源，这里的冷却气流表示为气体流量控制的位于3个节点的热压源．

2.2 三维热网络模型

得到了3个热压源的表达式，可以建立完整的永磁同步电机三维热网络模型，如图3所示．

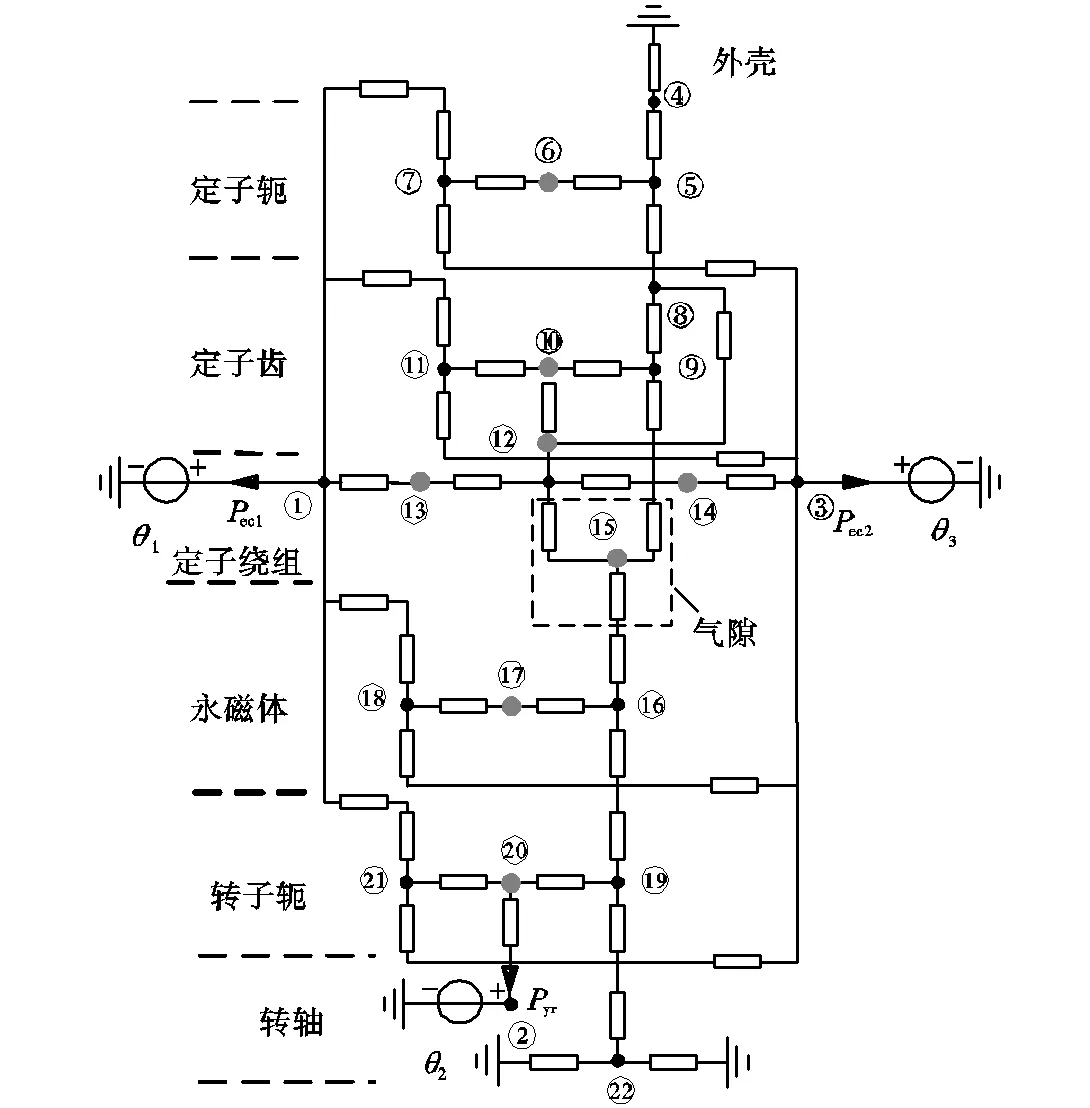
图3 永磁同步电机三维热网络模型

图中节点①、③分别表示电机两侧端部气体平均温度点，节点②表示转子通风孔中气体的平均温度点，灰色节点为电机各个部位的损耗注入节点，节点⑥表示定子轭铁耗，节点⑩表示定子齿铁耗，节点⑫表示定子绕组铜耗，节点⑬和⑭表示绕组端部铜耗，节点⑮表示气隙摩擦损耗，节点⑰表示永磁体涡流损耗，节点⑳表示转子轭涡流损耗，其余节点既无热流注入，也未与热压源连接．图中灰色节点为该部位注入的热功率数值，黑色节点没有功率注入，其值均为0．网络中有、、3个热压源，代表图2中冷却气流的平均温升，通过一个对流热阻与转子轭平均温度节点⑳相连．为了完善热网络模型，网络中额外定义了一些热阻模拟各部位的接触热阻和对流热阻．

求解网络时要注意，加入冷却气流的热网络模型中存在热压源，方程形式为

   (14)

热导纳矩阵的表达式为

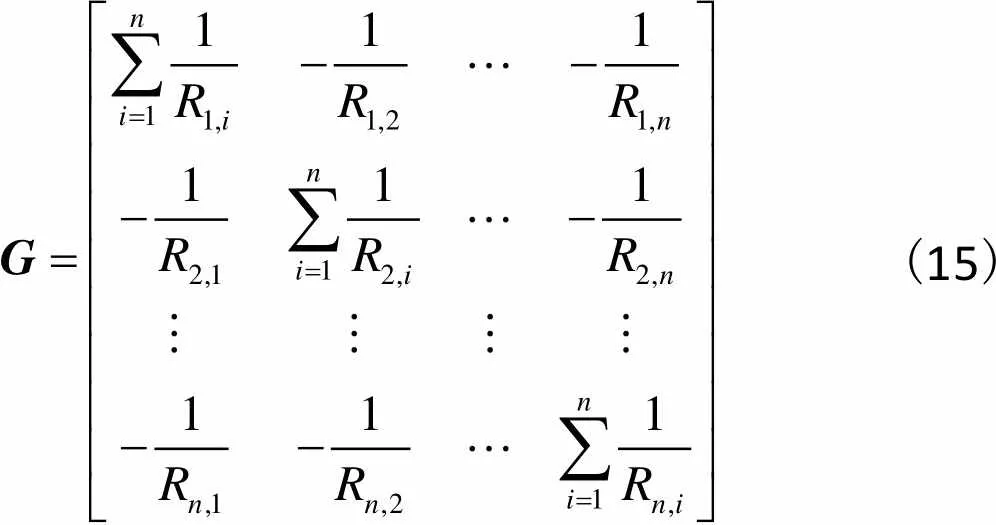
   (15)

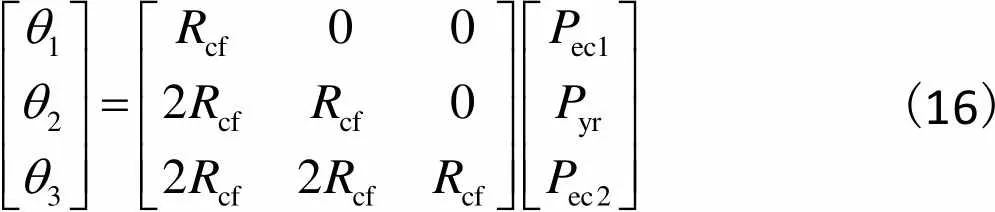
   (16)

简写为

   (17)

将式(17)代入式(14)中，得

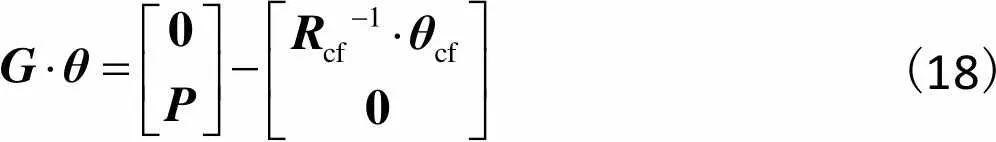
   (18)

移项并合并同类项得到热网络各节点的温升

   (19)

本节建立的三维热网络模型具有如下特点：

(1)电机自身结构形成的无源热网络与通风系统冷却气流形成一个整体，能在同一方程组中求解；

(2)模型针对电机内部主要部件的温度进行计算，省略了外壳、端盖与轴承之间复杂的热连接，建模和计算较简单．

3 温度场仿真与结果分析

3.1 仿真结果分析

电机模型为3,000,r/min，2对极，表贴式永磁同步电机，转子设有轴向通风孔，存在轴向冷却通风系统．仿真过程中做如下假设：冷却气流仅从转子通风孔内流入流出，不经过定转子间气隙，电机中各部件产生的热量均匀地分布于固体之中且忽略气隙风摩擦损耗，表1为各部位施加的热载荷．

表1 各部件施加的热载荷

Tab.1 Thermal load of components

建立转子流体-温度耦合场，取电机1/8建立模型，仿真过程中，使转子静止，冷却气流以切向速度8,m/s和轴向速度6,m/s叠加进入通风孔，以此来模拟转子旋转的实际情况．图4为转子通风孔内气体流速矢量图，图中右侧为入口处流速矢量的放大图．图5为转子通风孔内冷却气流的温度分布．将流体场中得到的通风孔壁面对流散热系数的分布结果导入到温度场分析系统中，作为温度场分析的边界条件．

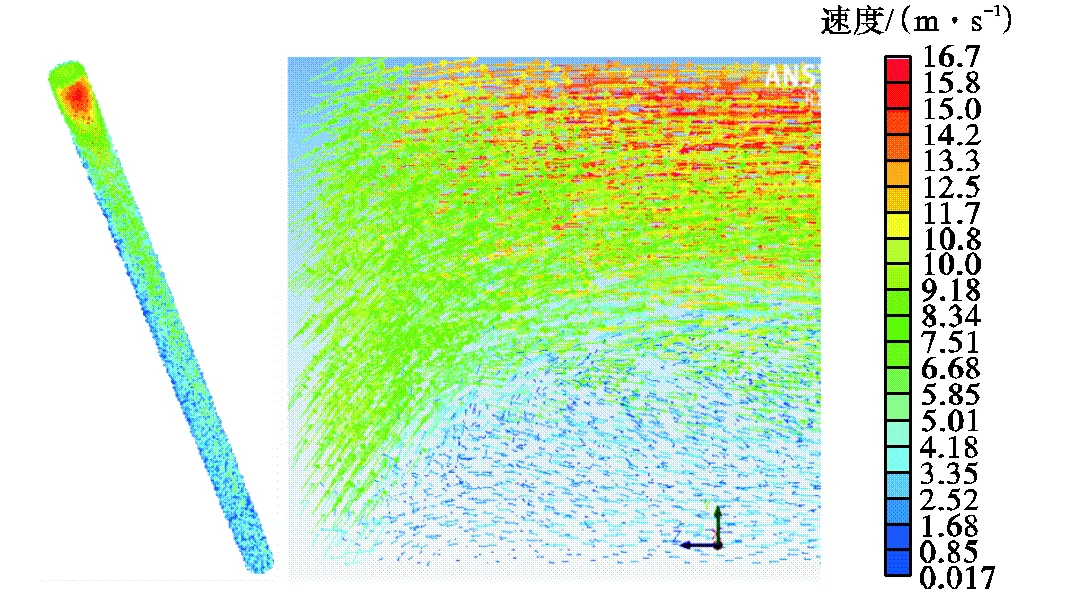
图4 通风孔内气体流速矢量图

图5 通风孔内冷却气流温度分布

图6为转子的温度分布，图6(a)没有施加冷却通风的边界条件，图6(b)为施加后的温度分布．可见，通风孔中的冷却气流不仅大幅降低了转子的温度，对永磁体起到了很好的保护作用，而且使转子温度峰值点向气流出口侧推进．

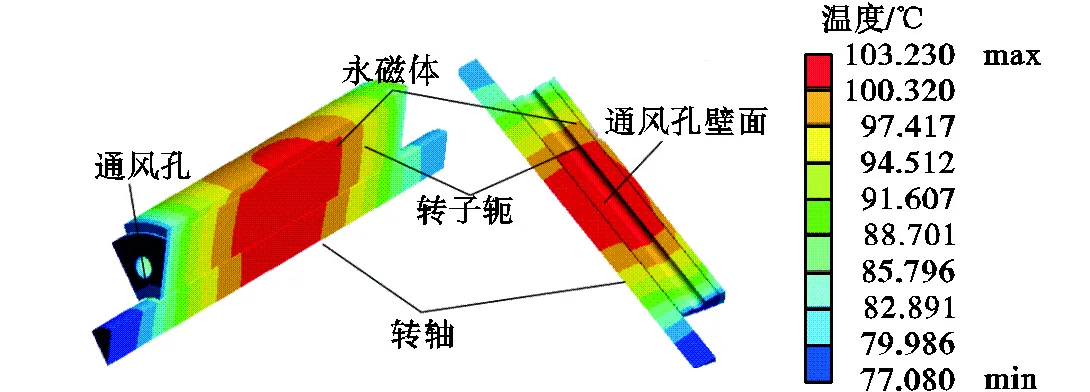
（a）无冷却

（b）有冷却

图6 有无冷却气流转子温度分布

Fig.6 Temperature distribution of rotor with or with-out cooling air flow

进行定子温度场仿真时，将在流体场中得到的入口和出口处气流的平均温度29.4,℃和41.3,℃作为边界条件．得到如图7所示的温度场分布，给出了轴向和径向截面的温度分布．

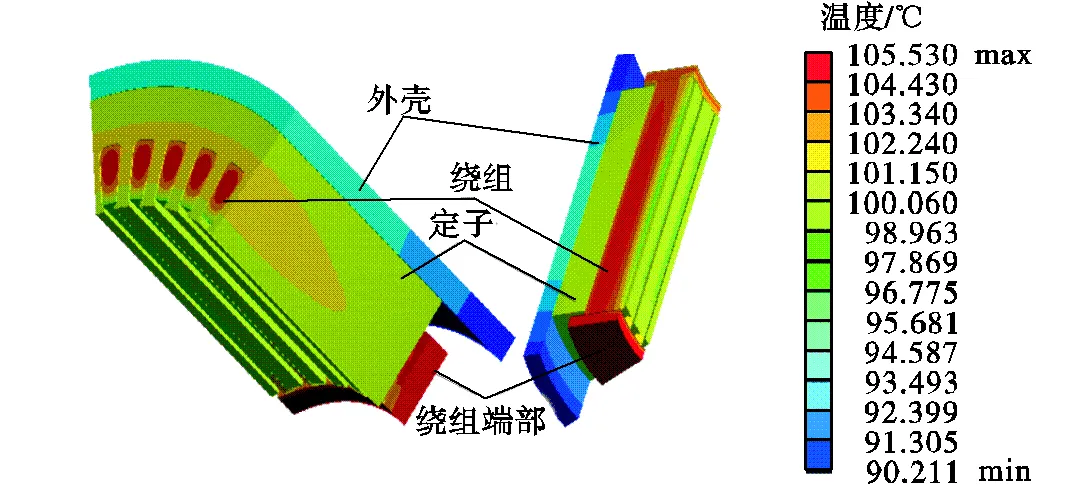
图7 电机定子温度分布

3.2 结果对比分析

运用第2节中的方法求解三维热网络模型，取参考节点温度为20,℃，得到各节点的温度如表2所示．

表2 热网络节点温度

Tab.2 Temperature of thermal network nodes

结果显示存在轴向通风冷却系统的情况下，永磁体和转子的温度比定子低很多，从前面温度分布也可得出该结论．图8为电机各部位有限元仿真温度最大值、最小值与热网络求解结果对比，可以看出网络计算结果与仿真值比较接近，很好地证明了冷却通风系统模型以及整个三维热网络模型的可行性．

图8 仿真与网络求解结果对比

在进行上述仿真时，计算机处理器为i5-4590，内存为8G．在等效热网络分析时，利用Matlab软件计算所有热阻阻值并求解网络矩阵，得到各节点温升，整个过程仅用时5,s．而在有限元分析中，模型剖分节点数为222,974，单元数为43,563，得到定转子温度分布共用时85,min，可见该三维热网络模型可大大降低运算负担，有利于电机优化设计．

4 结 语

本文以传热学原理为基础，对轴向冷却系统的冷却气流进行了数学建模，将其与热网络结合成一个整体，构成轴向通风永磁同步电机的三维等效热网络，得到了3个位置冷却气流的平均温升，两侧端部气流温度相差19,℃，使网络中各节点温度轴向非对称分布；通过有限元软件进行流体-温度耦合场仿真，得到结果与网络计算值比较接近，很好地证明了该三维热网络模型的可行性，可以在电机的优化设计过程中提供一些帮助．

［1］ Gerada D，Mebarki A，Mokhadkar R P，et al. Design issues of high-speed permanent magnet machines for high-temperature applications[C]//. Miami，FL，USA，2009：1036-1042.

［2］ Wang W，Zhou Y，Chen Y. Investigation of lumped-parameter thermal model and thermal parameters test for IPMSM[C]//17()Hangzhou，China，2014：3246-3252.

［3］ 程树康，李翠萍，柴 凤. 不同冷却结构的微型电动车用感应电机三维稳态温度场分析[J]. 中国电机工程学报，2012，32(30)：82-90.

Cheng Shukang，Li Cuiping，Chai Feng. Analysis of the 3D steady temperature field of induction motors with different colling structures in mini electric vehicles[J].，2012，32(30)：82-90(in Chinese).

［4］ Mellor P H，Roberts D，Turner D R. Lumped parameter thermal model for electrical machines of TEFC design[J].，1991，138(5)：205-218.

［5］ Boglietti A，Cavagnino A，Lazzari M. A simplified thermal model for variable-speed self-cooled industrial induction motor[J].，2003，39(4)：945-952.

［6］ Rostami N，Feyzi M R，Pyrhonen J，et al. Lumped-parameter thermal model for axial flux permanent magnet machines[J].2013，49(49)：1178-1184.

［7］ Jiang T，Liu G，Zhou H. Simplified thermal modeling of fault-tolerant permanent-magnet motor by using lumped parameter network[C]//()，. Beijing，China，2014：1-4.

［8］ Kim K S，Lee B H，Kim H J，et al. Thermal analysis of outer rotor type IPMSM using thermal equivalent circuit[C]//15Sapporo，Japan，2012：1-4.

［9］ 刘长红，姚若萍. 自循环蒸发冷却电机定子铁心与绕组间的热量传递[J]. 中国电机工程学报，2008，28(11)：107-112.

Liu Changhong，Yao Ruoping. Heat transfer between stator core and windings in hydro-generators with self pump circulated evaporation cooling system[J].2008，28(11)：107-112(in Chinese).

［10］ Xu Z，Tighe C，Galea M，et al. Thermal design of a permanent magnetic motor for direct drive wheel actuator[C]//()Berlin，Germany，2014：2186-2192.

［11］ Roberts D. The Application of an Induction Motor Thermal Model to Motor Protection and Other Functions[D]. Liverpool：University of Liverpool，1986.

［12］ Luke G E. The cooling of electric machines[J].，1923，42(12)：636-652.

［13］ 黄国治，傅丰礼. 中小旋转电机设计手册[M]. 北京：中国电力出版社，2014.

Huang Guozhi，Fu Fengli.[M]. Beijing：China Electric Power Press，2014 (in Chinese).

［14］ Pyrhonen J，Jokinen T，Hrabovcova V.[M]. Finland：Wiley & Sons，2013.

（责任编辑：孙立华）

Three Dimensional Thermal Network Model of Permanent Magnet Synchronous Machine Equipped with Axial Ventilation System

Li Bin1，Sun Jingcheng1，Li Hua2

(1．School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China；2．State Grid Liaoning Electric Power Supply Corporation Limited Economic Research Institute，Shenyang 110015，China)

The temperature difference in cooling medium has influence on the thermal distribution in the electrical machine．To solve this problem，the mathematical model of the coolant air flow in the permanent magnet synchronous machine(PMSM)equipped with axial ventilation system is built．The 3D thermal network model is constituted by combining the thermal network model of the machine body and the model of the coolant air flow．The node equation is established to describe the relations among admittance matrix，temperature of network nodes and the coolant air flow．Then asymmetrical temperature distribution in the axial direction is obtained，which overcomes the shortage of the traditional T-type equivalent network．Meanwhile，the coupling of fluid field and thermal field simulation is implemented using finite element method(FEM)software．The feasibility of the proposed 3D thermal network model is verified by comparing the results of the thermal model and the FEM simulation.

permanent magnet synchronous machine(PMSM)；axial ventilation；coolant air flow；3D thermal network；finite element method；coupling field

10.11784/tdxbz201603066

TM351

A

0493-2137(2016)11-1161-06

2016-03-23；

2016-06-28.

国家自然科学基金资助项目(51577125).

李 斌（1976—  ），男，博士，副教授，elib@tju.edu.cn.

孙竟成，jcsun@tju.edu.cn