基于Ritz级数法滚珠丝杠的混合模型研究*
王 娜,姜宝华*,宗成国
(1.青岛黄海学院 智能制造学院,山东 青岛 266427;2.山东科技大学 机械电子工程学院,山东 青岛 266590)
0 引 言
目前,滚珠丝杠广泛应用于数控机床的进给系统中。然而当系统加速度较高时,进给系统会产生振动,影响机床的加工质量及精度。因此,研究丝杆传动系统的建模,并对系统提出有效的补偿尤为重要。
常用建模方法中,集中参数法相对简单,但不能完整表达系统振动特性;有限元法较为全面但模型复杂,所含矩阵计算量大。
近年来,混合模型法的研究受到了业界的广泛关注。OKWUDIRE等[1]使用混合模型方法,得出了包含轴向、扭转及弯曲向的丝杆刚度矩阵。VICENTE等[2]通过Ritz级数法,对丝杆传动系统的轴向、扭转振动进行了建模。PISLARU等[3]通过混合模型,并考虑滚珠丝杠的分布力、阻尼以及摩擦和间隙等特性,通过仿真得到了与实验结果大体一致的结果。张会端等[4]将系统中的丝杆简化为旋转Timoshenko梁,全面地考虑了移动力、预拉伸力及陀螺效应等因素对滚珠丝杠振动模态的影响,设定丝杠两端均为为弹性支撑,推导出了丝杆的振动方程,在改变系统参数的情况下对丝杆弯曲振动模态的变化进行了分析,但缺乏对丝杆的轴向及扭转振动模态的研究,并且没有进行实验验证。目前,该领域的研究大多忽略丝杠的弯曲振动,并且关于工作台和丝杆的参数变化对丝杆振动影响的理论和实验研究很少。
笔者提出一种高速滚珠丝杠传动系统的混合模型方法,通过建立连续体模型来描述该系统的振动特性,以及丝杆在承受移动载荷时的动力学特性。
1 滚珠丝杠系统力学分析及建模
滚珠丝杠传动系统结构示意图如图1所示。
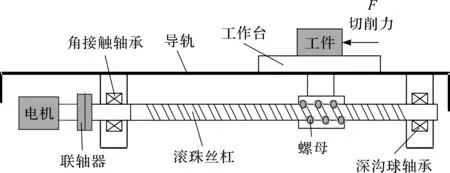
图1 滚珠丝杠传动系统示意图
图1中,该系统采用了单边支撑法,伺服电机与滚珠丝杠由联轴器连接,使得电机可以带动丝杆旋转,丝杠两端分别由两个不同轴承与机架固定,近电机端为角接触轴承,另一端为深沟球轴承。该方法可避免双边支撑结构因热变形从而产生的应力,因而被广泛应用于精密丝杆的驱动系统中。丝杆的进给系统3种振动模态分别为:轴向、扭转和弯曲。
为了满足丝杠伺服系统在高速进给状态下的高精度要求,电机处装有旋转编码器用于反馈旋转位置,光栅尺用于反馈工作台的位置;低阶,特别是一阶的轴向和扭转振动模态对于控制器的稳定性有很大影响。
滚珠丝杠传动系统的受力分析模型如图2所示。
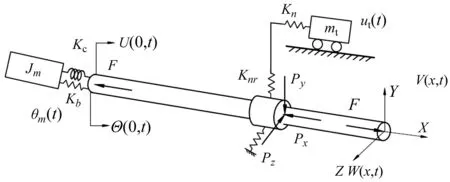
图2 滚珠丝杠传动系统受力分析模型
图2中,丝杠部分简化为Timoshenko梁,其他构件用刚度来表示,除丝杆的轴向和扭转振动之外,还考虑了弯曲振动。
模型参数含义简介如表1所示。

表1 模型参数含义简介
1.1 建模
Ritz级数法是通过级数的展开式来描述位移x的依赖性,级数的系数为时间t的函数,t未知。以功率平衡为基础对系统进行理论建模,可导出描述质量、刚度、阻尼的矩阵和广义力。
公式参数含义简介如表2所示。

表2 公式参数含义简介
1.1.1 轴扭耦合振动模型
使用Ritz级数描述丝杠的轴向位移和扭转位移如下:
(1)
两个方向的振动通过丝杠螺母耦合,δn表达式为:
(2)
总动能T表达式为:
(3)
将Ritz表达式代入式(3)中,写为矩阵:
(4)
势能U表达式为:
(5)
将Ritz表达式带入式(5)中,写为矩阵:
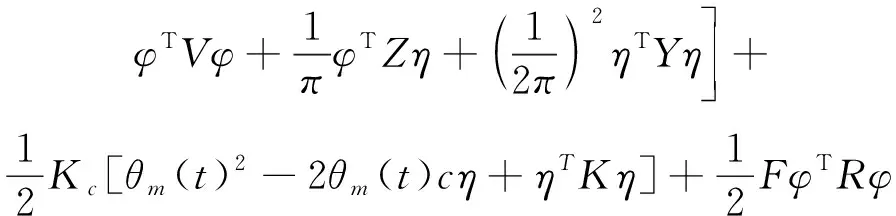
(6)
式中:Px—虚功,δW=PxδU(s(t),t);L—拉格朗日量,L=T-U+δW。
推导出系统的运动方程为:
(7)
系统的广义坐标定义为:Δ={φTutηTθm}T
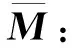
(8)

(9)
综合考虑滚珠丝杠副的内部功耗,以及其他构件阻尼,可得Pdis表达式:
(10)
(11)
力Pin表达式为:
(12)
矩阵Q为:
(13)
1.1.2 弯曲振动模型
将滚珠丝杠副系统视为沿轴旋转对称系统,丝杆视为Timoshenko梁。将两端轴承视为刚体,使用Ritz级数描述系统横向变形和转角,即:
(14)
综合考虑转角以及位移的关系,Uf可写为:

(15)
将基函数代入式(15),并写为矩阵:
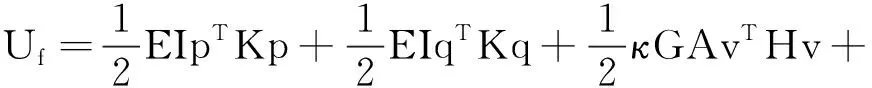
(16)
动能Tf表达式可写为:
(17)
将其代入基函数,并写为矩阵:
(18)
螺母滚珠动能表达式可写成:
Tm=
(19)
将其代入基函数,并写为矩阵:
(20)
考虑mb,外力的虚功表达式为:
δW=mbgδV(xt,t)
(21)
将式(21)代入拉格朗日方程,则滚珠丝杠进给系统的弯曲运动方程可以表示为:
(22)
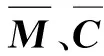
(23)
(24)

(25)
由于轴承的阻尼是系统功率消耗的主要原因,可得Pdis表达式为:
(26)

(27)
1.2 边界条件及基函数的选择
根据Ritz级数的原理,基函数需符合3个条件[5]:(1)线性独立;(2)位移函数连续;(3)符合丝杠系统在物理定义上的边界条件。若刚体可以运动,则相关基函数为Φ1=1。
1.2.1 轴向及扭转基函数的选择

1.2.2 弯曲基函数的选择
丝杠弯曲所承受的外界载荷由两部分构成[6-7],即作用于横截面的剪力和弯矩。在进行计算时,为避免约束力被纳入输入功率,对系统设定如下边界条件:Φj=0,dΦj/dx=0,并分别施加于不允许发生位移与扭转的位置。
在滚珠丝杠系统中,深沟球轴承为简支,角接触轴承为固定支撑。
(1)固定—简支。其物理边界条件表达式如下所示:
V(0,t)=V(L,t)=0;W(0,t)=W(L,t)=0
V′(0,t)=B′(L,t)=0;W′(0,t)=Γ′(L,t)=0
(28)
可得基函数为:
(29)
以此类推,即可得到其他支撑方式的结果。
(2)固定—固定。其物理边界条件表达式如下所示:
(30)
(3)简支—简支。其物理边界条件表达式如下所示:
(31)
1.2.3Ritz级数长度M的确定
使用Ritz级数法时[8],当M→∞时,各阶模态的固有频率无限接近其系统值。其中,M的3-10级数下,不同频率的仿真结果如表3所示。

表3 M的3-10级数下不同频率仿真结果
表3列出了不同M值的数值仿真结果(工作台位于xt=L/2处)。从不同长度仿真结果可知:振动频率随级数长度收敛,级数长度10是比较合适的选择。
2 实验验证
为了验证该模型的正确性,笔者进行了实验。实验验证所使用的设备如图3所示。

图3 实验验证设备
图3中,通过测试4个分散的滚珠丝杠系统中螺母的振动模态,即可验证工作台位置的改变与系统振动模态变化的关系;采用力锤为振动源,加速度传感器排布在工作台上,通过信号分析仪计算系统频响;12个测量参考点平均分布于丝杠,通过移动力锤改变振动源,实现对弯曲振动(径向振动)的测量。
模型验证设备主要参数如表4所示。
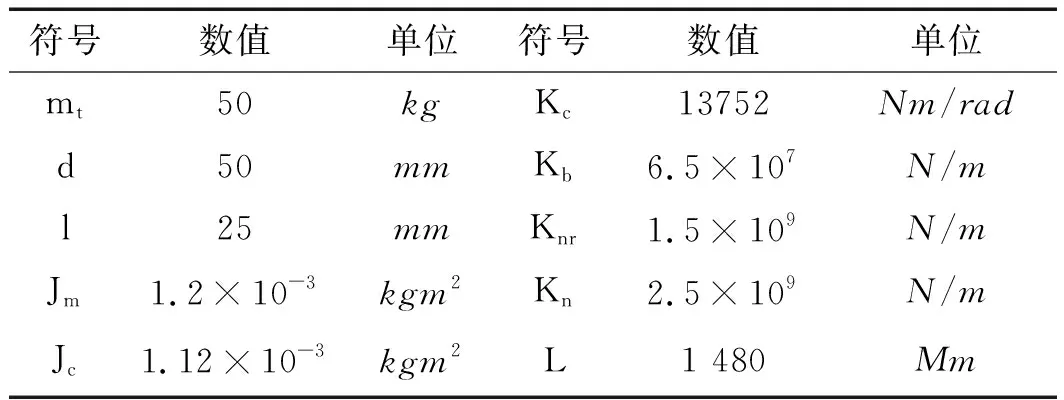
表4 模型验证设备主要参数
800 mm位置处频率的响应曲线如图4所示。

图4 800 mm位置处频率响应曲线
振动频率的实验及仿真结果如表5所示。
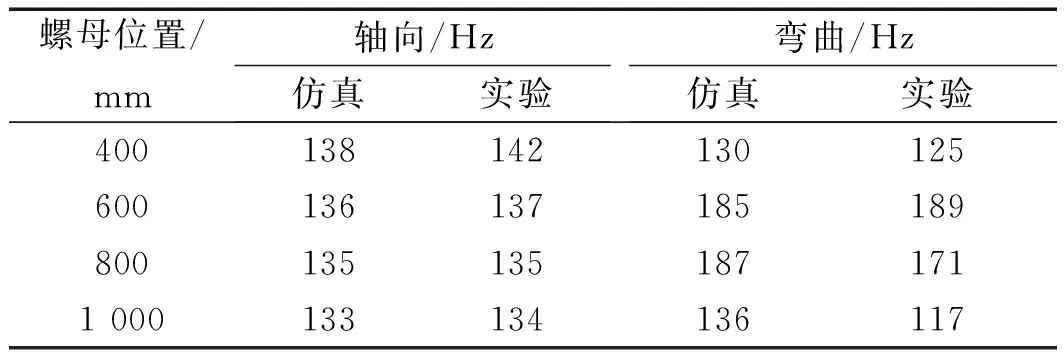
表5 振动频率的实验及仿真结果
对扭转振动的验证需参考文献[9]中所做的实验,通过笔者所建立模型仿真结果与上述文献所得的实验结果进行对比可知:一阶振动结果分别为424 Hz和434 Hz,二阶振动结果分别为1 369 Hz和1 120 Hz。
模型仿真与实验验证结果的对比图如图5所示。
由图5可知,模型仿真的结果与实验验证所得振型基本一致。
综上所述:经过实验验证对比,笔者所建模型可准确地描述滚珠丝杆传动系统的动力学特性,并对该系统的振动模态进行计算。

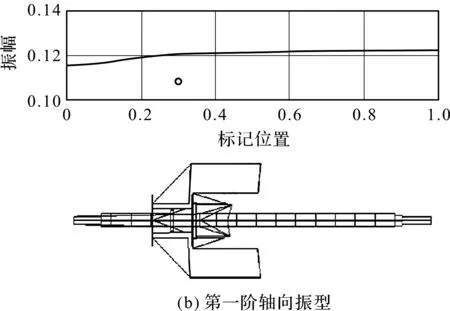
图5 数值仿真(上)与实验结果(下)对比
3 振动特性分析
3.1 随加工过程变化的振动分析
由于工作台属性参数的改变会对系统的振动模态产生影响[10],不同工作台位置xt的振型如图6所示。

图6 不同工作台位置xt的振型
由图6可得:工作台位置的变化对轴向振动影响较大,对于扭转振动影响较小。第一阶振动的轴向频率易受影响,第二阶振动的扭转频率易受影响,第三阶振动几乎不受影响。
3.2 不同导程的轴扭耦合振动的耦合情况
两种不同重量的工作台在丝杆的导程不同时,反映了振动频率的变化。不同导程对轴扭耦合振动的影响如表6所示。
由表6可知:重量较大的工作台的振动频率对于导程的变化更为敏感,并且对一阶影响更大;一阶时滚珠丝杆的导程大小与其传动系统的轴扭耦合度正相关,二、三阶为负相关。

表6 不同导程对轴扭耦合振动的影响xt=0.6 m
因此,在滚珠丝杆系统中,丝杆导程较大以及工作台较重时,轴扭耦合是不可或缺的一项。
4 结束语
基于Ritz级数法采用混合模型法,笔者综合考虑了轴扭耦合以及弯曲振动对系统的影响,对高速滚珠丝杠传动系统进行了建模;经过仿真与实验,对模型进行了验证,分析了丝杠导程、工作台参数等因素对丝杆系统振动模态的影响。
研究表明:轴向振动受工作台位置和质量因素影响较大,扭转振动所受影响较小;弯曲振动方面受工作台位置因素影响较大;随着工作台重量增加,工作台的振动频率对于丝杠导程的变化更为敏感。
笔者所建模型可以完整表达系统的振动特性,且系统的理论模型相对简单。

